20.已知数列的前项和和通项满足(是常数,且).

(1)求证:数列是等比数列；

(2) 若，求数列的前项和；

(3)若,设，是否存在正整数m，使 对一切都成立？若存在，求出的值，若不存在，说明理由.

宿迁市马陵中学09-10学年高二上学期期中考试

19．设为实数，函数．

(1)若，求的取值范围；

(2)求关于的不等式的解集．

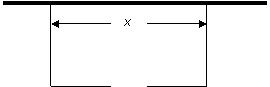
18．围建一个面积为360m²的矩形场地，要求矩形场地的一面利用旧墙(利用的旧墙需维修)，其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙长度为(单位：m)，修建此矩形场地围墙的总费用为y(单位：元) ．

(1)将y表示为的函数；

(2)试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用．

17．在ABC中，角A，B，C的对边分别为a，b，c，角．

(1)若a=2b，求角A，B；

(2)若c=2，求ABC周长的最大值．

16．已知是一个等差数列，且，．

(1)求数列的通项；

(2)求数列前n项和S_n的最大值．

15．在ABC中，角A，B，C的对边分别为a，b，c，且．

(1)求角的大小；

(2)若，且，求三角形ABC的面积．

14．如图甲是第七届国际数学教育大会(简称ICME－7)的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中，如果把图乙中的直角三角形继续作下去，记的长度构成数列，则此数列的通项公式为=　 ★　　 ．

13．观察　　 1

　　　　　 1+2+1

　　　　 1+2+3+2+1

1+2+3+4+3+2+1

……

则第行的值为　 ★　　 ．

12．已知三数，1，成等比数列，且，则的最小值是　 ★　　 ．

11．若实数满足则的最大值为　 ★　　 ．