
20.(16分)自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及其捕捞强度对鱼群总量的影响。用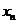 表示某鱼群在第
表示某鱼群在第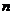 年年初的总量,
年年初的总量,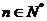 且
且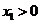 ,不考虑其他因素,设在第
,不考虑其他因素,设在第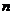 年内鱼群的繁殖量及其捕捞量都与
年内鱼群的繁殖量及其捕捞量都与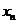 成正比,死亡量与
成正比,死亡量与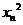 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数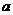 ,
,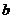 ,
,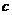 。
。
(1)求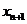 与
与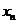 的关系式;
的关系式;
(2)猜测:当且仅当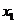 ,
,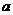 ,
,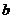 ,
,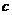 满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
19.(16分)在△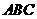 中,角
中,角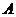 ,
,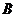 ,
,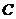 所对的边分别为
所对的边分别为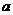 ,
,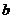 ,
,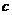 ,且
,且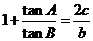 。
。
(1)求角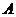
(2)若 ,
,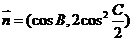 试求
试求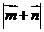 的最小值
的最小值
18.(16分)已知数列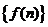 的前
的前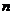 项的和为
项的和为 ,且
,且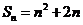
(1)求数列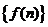 的通项公式;
的通项公式;
(2)若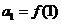 ,
,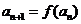 ,求证数列
,求证数列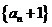 是等比数列,并求数列
是等比数列,并求数列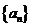 的前项和
的前项和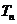 。
。
17.(14分)已知平面区域 被圆
被圆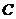 及其内部覆盖。
及其内部覆盖。
(1)当圆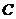 的面积最小时,求圆
的面积最小时,求圆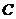 的方程
的方程
(2)若斜率为1的直线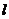 与(1)中的圆
与(1)中的圆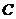 交与不同的两点
交与不同的两点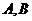 ,且满足
,且满足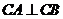 ,求直线
,求直线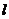 的方程
的方程
16. (14分)已知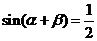 ,
,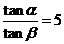 ,求
,求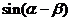 的值
的值
15.(14分)设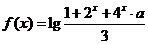 ,如果
,如果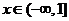 时
时 有意义,求实数
有意义,求实数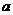 的取值范围。
的取值范围。
14.由曲线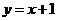 上的点向圆
上的点向圆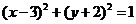 引切线,则切线长的最小值为 。
引切线,则切线长的最小值为 。
二 解答题(六大题共90分,把解答过程写到答案卷上)
13.已知实数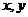 满足
满足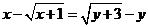 ,则
,则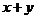 得最大值为 。
得最大值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com