4、在1molP原子形成的白磷中含有P-P键为(N_A为阿氏常数)

A、3N_A　 B、1.5 N_A　　 C　 4 N_A　 D 0.25 N_A

3、以下性质的比较中，不正确的是

A、晶格能 NaCl〈 MgO

B、熔点：NH₃ 〈 PH₃

C、离子半径：Na⁺〈 O^2-

D、第一电离能：Mg 〉Al

2、下列四种分子中中心原子杂化类型与三个不同的是

A、CH₄　　 B、NH₃　 C、H₂O 　　D、BF₃

1、下列说法正确的是

A、晶体在受热熔化过程中一定存在化学键的断裂

B、原子晶体的原子间只存在共价键，而分子晶体内只存在范德华力。

C、区分晶体和非晶体最科学的方法是对固体进行X-射线衍射实验

D、非金属元素的原子间只形成共价键，金属元素的原子非金属元素的原子间只形成离子键。

25.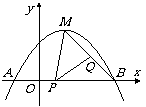 (本题满分12分) 如图，拋物线y₁=ax²-2ax+b经过A(-1，0)，

　 C(2，)两点，与x轴交于另一点B；

　 (1) 求此拋物线的解析式；

　 (2) 若拋物线的顶点为M，点P为线段OB上一动点(不与点

　　　 B重合)，点Q在线段MB上移动，且ÐMPQ=45°，设线

　　　 段OP=x，MQ=y₂，求y₂与x的函数关系式，并直接写出自变量x的取值范围；

　 (3) 在同一平面直角坐标系中，两条直线x=m，x=n分别与拋物线交于点E，G，与(2)中的

　　　 函数图像交于点F，H。问四边形EFHG能否为平行四边形？若能，求m，n之间的数量

　　　 关系；若不能，请说明理由。

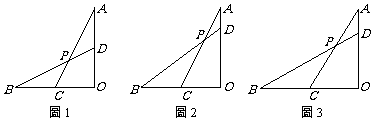
24. (本题满分10分) 已知：线段OA^OB，点C为OB中点，D为线段OA上一点。连结AC，

　 BD交于点P。

　 (1) 如图1，当OA=OB，且D为OA中点时，求的值；

　 (2) 如图2，当OA=OB，且=时，求tanÐBPC的值；

　 (3) 如图3，当AD：AO：OB=1：n：2时，直接写出tanÐBPC的值。

23. (本题满分10分) 某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间

　 会全部住满。当每个房间每天的房价每增加10元时，就会有一个房间空闲。宾馆需对游客

　 居住的每个房间每天支出20元的各种费用。根据规定，每个房间每天的房价不得高于340

　 元。设每个房间的房价每天增加x元(x为10的正整数倍)。

　 (1) 设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；

　 (2) 设宾馆一天的利润为w元，求w与x的函数关系式；

　 (3) 一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

22. (本题满分8分) 如图，点O在ÐAPB的平分在线，圆O与PA相切于

　 点C；

　 (1) 求证：直线PB与圆O相切；

　 (2) PO的延长线与圆O交于点E。若圆O的半径为3，PC=4。

　　　 求弦CE的长。

21. (本题满分7分) (1) 在平面直角坐标系中，将点A(-3，4)向右平移5个单位到点A₁，再将点

　 A₁绕坐标原点顺时针旋转90°到点A₂。直接写出点A₁，A₂的坐标；

　 (2) 在平面直角坐标系中，将第二象限内的点B(a，b)向右平移m个单位到第一象限点B₁，

　　　 再将点B₁绕坐标原点顺时针旋转90°到点B₂，直接写出点B₁，B₂的坐标；

　 (3) 在平面直角坐标系中。将点P(c，d)沿水平方向平移n个单位到点P₁，再将点P₁绕坐标

　　　 原点顺时针旋转90°到点P₂，直接写出点P₂的坐标。

20. (本题满分7分) 小伟和小欣玩一种抽卡片游戏：将背面完全相同，正面分别写有1，2，3，

　 4的四张卡片混合后，小伟从中随机抽取一张。记下数字后放回，混合后小欣再随机抽取一

　 张，记下数字。如果所记的两数字之和大于4，则小伟胜；如果所记的两数字之和不大于4，

　 则小欣胜。

　 (1) 请用列表或画树形图的方法。分别求出小伟，小欣获胜的概率；

　 (2) 若小伟抽取的卡片数字是1，问两人谁获胜的可能性大？为什么？