
6、在函数 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于 的点中,坐标为整数的点的个数是( )
的点中,坐标为整数的点的个数是( )
A.3 B.2 C.1 D.0
5、曲线 在点
在点 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A. B.
B. C.
C. D.
D.
3、设函数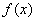 是
是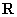 上以5为周期的可导偶函数,则曲线
上以5为周期的可导偶函数,则曲线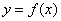 在
在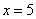 的切线的斜率为( )
的切线的斜率为( )
A.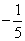 B.
B.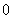 C.
C.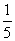 D.
D.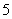
4设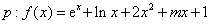 在
在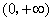 内单调递增,
内单调递增,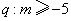 ,则
,则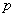 是
是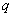 的
的
( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
2、设 则
则 ( )
( )
A sinx B –sinx C cosx D -cosx
1、函数f(x)= x3+ax+1在(-∞,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
x3+ax+1在(-∞,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
A B.1
C.
B.1
C. D.-1
D.-1
6.利用导数解决实际问题
例9用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
解:设长方体的宽为 (m),则长为
(m),则长为 (m),高为
(m),高为 .
.
故长方体的体积为
从而 令
令 ,解得
,解得 (舍去)或
(舍去)或 ,因此
,因此 .
.
当 时,
时, ;当
;当 时,
时, ,故在
,故在 处
处 取得极大值,并且这个极大值就是
取得极大值,并且这个极大值就是 的最大值,从而最大体积
的最大值,从而最大体积 ,此时长方体的长为2 m,高为1.5 m
,此时长方体的长为2 m,高为1.5 m
例10(2009年湖南高考)某地建一座桥,两端的桥墩已建好,这两墩相距 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。
万元。
(Ⅰ)试写出 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)当 =640米时,需新建多少个桥墩才能使
=640米时,需新建多少个桥墩才能使 最小?
最小?
解 (Ⅰ)设需要新建 个桥墩,
个桥墩,
所以 
= .
.
(Ⅱ) 由(Ⅰ)知 ,
,
令 ,得
,得 ,所以
,所以 =64
=64
当0< <64时
<64时 <0,
<0,  在区间(0,64)内为减函数;
在区间(0,64)内为减函数;
当 时,
时, >0.
>0.  在区间(64,640)内为增函数,
在区间(64,640)内为增函数,
所以 在
在 =64处取得最小值,此时,
=64处取得最小值,此时,
故需新建9个桥墩才能使 最小。
最小。
5. 利用导数求函数的极值与最值
例7(2009天津卷理)已知函数 其中
其中
(1) 当 时,求曲线
时,求曲线 处的切线的斜率;
处的切线的斜率;
(2) 当 时,求函数
时,求函数 的单调区间与极值。
的单调区间与极值。
(I)解:

(II)

以下分两种情况讨论。
(1) >
> ,则
,则 <
< .当
.当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
 |
 |
 |
 |
 |
 |
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |



(2) <
< ,则
,则 >
> ,当
,当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
 |
 |
 |
 |
 |
 |
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |



点评: 本小题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算能力及分类讨论的思想方法。
例8(2008年天津高考)已知函数 (
( ),其中
),其中 .若函数
.若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围.
的取值范围.
解: ,显然
,显然 不是方程
不是方程 的根.
的根.
为使 仅在
仅在 处有极值,必须
处有极值,必须 成立,即有
成立,即有 .
.
解不等式,得 .这时,
.这时, 是唯一极值.因此满足条件的
是唯一极值.因此满足条件的 的取值范围是
的取值范围是 .
.
3.利用导数解决函数的单调性问题
例5(2008全国高考)已知函数 ,
, .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)设函数 在区间
在区间 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.
解:(1) 求导得
求导得
当 时,
时, ,
, ,
, 在
在 上递增;
上递增;
当 ,
, 求得两根为
求得两根为 ,
,
即 在
在 递增,
递增, 递减,
递减,  递增。
递增。
(2)因为函数 在区间
在区间 内是减函数,所以当
内是减函数,所以当 时
时 恒成立,结合二次函数的图像可知
恒成立,结合二次函数的图像可知 解得
解得 .
.
点评:函数在某区间上单调转化为导函数 或
或 在区间上恒成立问题,是解决这类问题的通法.本题也可以由函数在
在区间上恒成立问题,是解决这类问题的通法.本题也可以由函数在 上递减,所以
上递减,所以 求解.
求解.
[变式1](2004年全国高考)若函数 在区间
在区间 上是减函数,在区间
上是减函数,在区间 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
解: ,令
,令 得
得 或
或 ,结合图像知
,结合图像知 ,故
,故 .
.
点评:本题也可转化为 恒成立且
恒成立且 恒成立来解.
恒成立来解.
[变式2](2005年湖南高考)已知函数 存在单调递减区间,求a的取值范围;
存在单调递减区间,求a的取值范围;
解: 因为函数
因为函数 存在单调递减区间,所以
存在单调递减区间,所以 在
在 上解,从而
上解,从而 有正解.
有正解.
①当 时,
时, 为开口向上的抛物线,
为开口向上的抛物线, 总有正解;
总有正解;
②当 时,
时, 为开口向下的抛物线,要使
为开口向下的抛物线,要使 总有正解,则
总有正解,则 ,解得
,解得 .
.
综上所述,a的取值范围为 .
.
[变式3](2009浙江高考)已知函数
 .若函数
.若函数 在区间
在区间 上不单调,求
上不单调,求 的取值范围.
的取值范围.
解:函数 在区间
在区间 不单调,等价于
不单调,等价于 在区间
在区间 上有实数解,且无重根.
上有实数解,且无重根.
又 ,由
,由 ,得
,得 。从而
。从而
 或
或 解得
解得 或
或
所以 的取值范围是
的取值范围是
点评:这种逆向设问方式是今后高考命题的一种趋势,充分体现高考“能力立意”的思想,高考中应高度重视。
(4)利用导数的几何意义研究曲线的切线问题
例6 (2009江西高考)若存在过点 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 等于
等于
A. 或
或 B.
B. 或
或 C.
C. 或
或 D.
D. 或
或
解:设过 的直线与
的直线与 相切于点
相切于点 ,所以切线方程为
,所以切线方程为
即 ,又
,又 在切线上,则
在切线上,则 或
或 ,
,
当 时,由
时,由 与
与 相切可得
相切可得 ,
,
当 时,由
时,由 与
与 相切可得
相切可得 ,所以选
,所以选 .
.
点评:函数的切线问题,切点是关键,因为它是联结曲线和其切线的“桥梁”,在做题中往往需要设出切点.
[变式](2008辽宁高考)设 为曲线
为曲线 :
: 上的点,且曲线
上的点,且曲线 在点
在点 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为 ,则点
,则点 横坐标的取值范围为( )
横坐标的取值范围为( )
A. B.
B. C.
C. D.
D.
解:由曲线 在点
在点 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为 ,可得曲线
,可得曲线 在点
在点 处切线的斜率范围为
处切线的斜率范围为 ,又
,又 ,设点
,设点 的横坐标为
的横坐标为 ,则
,则 ,解得
,解得 ,故选
,故选 .
.
2. 利用导数研究函数的图像
例3 (2009安徽高考)设 <b,函数
<b,函数 的图像可能是
的图像可能是
解: ,由
,由 得
得 ,∴当
,∴当 时,
时, 取极大值0,当
取极大值0,当 时
时 取极小值且极小值为负.故选C.或当
取极小值且极小值为负.故选C.或当 时
时 ,当
,当 时,
时, 选C.
选C.
点评:通过导数研究函数图像的变化规律,也是考试的热点题型.
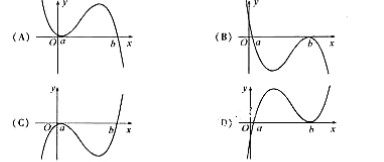
例4(2009年湖南卷)若函数 的导函数在区间
的导函数在区间 上是增函数,
上是增函数,
则函数 在区间
在区间 上的图象可能是
上的图象可能是
|

A . B. C. D.
解: 因为函数 的导函数
的导函数 在区间
在区间 上是增函数,即在区间
上是增函数,即在区间 上各点处函数的变化率是递增的,故图像应越来越陡峭.由图易知选A.
上各点处函数的变化率是递增的,故图像应越来越陡峭.由图易知选A.
点评:这是一道非常精彩的好题,题目考察了导数的概念--函数的变化率以及图像的变化规律,是以高等数学中函数图像的凹凸性为背景命制的,虽然试题的设计来源于高等数学,但考察的还是中学所学的初等数学知识.这也是近年来高考命题的一大特色.
1.导数定义的应用
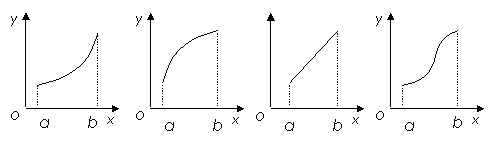
 例1 (2008北京高考)如图,函数
例1 (2008北京高考)如图,函数 的图象是折线段
的图象是折线段 ,其中
,其中 的坐标分别为
的坐标分别为 ,
,  _________.
_________.
解:由图可知 ,根据导数的定义
,根据导数的定义
知
 .
.
例2(2006重庆高考)已知函数 ,其中
,其中 ,(Ⅰ)略,(Ⅱ)若
,(Ⅰ)略,(Ⅱ)若 且
且 ,试证:
,试证: .
.
解: ,易知
,易知 .故
.故
 ,
,
所以 解得
解得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com