
22.解:(1)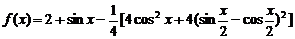
=2+sinx-cos2x-1+sinx=sin2x+2sinx
(1) 设函数y=f (x)的图象上任一点M(x0,y0)关于原点的对称点为N(x,y)
则x0= -x,y0= -y
∵点M在函数y=f (x)的图象上
 ,即y= -sin2x+2sinx
,即y= -sin2x+2sinx
∴函数g(x)的解析式为g(x)= -sin2x+2sinx
(3)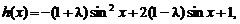 设sinx=t,(-1≤t≤1)
设sinx=t,(-1≤t≤1)
则有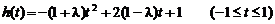
① 当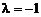 时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
时,h(t)=4t+1在[-1,1]上是增函数,∴λ= -1
② 当 时,对称轴方程为直线
时,对称轴方程为直线 .
.
ⅰ) 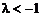 时,
时,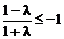 ,解得
,解得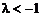
ⅱ)当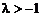 时,
时,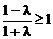 ,解得
,解得
综上, .
.
已知向量 满足
满足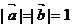 ,且
,且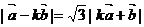 ,其中
,其中 。
。
(1)试用k表示 ,并求出
,并求出 的最大值及此时
的最大值及此时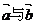 的夹角
的夹角 的值。
的值。
(2)当 取得最大值时,求实数
取得最大值时,求实数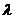 ,使
,使 的值最小,并对这一结果作出几何解释
的值最小,并对这一结果作出几何解释
(1)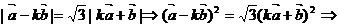

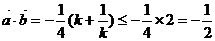 ,此时
,此时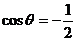
即 的最大值为
的最大值为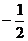 ,此时
,此时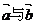 的夹角
的夹角 的值为
的值为 。
(6分)
。
(6分)
(2)由题意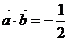 ,故
,故
∴ 当
当 时,
时, 的值最小,此时
的值最小,此时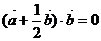
即当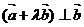 时,
时, 的值最小。
的值最小。
如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、
(5,2)、(-3,0),点N在AC上,且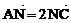 ,AM与BN的交点为P,求:
,AM与BN的交点为P,求:
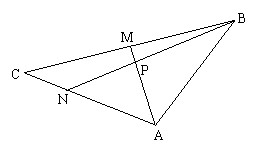 (1)点P分向量
(1)点P分向量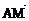 所成的比
所成的比 的值;
的值;
(2)P点坐标.
解:(1)∵A、B、C三点坐标分别为 、
、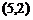 、
、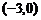
由于M为BC中点,可得M点的坐标为(1,1) ………1分
由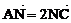 可得N点的坐标为
可得N点的坐标为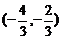 ……1分
……1分
又由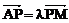 可得P点的坐标为(
可得P点的坐标为(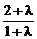 ,
,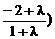 …1分
…1分
从而得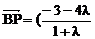 ,
,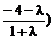
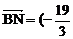 ,
, ……………2分
……………2分
∵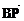 与
与 共线 故有
共线 故有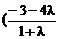 )
)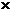
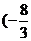 )-(
)-(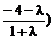
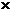 (
( =0 …2分
=0 …2分
解之得 4
……………2分
4
……………2分
∴点P的坐标为(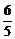 ,
, )
)
正六边形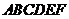 的中心为点
的中心为点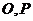 为平面
为平面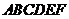 上异于
上异于 的任意一点, 且
的任意一点, 且
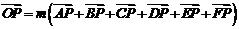 ,则实数
,则实数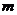 的值为C
的值为C
A、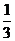 B、
B、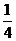 C、
C、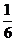 D、不确定
D、不确定
已知 的面积
的面积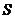 满足
满足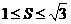 ,且
,且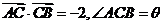
(1)求函数 的最大值;
的最大值;
(2)若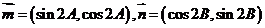 ,求
,求 的取值范围。
的取值范围。
解:(1)如图:由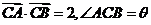
得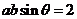 ,
,
∵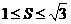 ∴
∴ 而
而
∴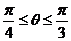 ………………………………………… 2分
………………………………………… 2分
∵ 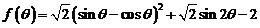
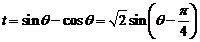
∵ ∴
∴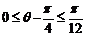 从而
从而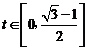
∴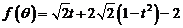
 …………………………… 5分
…………………………… 5分
∵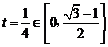
∴当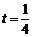 时,
时, 有最大值
有最大值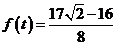 ………………… 7分
………………… 7分
(2)∵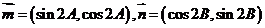 …………………… 9分
…………………… 9分
∴

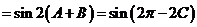
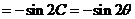 ………………………………… 10分
………………………………… 10分
∴
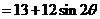 ………………………………… 11分
………………………………… 11分
∵ ∴
∴
∴
故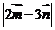 的取值范围为
的取值范围为 ………………………………… 13分
………………………………… 13分
已知 的面积
的面积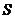 满足
满足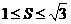 ,且
,且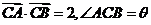
(1)求函数 的值域;
的值域;
(2)若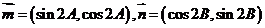 ,求
,求 的最大值。
的最大值。
11. 解析:
解析:
O为△ABC所在平面内一点, 且满足 =0,则△ABC的形状为( A
)
=0,则△ABC的形状为( A
)
A. 等腰△ B. 直角△ C.等腰Rt△ D.等边△
将向量 绕原点O逆时针旋转450,得向量
绕原点O逆时针旋转450,得向量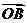 ,则
,则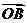 的坐标为(C )
的坐标为(C )
A. 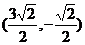 B.
B. 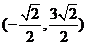 C.
C.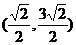 D.
D.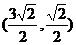
已知向量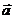 、
、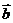 、
、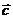 、
、 及实数x、y满足
及实数x、y满足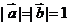 ,
, ,
, ,若
,若 ,
, 且
且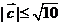 .
.
(1) 求y关于x的函数关系式y = f(x)及其定义域;
(2) 若x Î [1,2]时,不等式f(x) ³ mx - 16恒成立,求实数m的取值范围.
解:(1) ∵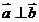 ,∴
,∴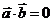 ,
,
又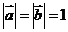 ,∴
,∴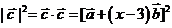 = 1 + (x - 3)2,
= 1 + (x - 3)2,
∵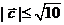 ,∴1 + (x - 3)2
£ 10,解得0 £ x
£ 6,
,∴1 + (x - 3)2
£ 10,解得0 £ x
£ 6,
又∵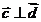 ,∴
,∴ ,而
,而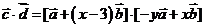 = - y + x(x
- 3),
= - y + x(x
- 3),
∴- y + x(x - 3) = 0,∴y = f(x) = x(x - 3),其定义域为[0,6].
(2) 当1 £ x £ 2时,欲使f(x) ³ mx - 16恒成立,
即使x2 - 3x
³ mx - 16恒成立,亦即m £ x
+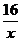 - 3恒成立,
- 3恒成立,
令g(x) = x +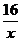 ,当1 £ x
£ 2时,[g(x)]min = 10,∴m
£ 7.
,当1 £ x
£ 2时,[g(x)]min = 10,∴m
£ 7.
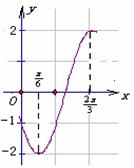
函数 (A> 0, w>0)的部分图象如右所示, 则它的解析式是 __ y= 2sin(2x –
(A> 0, w>0)的部分图象如右所示, 则它的解析式是 __ y= 2sin(2x –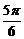 ) ________ .
) ________ . 
设向量 ,若
,若 (tÎR),则
(tÎR),则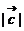 的最小值为( C )
的最小值为( C )
A.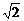 B.1
C.
B.1
C. D.
D.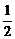
已知
(Ⅰ)若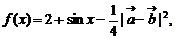 求
求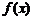 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若 在
在 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
2.
(2) 解:∵me1+e2与e1-e2垂直
∴(m e1+e2)·(e1-e2)= ,即me
,即me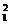 +(1-m)e1·e2-e
+(1-m)e1·e2-e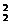 =0 8分
∵|e1|=2,|e2|=3,e1与e2的夹角为60°
∴e
=0 8分
∵|e1|=2,|e2|=3,e1与e2的夹角为60°
∴e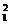 =| e1|2=4,e
=| e1|2=4,e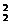 =| e2|2=9,e1·e2=| e1|·| e2|cos
=| e2|2=9,e1·e2=| e1|·| e2|cos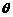 =2×3×cos60°=3 10分
∴4m+3(1-3m)-9=0,m=6.
已知向量a=(cos2x,sin2x),b=(cos x,sin x) (x ÎR), 设f (x)=3 | a+b |+m | a-b | (m为正常数).
(1)求a·b;
(2)当m=3时,求证:f (x+p )=f (x )对一切实数x恒成立;
(3)当m≠3时,函数f (x)的最小值是否能等于1,若能,请求出m的值,若不能,请说明理由.
=2×3×cos60°=3 10分
∴4m+3(1-3m)-9=0,m=6.
已知向量a=(cos2x,sin2x),b=(cos x,sin x) (x ÎR), 设f (x)=3 | a+b |+m | a-b | (m为正常数).
(1)求a·b;
(2)当m=3时,求证:f (x+p )=f (x )对一切实数x恒成立;
(3)当m≠3时,函数f (x)的最小值是否能等于1,若能,请求出m的值,若不能,请说明理由.
解:(1) a·b=cos2xcos x+sin2xsin x=cos x 2分
(2) ∵| a+b |2=| a | 2+2 a·b+| b |2=2+2cos x= ,∴| a+b | =2| cos
,∴| a+b | =2| cos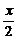 |
同理:| a-b|=2| sin
|
同理:| a-b|=2| sin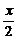 | 4分
∴当m=3时,f (x)=3| a+b |+3| a-b |=6| cos
| 4分
∴当m=3时,f (x)=3| a+b |+3| a-b |=6| cos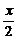 |+6| sin
|+6| sin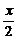 |
∴
|
∴ 即有
即有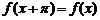 6分
6分
(3) 当m≠3时,f (x)=3| a+b|+m | a-b |=6| cos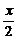 |+2m| sin
|+2m| sin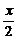 |
∵
|
∵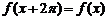 ,∴f (x) 的周期是
,∴f (x) 的周期是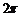 ,故可设0≤x≤
,故可设0≤x≤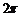 8分
①当0≤x≤
8分
①当0≤x≤ 时,0≤
时,0≤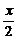 ≤
≤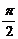 ,
∴
,
∴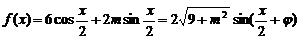 其中
其中 ,
, ,且j Î(0,
,且j Î(0,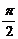 ) 10分
∵
) 10分
∵  ,∴f (x)的最小值为:
,∴f (x)的最小值为:
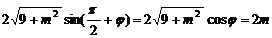 由2m = 1得
由2m = 1得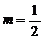 12分
② 当p≤x≤2p 时,
12分
② 当p≤x≤2p 时, 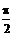 £
£ 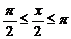 ∴
∴ 其中
其中 ,
, ,且j Î(0,
,且j Î(0,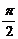 )
∵
)
∵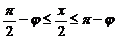 ,同理可得:
,同理可得: 综上,存在
综上,存在 ,使f (x )的最小值为1.
,使f (x )的最小值为1.
在锐角 中,
中,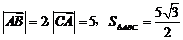 ,那么
,那么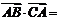 (B )
(B )
A、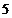 B、
B、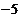 C、
C、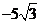 D、
D、
如图,O是△ABC内的一点,∠AOB=150°,∠AOC=120°,向量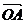 、
、 、
、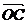 的模分别为2、1、3.
的模分别为2、1、3.
(1)求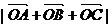 ;
;
(2)若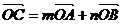 ,求实数m、n的值.
,求实数m、n的值.
(1)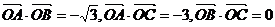
∴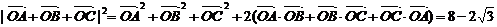
∴
(2)方法1:设 =m
=m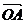 ,
,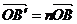 .由向量加法及数乘向量的几何意义m<0, n<0,且∠COB′=90°,∠CB′D=30°
.由向量加法及数乘向量的几何意义m<0, n<0,且∠COB′=90°,∠CB′D=30°
∴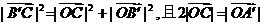
∴4m2=n2+9,且6=2|m|, ∴m=-3,n=-3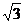
方法2:以O为原点,OA为x轴建立直角坐标系,
则:A(2,0),B(cos150°, sin150°), C(3cos240°, 3sin240°),
即A(2,0),B( ,
,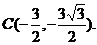
由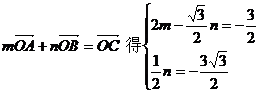 即
即
已知向量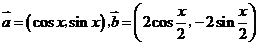 ,且
,且 ,
,
求:(1)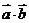 和
和 的取值范围;
的取值范围;
(2)函数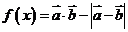 的最小值。
的最小值。
解:(1)∵
∴
又∵ ∴
∴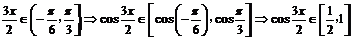
∴ 即
即
∵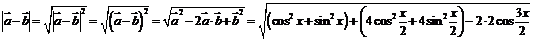
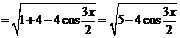
又∵ ∴
∴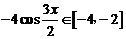 ∴
∴
(2)由(1)知: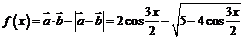
设 ,则
,则 ,
,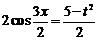
∴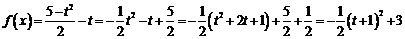
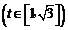
∴由图象可知:当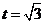 时,函数
时,函数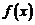 取得最小值
取得最小值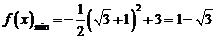
函数 的一条对称轴方程是 ( A )
的一条对称轴方程是 ( A )
A.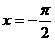 B.
B.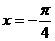 C.
C.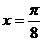 D.
D.
如图,某观测站C在城A的南偏西 方向上,从城A出发有一条公路,走向是南偏东
方向上,从城A出发有一条公路,走向是南偏东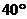 ,在C处测得距离C处31千米的公路上的B处有一辆正沿着公路向城A驶去,行驶了20千米后到达D处,测得C、D二处间距离为21千米,这时此车距城A多少千米?
,在C处测得距离C处31千米的公路上的B处有一辆正沿着公路向城A驶去,行驶了20千米后到达D处,测得C、D二处间距离为21千米,这时此车距城A多少千米?
已知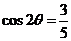 ,则
,则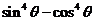 的值为
的值为
1. 给出下列三组向量:
①e1=(-1,2),e2=(5,7); ②e1=(3,5),e2=(6,10); ③e1=(2,-3),e2=(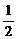 ,
,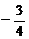 ).
其中有一组能作为表示它们所在平面内所有向量的基底,正确的判断是A
A.① B.①③ C.②③ D.①②③
).
其中有一组能作为表示它们所在平面内所有向量的基底,正确的判断是A
A.① B.①③ C.②③ D.①②③
设两个非零向量e1和e2不共线.
(1)如果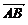 =e1+e2,
=e1+e2,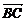 =2e1+8e2,
=2e1+8e2, =3e1-3e2,求证:A、B、D三点共线;
(2)若| e1 |=2,| e2 |=3,e1与e2的夹角为60°,me1+e2与e1-e2垂直,求实数m的值.
(1)证明:∵
=3e1-3e2,求证:A、B、D三点共线;
(2)若| e1 |=2,| e2 |=3,e1与e2的夹角为60°,me1+e2与e1-e2垂直,求实数m的值.
(1)证明:∵ (2e1+8e2)+(3e1-3e2)=5 e1+5e2=5
(2e1+8e2)+(3e1-3e2)=5 e1+5e2=5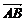 2分
∴
2分
∴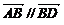 ,又
,又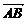 与
与 有共同点B 4分
∴ A、B、D三点共线 6分
有共同点B 4分
∴ A、B、D三点共线 6分
16.解析:(1)由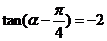 知,
知, ,即
,即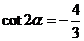
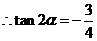 ,又
,又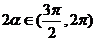 ,可得
,可得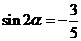
(2)由 知,
知,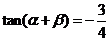
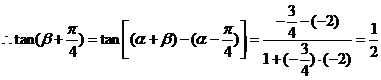
12.在 中,已知
中,已知 ,b,c是角A、B、C的对应边,则①若
,b,c是角A、B、C的对应边,则①若 ,则
,则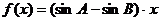 在R上是增函数;②若
在R上是增函数;②若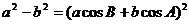 ,则
,则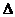 ABC是
ABC是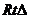 ;③
;③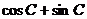 的最小值为
的最小值为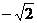 ;④若
;④若 ,则A=B;⑤若
,则A=B;⑤若 ,则
,则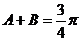 ,其中错误命题的序号是_____。
,其中错误命题的序号是_____。
正解:错误命题③⑤。
① 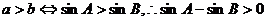
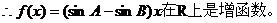
② 。
。
③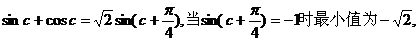
显然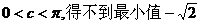 。
。
④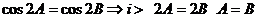
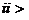
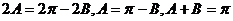 (舍) ,
(舍) , 。
。
⑤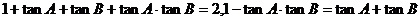

 错误命题是③⑤。
错误命题是③⑤。
在 中,
中,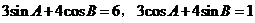 ,则
,则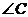 的大小为( )
的大小为( )
A. 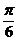 B.
B.
 C.
C.
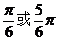 D.
D.
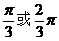
解析:由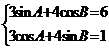 平方相加得
平方相加得 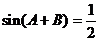

若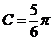 则
则
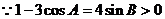

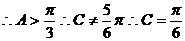
 选A
选A
点评:此题极易错选为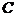 ,条件
,条件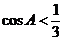 比较隐蔽,不易发现。探索
比较隐蔽,不易发现。探索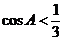 ,可以充分利用
,可以充分利用 ,从已知条件中尝试。但是可能一次找不准,比如
,从已知条件中尝试。但是可能一次找不准,比如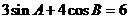 ,
,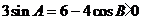 ,恒成立。
,恒成立。
△ABC中,已知cosA=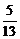 ,sinB=
,sinB= ,则cosC的值为( )
,则cosC的值为( )
A、 B、
B、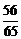 C、
C、 或
或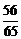 D、
D、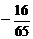
答案:A
点评:易误选C。忽略对题中隐含条件的挖掘
已知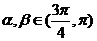 ,
,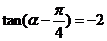 ,
,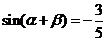 .
.
(1)求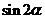 的值;
的值;
(2)求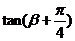 的值.
的值.
14.火车、飞机、赛车正式启动或制动过程中的运动通常是变速直线运动.人们设法测得了它们在启动或制动过程中各个不同时刻的速度,如下列各表所示:
表1:火车在启动过程中各时刻的速度(火车启动时开始计时)
|
时间(s) |
0 |
5 |
10 |
15 |
20 |
25 |
|
速度(m/s) |
0 |
1 |
2 |
3 |
4 |
5 |
表2:飞机在启动过程中各时刻的速度(从飞机启动一段时间后开始计时)
|
时间(s) |
0 |
5 |
10 |
15 |
20 |
25 |
|
速度(m/s) |
10 |
25 |
40 |
55 |
70 |
85 |
表 3:赛车在制动过程中各时刻的速度(赛车制动时开始计时)
|
时间(s) |
0 |
5 |
10 |
15 |
20 |
25 |
|
速度(m/s) |
25 |
20 |
15 |
10 |
5 |
0 |
请你认真分析和比较上述表格所提供的有关数据,并完成下列要求:
火车在启动过程中的速度随时间变化的特点(定量关系)可初步归纳为 ;飞机在启动过程中的速度随时间变化的特点(定量关系)可初步归纳为 ;赛车在制动过程中的速度随时间变化的特点(定量关系)可初步归纳为 .

13.某高速公路规定小汽车行驶速度不得超过120km/h.执勤的交通警察截住了一辆正在超速行驶的小汽车,“您的车速超过了120 km每小时的限制……”内勤交警对司机敬礼道.还没等司机回答,一名车内的小朋友抢着答道:“我们只开了几分钟,既不够1h,更不到120km……”假如你当时在场,应该怎样向这位小朋友解释呢?
12.(太原市中考题)下表是卡车沿直线平稳行驶和电车、机车起动过程中各个不同时刻的速度(从起动一段时间后开始计时),请你比较和分析表中的数据.

回答下列问题:
(1)卡车做 运动;
(2)电车的速度与时间的关系(定性)是 ;
(3)电车的速度v与时间t的定量关系式是v= ;
(4)通过分析电车和机车的速度随时间变化的规律,发现他们 是相同的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com