
5、下列对ATP的叙述中,错误的是( C )
A.ATP可以水解为一个核苷酸分子和两个磷酸分子
B.它的分子中含有两个高能磷酸键
C.细胞质中有ATP的分布,细胞核中无ATP的分布
D.正常细胞中的ATP与ADP的比值在一定范围内变化,并处于动态平衡之中
 [解析]ATP是生物体各项生命活动的直接能源物质,分布在需要能量的部位。在细胞核中进行DNA的复制、转录等均需要能量,故细胞核中有ATP的分布。
[解析]ATP是生物体各项生命活动的直接能源物质,分布在需要能量的部位。在细胞核中进行DNA的复制、转录等均需要能量,故细胞核中有ATP的分布。
4、德国科学家西诺西和吕克·蒙塔尼因发现遗传物质是RNA的艾滋病病毒(HIV)而获得2008年诺贝尔生理学或医学奖。下列关于生物体内的RNA叙述错误的是( C )
A. 生物的遗传物质只能是DNA或者是RNA
B. RNA具有多种生理功能,如遗传功能、催化功能等
C. HIV是通过自身RNA的自我复制在体外完成增殖
D. RNA分子中含有核糖,DNA分子中含有脱氧核糖
[解析]所有病毒都不能在体外完成增殖,只有寄生在宿主细胞内才能完成增殖,且HIV是逆转录病毒。
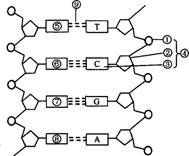
3.赫尔希和蔡斯分别用35S和32P标记T2噬菌体的蛋白质和DNA组分,下列被标记的部位组合正确的是( D )
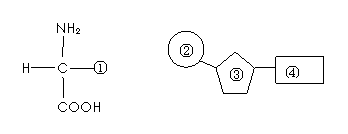
A.②① B.①③ C.④① D.①②
[解析]从图中可以判断出:①是氨基酸的R基,R基上可含有S元素,如半胱氨酸;②是磷酸基团,是DNA中含有磷酸的部位。噬菌体侵染细菌的实验中,应该用35S标记T2噬菌体的蛋白质,用32P标记T2噬菌体的DNA。
2.原核生物细胞和真核生物细胞中都存在的结构或物质是( B )
①核膜 ②核糖体 ③高尔基体 ④ATP合成酶
⑤细胞膜 ⑥RNA聚合酶 ⑦DNA解旋酶
A.①②④⑤⑦ B.②④⑤⑥⑦ C.②③④⑤⑦ D.②③④⑥⑦
[解析]原核生物细胞没有成形的细胞核,只有核糖体一种细胞器,所以不能选①③。
1. 下图表示真核生物细胞部分结构的功能,下列与此相关的叙述,错误的是( B )
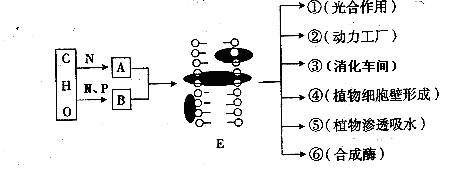
A.图中物质A表示蛋白质,物质B表示磷脂
B.E的结构特点是具有一定的选择透过性
C.抗体的分泌体现了E的流动性
D.完成③、④、⑤功能的结构均具有单层膜结构
[解析]图中E表示生物膜,生物膜的结构特点是具有一定的流动性,故B错误。
21.(本小题满分13分)
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中点, P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
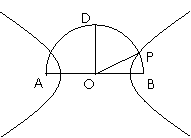 (Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅱ)设过点D的直线l与双曲线C相交于不同两点E、F,
若△OEF的面积不小于2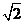 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
[解](Ⅰ)方法一:以O为原点,AB、OD所在直线分别
为x轴、y轴建立平面直角坐标系,则
点A(-2,0),B(2,0),P(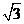 ,1).
(2分)
,1).
(2分)
设双曲线实半轴长为a,虚半轴长为b,半焦距为c,则
2a=|PA|-|PB|=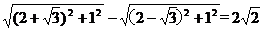 ,2c=|AB|=4. (3分)
,2c=|AB|=4. (3分)
所以a=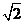 ,c=2,从而b2=c2-a2=2.
(4分)
,c=2,从而b2=c2-a2=2.
(4分)
故双曲线C的方程是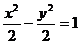 .
(5分)
.
(5分)
方法二:以O为原点,AB、OD所在直线分别为x轴、y轴建立平面直角坐标系,则
点A(-2,0),B(2,0),P(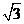 ,1).
(2分)
,1).
(2分)
设双曲线C的方程为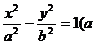 >0,b>0),则
>0,b>0),则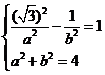 .
(3分)
.
(3分)
解得a2=b2=2,故双曲线C的方程是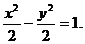 (5分)
(5分)
(Ⅱ)据题意可设直线l的方程为y=kx+2,代入双曲线C的方程得,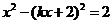 ,即
,即
(1-k2)x2-4kx-6=0. (6分)
因为直线l与双曲线C相交于不同两点E、F,则
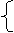
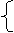
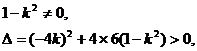 即
即 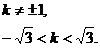 (7分)
(7分)
设点E(x1,y1),F(x2,y2),则x1+x2=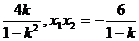 .
(8分)
.
(8分)
所以|EF|=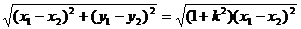
=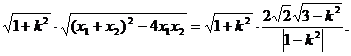 (9分)
(9分)
又原点O到直线l的距离d=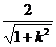 .
(10分)
.
(10分)
所以S△DEF=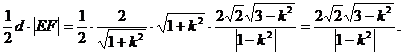 (11分)因为S△OEF
(11分)因为S△OEF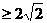 ,则
,则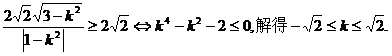 (12分)
(12分)
综上分析,直线l的斜率的取值范围是[-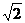 ,-1)
,-1)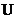 (-1,1)
(-1,1)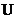 (1,
(1,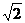 ]. (13分)
]. (13分)
20.(本小题满分13分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元-1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;
(Ⅱ)现有两个奖励函数模型:(1)y=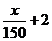 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
[解](Ⅰ)设奖励函数模型为y=f(x),则公司对函数模型的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③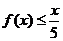 恒成立. (3分)
恒成立. (3分)
(Ⅱ)(1)对于函数模型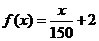 :
:
当x∈[10,1000]时,f(x)是增函数,则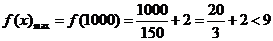 .
.
所以f(x)≤9恒成立. (5分)
因为函数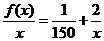 在[10,1000]上是减函数,所以
在[10,1000]上是减函数,所以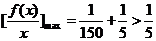 .
.
从而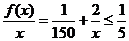 ,即
,即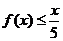 不恒成立.
不恒成立.
故该函数模型不符合公司要求. (8分)
(2)对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数,则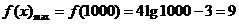 .
.
所以f(x)≤9恒成立. (10分)
设g(x)=4lgx-3-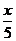 ,则
,则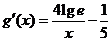 .
.
当x≥10时,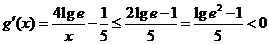 ,所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.所以4lgx-3-
,所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.所以4lgx-3-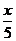 <0,即4lgx-3<
<0,即4lgx-3<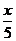 ,所以
,所以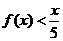 恒成立.
恒成立.
故该函数模型符合公司要求. (13分)
19.(本小题满分13分)
设数列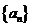 的前
的前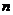 项和为
项和为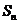 ,如果
,如果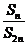 为常数,则称数列
为常数,则称数列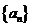 为“科比数列”.
为“科比数列”.
(Ⅰ)已知等差数列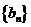 的首项为1,公差不为零,若
的首项为1,公差不为零,若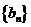 为“科比数列”,求
为“科比数列”,求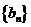 的通项公式;
的通项公式;
(Ⅱ)设数列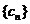 的各项都是正数,前
的各项都是正数,前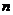 项和为
项和为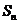 ,若
,若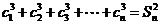 对任意
对任意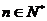 都成立,试推断数列
都成立,试推断数列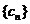 是否为“科比数列”?并说明理由.
是否为“科比数列”?并说明理由.
[解](Ⅰ)设等差数列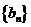 的公差为
的公差为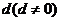 ,
,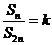 ,因为
,因为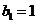 ,则
,则
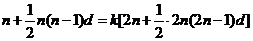 ,即
,即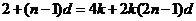 . (2分)
. (2分)
整理得,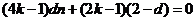 .
(3分)
.
(3分)
因为对任意正整数 上式恒成立,则
上式恒成立,则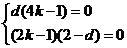 ,解得
,解得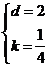 .
(5分)
.
(5分)
故数列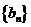 的通项公式是
的通项公式是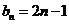 .
(6分)
.
(6分)
(Ⅱ)由已知,当 时,
时,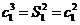 .因为
.因为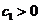 ,所以
,所以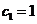 .
(7分)
.
(7分)
当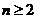 时,
时,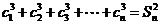 ,
,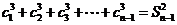 .
.
两式相减,得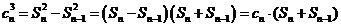 .
.
因为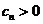 ,所以
,所以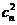 =
=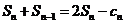 .
(9分)
.
(9分)
显然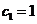 适合上式,所以当
适合上式,所以当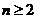 时,
时,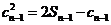 .
.
于是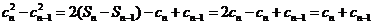 .
.
因为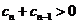 ,则
,则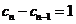 ,所以数列
,所以数列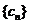 是首项为1,公差为1的等差数列.(12分)
是首项为1,公差为1的等差数列.(12分)
所以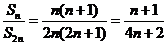 不为常数,故数列
不为常数,故数列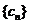 不是“科比数列”.
(13分)
不是“科比数列”.
(13分)
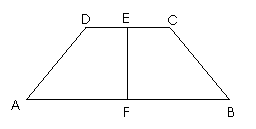
18.(本小题满分12分)
在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC=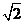 .沿EF将梯形AFED折起,使得∠AFB=60°,如图.
.沿EF将梯形AFED折起,使得∠AFB=60°,如图.
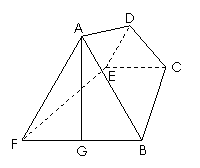 (Ⅰ)若G为FB的中点,求证:AG⊥平面BCEF;
(Ⅰ)若G为FB的中点,求证:AG⊥平面BCEF;
 (Ⅱ)求二面角C-AB-F的正切值.
(Ⅱ)求二面角C-AB-F的正切值.
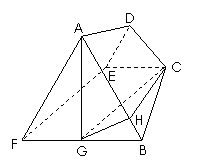 [解](Ⅰ)因为AF=BF,∠AFB=60°,△AFB为等边三角形.
[解](Ⅰ)因为AF=BF,∠AFB=60°,△AFB为等边三角形.
又G为FB的中点,所以AG⊥FB. (2分)
在等腰梯形ABCD中,因为E、F分别是CD、AB的中点,
所以EF⊥AB.于是EF⊥AF,EF⊥BF,则EF⊥平面ABF,
所以AG⊥EF. (4分)
又EF与FB交于一点F,所以AG⊥平面BCEF. (5分)
(Ⅱ)解法一:连接CG,因为在等腰梯形ABCD中,
CD=2,AB=4,E、F分别是CD、AB中点,
所以EC=FG=BG=1,从而CG∥EF.
因为EF⊥面ABF,所以CG⊥面ABF. (7分)
过点G作GH⊥AB于H,连结CH,据三垂线定理有CH⊥AB,所以∠CHG为二面角C-AB-F的平面角. (9分)
因为Rt△BHG中,BG=1,∠GBH=60°,所以GH=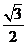 .
(10分)
.
(10分)
在Rt△CGB中,CG⊥BG,BG=1,BC=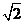 ,所以CG=1.
(11分)
,所以CG=1.
(11分)
在Rt△CGH中,tan∠CHG=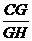 =
=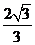 ,故二面角C-AB-F的正切值为
,故二面角C-AB-F的正切值为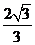 . (12分)
. (12分)
解法二:如图所示建立空间直角坐标系,由已知可得,
 点B(2,0,0),A(1,0,
点B(2,0,0),A(1,0,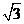 ),C(1,1,0).
(7分)
),C(1,1,0).
(7分)
因为EF⊥平面ABF,所以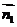 =(0,1,0)为
=(0,1,0)为
平面ABF的一个法向量. (8分)
设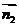 =(x,y,z)为平面ABCD的法向量,
=(x,y,z)为平面ABCD的法向量,
因为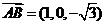 ,
,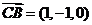 ,
,
由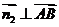 ,
,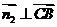 ,得
,得
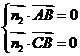 , 即
, 即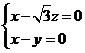 .
.
令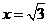 ,则
,则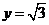 ,z=1,所以
,z=1,所以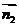 =(
=( ,
,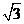 ,1). (10分)
,1). (10分)
所以cos<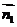 ,
,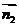 >=
>=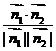 =
=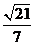 .
(11分)
.
(11分)
从而tan<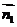 ,
,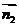 >=
>=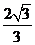 ,故二面角C-AB-F的正切值为
,故二面角C-AB-F的正切值为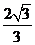 .
(12分)
.
(12分)
17.(本小题满分12分)
为了参加师大附中第23届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根a元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求a的值.
[解](Ⅰ)因为6根竹竿的长度从小到大依次为3.6,3.8,4.0,4.1,4.3,4.5,其中长度之差超过0.5米的两根竹竿长可能是3.6和4.3,3.6和4.5,3.8和4.5. (3分)
设“抽取两根竹竿的长度之差不超过0.5米”为事件A,则
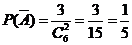 ,所以
,所以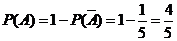 .
.
故所求的概率为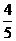 .
(6分)
.
(6分)
(Ⅱ)设任取两根竹竿的价格之和为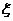 ,则
,则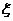 的可能取值为
的可能取值为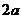 ,
, ,20.
(7分)
,20.
(7分)
其中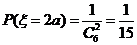 ,
,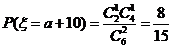 ,
,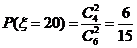 . (10分)
. (10分)
所以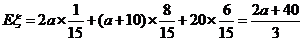 .
(11分)
.
(11分)
令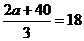 ,得a=7. (12分)
,得a=7. (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com