5、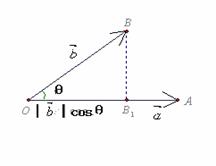研究数量积的几何意义

(1)给出向量投影的概念：

如图，我们把││cosθ(││cosθ)

叫做向量在方向上(在方向上)的投影，

记做：OB₁=││cosθ

(2)提出问题5：数量积的几何意义是什么？

答：数量积·等于的长度︱︱与在的方向上的投影︱︱cosθ的乘积。

［设计意图］：这里将数量积的几何意义提前，使学生从代数和几何两个方面对数量积的特征有了更加充分的认识

4、学生讨论，并完成下表：

θ的范围	0°≤θ<90°	θ=90°	90°<θ≤180°
·的符号

［设计意图］：引导学生通过自主研究，明确两个向量的夹角决定它们的数量积的符号，进一步从细节上理解向量数量积的定义。

3、提出问题4：向量的数量积运算与线性运算的结果有什么不同？影响数量积大小的因素有哪些？

　 答：线性运算的结果是向量，而数量积的结果则是数量，这个数量的大小不仅和向量与的模有关，还和它们的夹角有关。

2、明晰数量积的定义

(1)　　 数量积的定义：

已知两个非零向量与，它们的夹角为θ，我们把数量︱︱·︱︱cosθ叫做与的数量积(或内积)，记作：·，即：·= ︱︱·︱︱cosθ

(2)定义说明：

①记法“·”中间的“·”不可以省略，也不可以用“ ”代替。　　

② “规定”：零向量与任何向量的数量积为零。

［设计意图］：1.认识向量的数量积的实际背景。2.使学生在形式上认识数量积的定义。3.从数学和物理两个角度创设问题情景，使学生明白为什么研究这种运算,从而产生强烈的求知欲望

1、给出有关材料并提出问题3：

(1)如图所示，一物体在力F的作用下产生位移S，

那么力F所做的功：W= |F| |S| cos。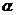

(2)这个公式有什么特点？请完成下列填空：

①W(功)是　　 量，②F(力)是　　 量，

③S(位移)是　 量，④α是　　　　　　 。

(3)你能用文字语言表述“功的计算公式”吗?

答：功是力与位移的大小及其夹角余弦的乘积

(4)如果我们将公式中的力与位移推广到一般向量，其结果又该如何表述？

答：两个向量的大小及其夹角余弦的乘积。

3、新课引入：本节课我们仍然按照这种研究思路来研究向量的另外一种运算。导入课题：平面向量数量积的物理背景及其含义

［设计意图］：1.明白新旧知识的联系性。2.明确研究向量的数量积这种运算的途径。

活动二：探究数量积的概念

2、提出问题2：请同学们继续回忆，我们是怎么引入向量的加法运算的？我们又是按照怎样的顺序研究了这种运算的？

答：物理模型→概念→性质→运算律→应用

活动一：创设问题情景，引出新课

1、提出问题1：请同学们回顾一下，我们已经研究了向量的哪些运算？这些运算的结果是什么？

答：向量的加法、减法及数乘运算。这些运算的结果是向量。　

重点是平面向量数量积的概念、用平面向量数量积表示向量的模及夹角；难点是平面向量数量积的定义及运算律的理解，平面向量数量积的应用。

3、体会类比的数学思想和方法，进一步培养学生抽象概括、推理论证的能力。