
1.含有三个实数的集合可以表示为 ,也可以表示为
,也可以表示为 ,则
,则 的值为
的值为
A. -1 B.0 C.1 D.-1或1
(二)
15.(本小题满分12分)
已知10件产品中有2件是次品.
(1)任意取出4件产品作检验,求其中恰有1件是次品的概率.
(2)为了保证使2件次品全部检验出的概率超过0.6,至少应抽取几件产品作检验?
16.(本小题满分12分)
已知 中,三内角
中,三内角 满足
满足 ,求
,求 的值.
的值.
17.(本小题满分14分)
如图,矩形 与
与 所在平面垂直,将矩形
所在平面垂直,将矩形 沿
沿 对折,使得翻折后点
对折,使得翻折后点 落在
落在 上,设
上,设 ,
, ,
, .
.


(1)试求 关于
关于 的函数解析式;
的函数解析式;
(2)当 取最小值时,指出点
取最小值时,指出点 的位置,并求出此时
的位置,并求出此时 与平面
与平面 所成的角;
所成的角;
(3)在条件(2)下,求三棱锥P-ADQ内切球的半径。
18.(本小题满分14分)
等比数列 的首项为
的首项为 ,公比
,公比 .
.
(1) 设 表示该数列的前
表示该数列的前 项的积,求
项的积,求 的表达式;
的表达式;
(2) 当 取何值时,
取何值时, 有最大值.
有最大值.
19.(本小题满分为14分)
已知函数 的图象过原点,且关于点
的图象过原点,且关于点 成中心对称.
成中心对称.
(1) 求函数 的解析式;
的解析式;
(2) 若数列 满足:
满足: ,求
,求 ,
, ,
, 的值,猜想数列
的值,猜想数列 的通项公式
的通项公式 ,并证明你的结论;
,并证明你的结论;
(3) 若数列 的前
的前 项和为
项和为 ,判断
,判断 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
20.(本小题满分14分)
已知函数 ,满足条件:
,满足条件:
① ;②
;②  ;③
;③  ;④当
;④当 时,有
时,有 .
.
(1) 求 ,
, 的值;
的值;
(2) 由 ,
, ,
, 的值,猜想
的值,猜想 的解析式;
的解析式;
(3) 证明你猜想的 的解析式的正确性.
的解析式的正确性.
14、▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
①若 ,则
,则 的最小值是
;
的最小值是
;
② 极坐标方程 所表示的曲线是 ;
所表示的曲线是 ;
③在 中,
中,
 于点
于点 ,
, ,则
,则 = ;
= ;
13. 某气象站天气预报准确率是80%,5次预报中至少有4次准确的概率是______(精确到0.01);
12.已知函数 的图象经过点(2,1),则函数
的图象经过点(2,1),则函数
 的值域为 ;
的值域为 ;
11.若关于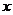 的方程
的方程 有解,则实数
有解,则实数 的取值范围是 ;
的取值范围是 ;
10.某校高中生有900人,其中高一年级300人,高二年级200人,高三年级400人,现采取分层抽样法抽取容量为45人的样本,那么高一、高二、高三年级抽取的人数分别为 ;
9..现从某校5名学生中选出3分别参加高中“数学”“物理”“化学”竞赛,要求每科至少有1人参加,且每人只参加1科竞赛,则不同的参赛方案的种数是 ;
8.直线 必过定点
必过定点
A. B.
B.
 C.
C.  D.
D. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com