19.(本题满分14分)

已知函数，其中为实数.

(Ⅰ)若在处取得的极值为，求的值；

(Ⅱ)若在区间上为减函数，且，求的取值范围

18.(本小题满分14分)

如图，平行四边形中，，将

沿折起到的位置，使平面平面

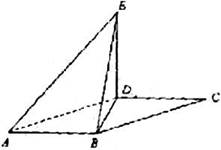　 (I)求证：　　　　　 　　　　　

　 (Ⅱ)求三棱锥的侧面积。

17．(本小题满分12分)

一个袋子中有蓝色球个，红、白两种颜色的球若干个，这些球除颜色外其余完全相同.

(1)甲从袋子中随机取出1个球，取到红球的概率是 ，放回后乙取出一个球，取到白球的概率是，求红球的个数；

(2)从袋子中取出4个红球，分别编号为1号、2号、3号、4号.将这四个球装入一个盒子中，甲和乙从盒子中各取一个球(甲先取，取出的球不放回)，求两球的编号之和不大于的概率．

16．(本小题共12分)已知函数.

(Ⅰ)求的最小正周期；

(Ⅱ)求在区间上的最大值和最小值.

(一)必做题(11--13题)

11．(1)教育局督学组到学校检查工作，需在学号为0001-1000的高三年级的学生中抽调20人参加学校管理的综合座谈会；(2)该校高三年级这1000名学生参加2009年新年晚会，要产生20名“幸运之星”；(3)该校高三年级1000名学生一摸考试的数学成绩有240人在120分以上(包括120分)，600人在120分以下90分以上(包括90分)，其余在90分以下，现欲从中抽取20人研讨进一步改进数学教与学的座谈会. 用如下三种抽样方法：①简单随机抽样 ②系统抽样　 ③分层抽样 选取样本，则以上三件事，最合理的抽样方法序号依次为　　　　　　　　　 .

12．设变量满足约束条件则目标函数的最大值为　　　

13．函数的图像在点M处的切线方程是,=　　　 。(二)选做题(14、15题，考生只能从中选作一题)

14．(坐标系与参数方程选做题)若直线(为参数)与直线平行，

则常数=________.

15．(几何证明选讲选做题)如图4，是圆外一点，过引

圆的两条割线、，，，

则___________．　　　

10．对于任意x、y，定义运算，其中a、b、c是常数，等式右边的运算是通常的加法和乘法运算。现已知，并且有一个非零实数m，使得对于任意实数x，都有，则m的值是(　 )

A．1　　　　 B．2　　　　 C．3　　 　　　D．4

9． 设椭圆的右焦点与抛物线的焦点相同，离心率为，则此椭圆的方程为(　　　 )　

A． 　　　　 B．　 　 C．　　　　　 D．

8．有如下一些说法，其中正确的是 (　　 )

①若直线∥，在面内，则∥；②若直线∥，在面内，则∥；

③若直线∥，∥，则∥；④若直线∥，∥，则∥.

　　　 A．①④ 　　　 B．①③　　　 　 C．②　 　　　 D．均不正确

7．若等差数列满足，则的值是(　　 )

A．20　　　　 　B．24　　　　　 C．36　　　　　　 D．72

6．过点P(0,1)与圆相交的所有直线中，被圆截得的弦最长时的直线方程是(　　　 )

A．x=0　　　 B．y=1　　　 　C．x+y-1=0　　　 D．x-y+1=0