3. 观察下列图形：

　　 如果第x行共有y枚黑白两色围棋子，那么y与x之间的函数关系式是____________。(不要求写出x的取值范围)

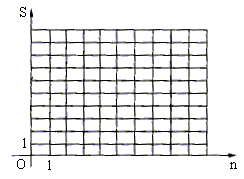
2. 把棱长为a的小正方体按照如图所示的方法摆放，自上而下分别叫第一层、第二层、……、第n层的小正方体的个数记为S。

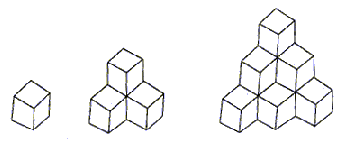
　　 请解答下列问题：

　　 (1)在表中空白处填上适当数字：

　　 (2)写出当时，S＝__________；

　　 (3)根据上表中的数据，把S作为纵坐标，n作为横坐标，在平面直角坐标系中描出相应的各点，并用平滑曲线连接各点；

　 (4)请你猜一猜上述各点会在某个二次函数图象上吗？如果在某个二次函数图像上，求出该函数的解析式(不要求写出自变量n的取值范围；如果不在，请说明理由。

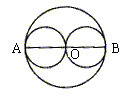
1. 如图，AB是⊙O的直径，把AB分成几条相等的线段，以每条线段为直径分别画小圆，设AB＝a，那么⊙O的周长。

　　 计算：(1)把AB分成两条相等的线段，每个小圆的周长。

　　 (2)把AB分成三条相等的线段，每个小圆的周长__________。

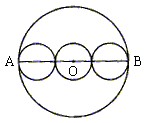
　　 (3)把AB分成四条相等的线段，每个小圆的周长__________。

　　 ……

　　 (4)把AB分成n条相等的线段，每个小圆的周长__________。

　　 结论：把大圆的直径分成n条相等的线段，以每条线段为直径分别画小圆，那么每个小圆周长是大圆周长的___________。

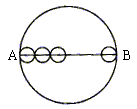
　　 (5)请仿照上面的探索方法和步骤，计算推导出每个小圆面积与大圆面积的关系。

2. 自主探索、合作交流和动手实践有机结合，养成对结果反思的好习惯。

[典型例题]

　 例1. 如图，已知AB是⊙O中一条长为4的弦，P为⊙O上一动点，

出这个三角形的面积；若不存在，请说明理由。

　　 评析：本例“是否存在”的对象是三角形，要求满足“面积最大”的条件。解题的思路是：假定这个三角形存在，则任意画出这个假设的三角形，这时可以发现这个三角形的底是定值，其面积大小取决于高，从而将问题转化到三角形高的最值问题(线段最值)。

　　 假设存在以A、P、B为顶点且面积最大的三角形(任意画出△ABP进行分析)，作PD⊥AB于点D，则PD为弓形的高。

　　 ∵△ABP的底AB是定值，所以其面积大小取决于高PD

　　 显然点P为优弧中点，连结PA、PB，则等腰三角形△APB即为所求。

　　 为了求PD的长，作直径AC，连结BC，则∠C＝∠APB

　 例2. 如图，在Rt△ABC中，∠C＝90°，沿过点B的直线BE折叠这个三角形，要使点C恰好与AB的中点D重合，还应添加什么条件？

　 　评析：本题属条件开放型探究题。如果不再添加辅助线，要使D为AB的中点，可添加下列条件之一：

　　 (1)∠BED＝∠DEA

　　 (2)∠EBA＝∠A

　　 (3)∠AED＝∠CEB

　　 (4)∠A＝∠EBC

　　 (5)∠CEB＝60°

　　 (6)∠DEB＝60°

　　 (7)∠DEA＝60°

　　 (8)∠BEA＝120°

　　 (9)∠EBC＝30°

　　 (10)∠EBA＝30°

　　 (11)∠A＝30°

　　 (12)∠CBA＝60°(以上是角的关系)

　　 (13)BE＝AE

　　 (14)AB＝2BC

　　 (17)△BEC≌△AED(三角形之间关系)

　　 由于本题添加的条件属性不明，可以从不同角度、不同层次回答，因此答案繁多。虽然从理论上讲，本题的答案是有限个，但实际上，解题者很难一下子把所有答案一一列举出来。我们把这一类的条件开放题称为有限混浊型条件开放探究题。解这类题的策略是：需从多个不同角度思考，先从直接条件入手，再挖间接的、隐含的条件，并按某些规律分类表述。如本题先从角的关系来表述，再从边的关系表述，最后是从三角形之间的关系来表述，这样就容易做到不重不漏。

　 例3. 已知：如图，菱形ABCD中，∠B＝60°，是否存在另一个菱形，它的周长和面积分别是已知菱形周长和面积的2倍？请你写出自己的探究过程。

　 　分析：此题为存在型的探究题，如果存在的话，只要找到一个符合条件的菱形就可以得出结论。如果是不存在的话，就要说明理由了。

　 　答：存在。

　　 设菱形ABCD边长为a，面积为s；另一个菱形为A₁B₁C₁D₁，边长＝b，面积＝S，过A做AE⊥BC于E，过A₁E₁⊥B₁C₁，C＝4a，C₁＝2C

　　 存在另一个菱形，其周长和面积是已知菱形周长和面积的2倍，菱形A₁B₁C₁D₁的边长是菱形ABCD边长的2倍，∠B₁≈25.7°。

　 例4. 某商厦张贴巨幅广告：“真情回报顾客”活动共设奖金20万元，最高奖每份1万元，平均每份奖金200元，一顾客幸运地抽到一张奖券，奖金数为10元，她调查了周围正兑奖的其他顾客，一个也没有超过50元的，她气愤地要求与商厦领导评理。商厦领导说不存在欺骗，并向她出示了下面这张奖金分配表，你认为商厦说“平均每份奖金200元”是否欺骗了顾客？大多数中奖者获得的奖金能接近奖金的平均数吗？中一等奖的概率是多少？以后遇到开奖的问题你应该更关心什么？

　 　分析：平均数、众数、中位数这三个统计量都是反映数据集中程度的统计量。由于每个等级设置的中奖人数差距悬殊，90%的奖券金额不超过50元，因此中奖者获得的奖金大多不能用平均数来衡量。对于开奖的问题应选择的统计量是众数。

　 　解：

　　 即平均每份奖券的奖金确为200元，没有欺骗顾客。

以后遇到开奖的问题，应该更关心中奖金额的众数等信息。

　 例5. 从鄂州到武汉有新旧两条公路可走，一辆最多可乘19人的汽车在这条公路上行驶时有关数据如下表：

　　 说明：1升/100千米表示汽车每行驶100千米耗油1升。

　　 (1)如果用y₁(元)、y₂(元)分别表示汽车从鄂州到武汉走新路、旧路时司机的收入，仅就上表数据求出y₁、y₂与载客人数x(人)之间的函数关系式；

　　 (2)你认为司机应选择哪条公路才能使收入较多？

　　 评析：表式信息的优越性就在于将所有的已知数量的对应关系显现了出来，但它反映的仅仅是对应关系，还需要找到这些数量之间的等量关系，如本例只有找到关系式：

　　 司机的收入＝人数×票价－路程×耗油量×油价－过路费

　　 才能解决(1)的问题：

　　 要解决(2)的问题，需要比较y₂和y₁的大小。

　　 其中x是不超过19的正整数。

　　 即当乘车人数不到4人时，y₂＞y₁，走旧路比走新路司机收入多；

　　 当乘车人数是4人或超过4人时，y₂＜y₁，走新路比走旧路司机收入多。

1. 采用多样化的方式学习，体验实际生活与数学的密切联系，提高用数学的意识。

2. 加深对“数与代数”“空间与几何”“统计与概率”内容的理解，体会各部分知识之间的联系，能针对不同的探究题目采取有效的解题策略。

1. 综合运用已有的知识和经验，经过自主探索和合作交流，解决与生活经验密切联系的、具有挑战性和综合性的问题，发展解决问题的能力。

　　 例6　 如图，在方格内已填好了两个数19和95，可以在其余的方格中填上适当的数，使每一行、每一列、以及每一条对角线上的三个数的和都相等，

　　 (1)求x；

　　 (2)在题设的基础上，如果中间的空格上是100，请完成填图。

　　 解：(1)设每一行、每一列、每一条对角线的三个数都相等的数是k

　　 (2)中间填上100，从而不难求每行、每列、每条对角线的三个数的和为300，则其余空格上数字如图。

　　 例5　 对应实数x,y，设，等式右边是通常的加法和乘法，且

　　 解：由题意，得

　　 例1　 对于任意实数m，等式

　　 解：

　　 例2　 关于x的代数式，当x分别取1,2,-1时，y的值分别是4，7，10，求a,b,c的值。

　　 解：根据题意，得

　　 例3　 已知都是关于x,y的某个二元一次方程的解，求这个二元一次方程。

　　 解：设这个二元一次方程为

　　 例4　 已知等式

　　 解：由已知条件得

　　 比较对应项的系数，得