
11.一个直流电源的电动势为正,内电阻为r,电源的电动势和内电阻保持不变。R1和R2为两个定值电阻,图9是在同一坐标系中画出的它们的U-I图线。从图线可以看出,两个电阻相比, 的阻值较大,并可得出R1= Ω。若将R1,接在该电源的两极问,电源的输出功率为 W。
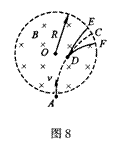
10. 如图8所示,在一个半径为及的圆形区域内存在着匀强磁
场,磁场方向垂直于圆面向里。一个带电粒子从磁场边界的A点
以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场
边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点
的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的
运动情况,以下判断正确的是 ( )
A.新粒子的运动半径将减小,可能到达F点
B.新粒子的运动半径将增大,可能到达E点
C.新粒子的运动半径将不变,仍然到达C点
D.新粒子在磁场中的运动时间将变长
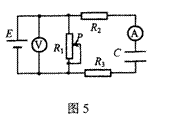
7.在如图5所示的电路中,电源电动势为E。设电流表的
示数为I,电压表的示数为U,电容器C所带的电荷量为Q。
将滑动变阻器R1的滑动触头P向上移动,待电流达到稳定后,
则与P移动前相比 ( )
A.若电源内阻不可忽略,则U减小
B.若电源内阻不可忽略,则I增大
C.若电源内阻不可忽略,则Q减小
D.若电源内阻可以忽略,则Q减小
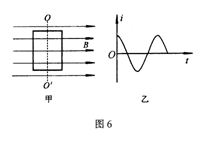 8.如图6甲所示,一矩形闭合线圈在匀
8.如图6甲所示,一矩形闭合线圈在匀
强磁场中绕垂直于磁场方向的转轴OO′以恒
定的角速度ω转动,当线圈平面与磁场方向
平行时开始计时,线圈中产生的交变电流按
照图乙所示的余弦规律变化。在t=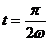 时刻
时刻
( )
A.线圈中的电流最大
B.穿过线圈的磁通量为零
C.线圈所受安培力的力矩为零
D.线圈消耗的电功率为零
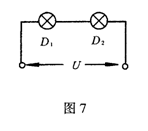 9.如图7所示,两只相同的白炽灯泡D1和D2串联后接在电
9.如图7所示,两只相同的白炽灯泡D1和D2串联后接在电
压恒定的电路中。若D1的灯丝断了,经过搭丝后(搭丝后灯泡的
电阻减小)仍然与D2串联,重新接人原来的电路。假设在此过程
中,灯丝电阻随温度变化的因素可忽略不计,且每只灯泡两端的电
压均未超过其额定电压。则此时每只灯泡所消耗的功率与原来各自
的功率相比,有 ( )
A.D1的功率变大 B.Dl的功率变小
 C.D2的功率变大 D.D2的功率变小
C.D2的功率变大 D.D2的功率变小
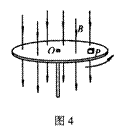
6.如图4所示,在一个水平胶木圆盘上有一个带负电荷的金
属块P随圆盘一起绕过O点的竖直轴匀速转动,圆盘转动的最大
角速度为ω。若在竖直方向加一向下的匀强磁场,仍然保持P随圆
盘一起转动,圆盘依图示方向匀速转动的最大角速度为ω′。则下
面判断正确的是 ( )
A.金属块受到的磁场力方向指向圆心O
B.金属块受到的磁场力方向背离圆心O
C.ω〈ω′
 D.ω〉ω′
D.ω〉ω′
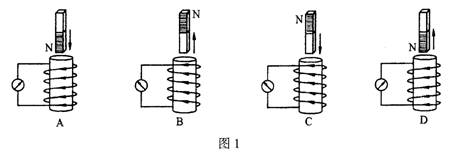
3.图1是验证楞次定律实验的示意图,竖直放置的线圈固定不动,将磁铁从线圈上方插入或拔出,线圈和电流表构成的闭合回路中就会产生感应电流。各图中分别标出了磁铁的极性、磁铁相对线圈的运动方向以及线圈中产生的感应电流的方向等情况,其中表示正确的是 ( )
 4.图2画出了匀强电场中的几条电场线,M、N是该电场中的两
4.图2画出了匀强电场中的几条电场线,M、N是该电场中的两
点。一个带正电荷的离子(不计重力)仅在电场力的作用下由M点运动
到N点,则 ( )
A.该离子在M点的速度不为零
B.该离子在M点的速度可能为零
C.该离子在M点的电势能大于在N点的电势能
D.该离子在M点的电势能小于在N点的电势能
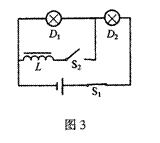 5.在如图3所示的电路中,Dl和D2是两个完全相同的灯泡,
5.在如图3所示的电路中,Dl和D2是两个完全相同的灯泡,
其额定电压在数值上约等于电源电动势,电源内电阻可以忽略不
计,L是一个自身电阻可以忽略不计而自感系数足够大的线圈。将
开关S2断开、S1闭合,两个灯泡都发出较暗的光。若闭合S2,两
个灯的亮度变化情况是 ( )
A.D1逐渐变亮,后来亮度稳定
B.D1逐渐变暗,后来熄灭
C.D2逐渐变亮,后来亮度稳定
 D.D2逐渐变暗,后来熄灭
D.D2逐渐变暗,后来熄灭
2.在一个密闭的容器里有一定质量的理想气体,在气体的温度升高,而体积保持不变的过程中 ( )
A.气体分子热运动的平均动能增大 B.气体从外界吸收热量
C. 外界对气体做功 D.气体的内能增大
1.关于电场和磁场的概念,以下说法正确的是 ( )
A.电荷放人电场中某区域内的任意位置,电荷受到的电场力都相同,则该区域内的电场一定是匀强电场
B.放人电场中某位置的电荷受到的电场力不为零,则该位置的电场强度一定不为零
C.电荷在磁场中某位置受到的磁场力为零,则该位置的磁感应强度一定为零
D.一小段通电导体在磁场中某位置受到的磁场力为零,则该位置的磁感应强度一定为零
24.如图,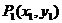 、
、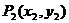 、…、
、…、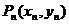
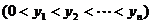 是曲线
是曲线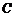 :
: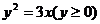 上的
上的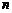 个点,点
个点,点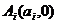 (
(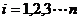 )在
)在 轴的正半轴上,且
轴的正半轴上,且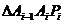 是正三角形(
是正三角形(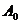 是坐标原点).
是坐标原点).
(1)写出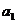 、
、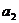 、
、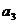 ;
;
(2)求出点 (
(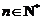 )
) 的
的
横坐标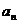 关于
关于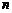 的表达式并证明.
的表达式并证明.
解:(Ⅰ)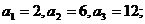 ……………….6分
……………….6分
(2)依题意,得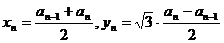 ,由此及
,由此及 得
得
 ,
,
即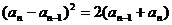 .
.
由(Ⅰ)可猜想: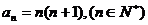 .
.
下面用数学归纳法予以证明:
(1)当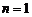 时,命题显然成立;
时,命题显然成立;
(2)假定当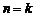 时命题成立,即有
时命题成立,即有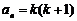 ,则当
,则当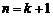 时,由归纳假设及
时,由归纳假设及
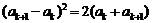
得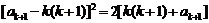 ,即
,即
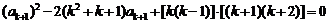 ,
,
解之得
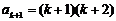 (
( 不合题意,舍去),
不合题意,舍去),
即当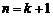 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立.……………….10分
23.解: 分析:由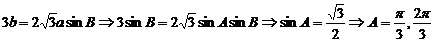 [来源:]
[来源:]
由
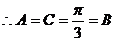
所以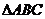 为等边三角形
为等边三角形
22. 三个方程中都没有两个相异实根
证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
方法总结:反证法步骤-假设结论不成立→推出矛盾→假设不成立.
凡是“至少”、“唯一”或含有否定词的命题适宜用反证法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com