
20. (本小题满分14分)
已知函数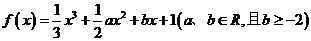 ,当
,当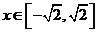 时,总有
时,总有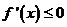 。
。
(1)求函数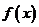 的解析式;
的解析式;
(2)设函数 ,求证:当
,求证:当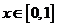 时,若
时,若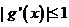 恒成立,则
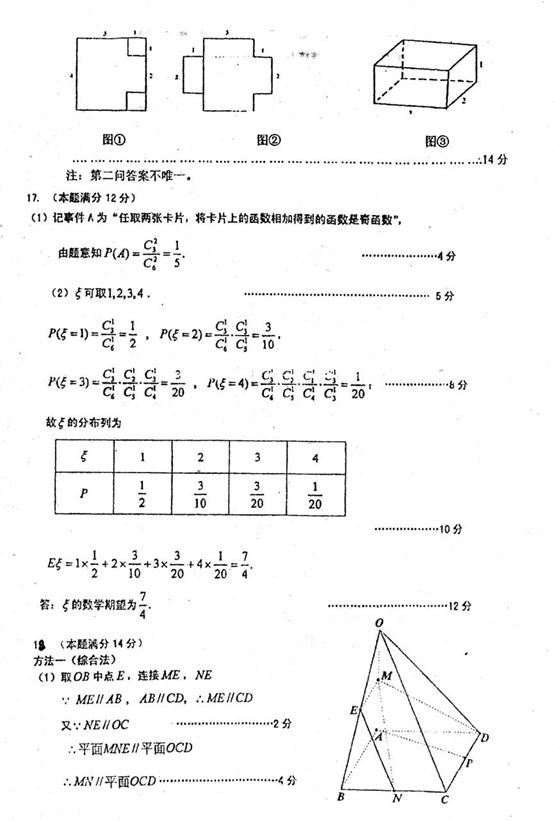
恒成立,则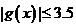 也恒成立。
也恒成立。




19. (本题满分14分)
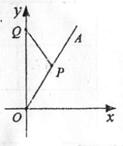
如右图所示,在直角坐标系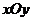 中,射线
中,射线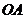 在第一象限,且与
在第一象限,且与 轴的正半轴成定角60°,动点
轴的正半轴成定角60°,动点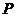 在射线
在射线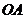 上运动,动点
上运动,动点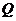 在
在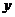 轴的正半轴上运动,
轴的正半轴上运动,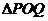 的面积为
的面积为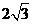 。
。
 (I)求线段
(I)求线段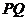 中点
中点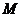 的轨迹
的轨迹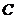 的方程;
的方程;
(II)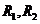 是曲线
是曲线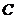 上的动点,
上的动点,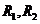 到
到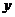 轴的距离之和为1,设
轴的距离之和为1,设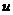 为
为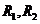 到
到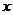 轴的距离之积。问:是否存在最大的常数
轴的距离之积。问:是否存在最大的常数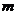 ,使
,使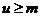 恒成立?若存在,求出这个
恒成立?若存在,求出这个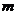 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
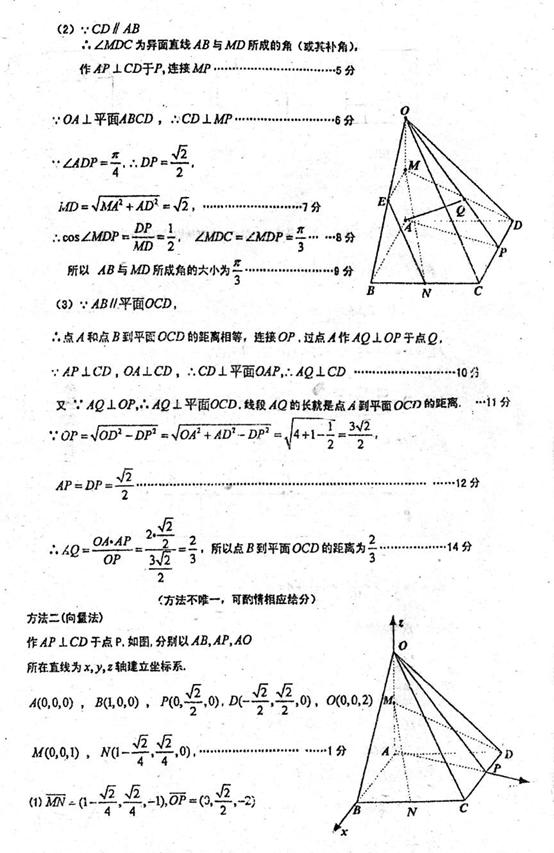
18. (本题满分14分)
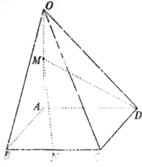 如图,在四棱锥
如图,在四棱锥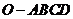 中,底面
中,底面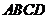 是边长为1的菱形,
是边长为1的菱形,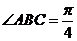 ,
,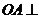 底面
底面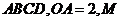 为
为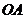 的中点,
的中点,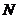 为
为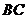 的中点。
的中点。
(I)证明:直线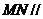 平面
平面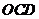 ;
;
(II)求异面直线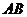 与
与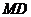 所成角的大小;
所成角的大小;
(III)求点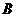 到平面
到平面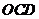 的距离。
的距离。
17. (本题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为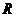 的函数:
的函数:
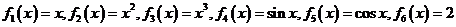
(I)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(II)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数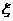 的分布列和数学期望。
的分布列和数学期望。
16. (本小题满分14分)
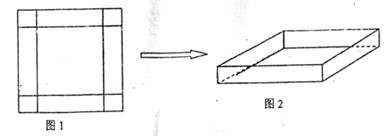
在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的成方体无盖容器(只有一个下底面和侧面的长方体),该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2),请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求答方案,简单说明操作过程和理由。
15. (本题满分12分)
已知函数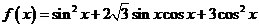
(I)求函数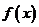 的最小正周期及单调地增区间;
的最小正周期及单调地增区间;
(II)已知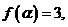 且
且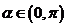 ,求
,求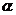 的值。
的值。
14. 已知参数方程
已知参数方程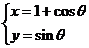 ,(参数
,(参数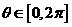 ,则该曲
,则该曲
线上的点与定点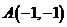 的距离的最小值是
。
的距离的最小值是
。
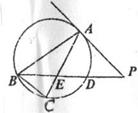
13. 如图,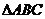 是圆
是圆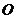 的内接三角形,
的内接三角形,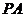 是圆
是圆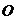 的切线,
的切线,
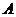 为切点,
为切点,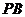 交
交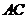 于点
于点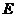 ,交圆
,交圆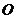 于点
于点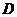 ,若
,若
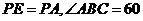 °,且
°,且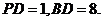 则
则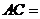
12. 将1,2,3,…,100这100个自然数任意分成50组,每
组两个数,现将每组的两个数中任意一个记为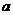 ,另一个
,另一个
数记为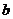 ,按右框图所示进行运算(注:框图中每次“输
,按右框图所示进行运算(注:框图中每次“输
入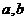 ”为同一组的
”为同一组的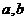 值,其每组数据不重复输入),则
值,其每组数据不重复输入),则
输出的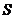 最大值为
;
最大值为
;
11. 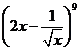 的展开式中,常数项为
;(用数
的展开式中,常数项为
;(用数
字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com