
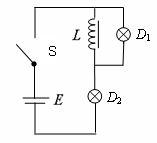
4.如图所示,E为电池,L是直流电阻可忽略不计、自感系数足够大的线圈,D1、D2是两个完全相同的灯泡,S是控制电路的开关。对于这个电路,下列说法正确的是 ( )
A.刚闭合S的瞬间,灯泡D1、D2的亮度相同
B.刚闭合S的瞬间,灯泡D2比灯泡 D1亮
C.闭合S待电路达到稳定后,D1熄灭,D2比S刚闭合时亮
D.闭合S待电路达到稳定后,再将S断开瞬间,D2立即熄灭,D1比S刚闭合时亮
3.线圈在匀强磁场中匀速转动,产生交变电流的图象如图所示,由图可知( )
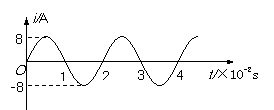 A.t=0.01s时线圈处于中性面位置,穿过
A.t=0.01s时线圈处于中性面位置,穿过
线圈的磁通量为零
B.t=0.015s时线圈处于中性面位置,穿
过线圈的磁通量为零
C.该交变电流的有效值为8A,频率为
50Hz
 D.该交变电流的有效值为4
D.该交变电流的有效值为4 A,频率为50Hz
A,频率为50Hz
2.三个电子各具有与磁场方向垂直的速度v、2v、3v,则它们在同一匀强磁场中回旋的半径之比和频率之比为( )
A.1∶2∶3,1∶2∶3 B.1∶2∶3,1∶1∶1
C.1∶1∶1,1∶2∶3 D.1∶1∶1,1∶1∶1
1.在美丽的松花江畔,位于吉林市南部24公里处,坐落着我国最早建成的大型水电站--丰满发电厂。宏伟的拦江大坝,高耸的输电铁塔,清丽的湖光山色,构成了一幅极富神韵的画卷。在丰满发电厂向长春市远距离输电中,当输送的电功率为P,输送电压为U时,输电线上损失的电功率是 ,若输送的电功率增加为4P,而输电线中损失的电功率减为
,若输送的电功率增加为4P,而输电线中损失的电功率减为 ,那么输电电压应增为( )
,那么输电电压应增为( )
A.32U B.16U C.8U D.4U
纵观针对本专题的高考题目,本专题考察具有以下特点:
从内容来看,高考侧重于对主干知识的考查:尊重客观规律与发挥主观能动性的关系;认识世界和改造世界;主观能性的主、客观制约因素;现象与本质、感性认识和理性认识;真理是人们对事物本质及其发展规律的正确认识;认识的根本任务是使感性认识上升到理性认识,透过现象看本质;分析与综合相结合;合理想象、创造性思维;实践的基本特征;实践与认识的辩证关系。
从能力看,侧重于对获取试题提供的信息、运用相关学科的知识原理分析问题、综合运用相关学科的原理和方法论证和探讨问题等能力的考查。其中非选择题综合性较强,涉及到的能力层次较多较高。
从形式上看,试题背景多选用社会生活中的典型事例或名言警句,非选择题多结合国家社会重大热点问题,命题形式多样,选择题和非选择题分量大体相同。
因此,在复习时,在注意深入把握基本知识、基本原理的基础上,还要特别注意和唯物论、辩证法的有机结合和宏观把握。
8. “分期付款”、“森林木材”型应用问题
(1)这类应用题一般可转化为等差数列或等比数列问题.但在求解过程中,务必“卡手指”,细心计算“年限”.对于“森林木材”既增长又砍伐的问题,则常选用“统一法”统一到“最后”解决.
(2)利率问题:①单利问题:如零存整取储蓄(单利)本利和计算模型:若每期存入本金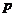 元,每期利率为
元,每期利率为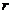 ,则
,则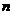 期后本利和为:
期后本利和为: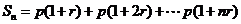
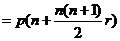 (等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)
(等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)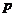 元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分
元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分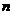 期还清。如果每期利率为
期还清。如果每期利率为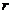 (按复利),那么每期等额还款
(按复利),那么每期等额还款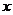 元应满足:
元应满足: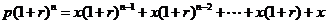 (等比数列问题).
(等比数列问题).
7.数列求和的常用方法:
(1)公式法:①等差数列求和公式;②等比数列求和公式,特别声明:运用等比数列求和公式,务必检查其公比与1的关系,必要时需分类讨论.;③常用公式: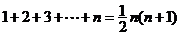 ,
,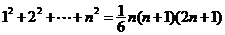 ,
,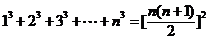 .如(1)等比数列
.如(1)等比数列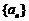 的前
的前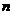 项和Sn=2n-1,则
项和Sn=2n-1,则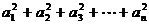 =_____(答:
=_____(答: );(2)计算机是将信息转换成二进制数进行处理的。二进制即“逢2进1”,如
);(2)计算机是将信息转换成二进制数进行处理的。二进制即“逢2进1”,如 表示二进制数,将它转换成十进制形式是
表示二进制数,将它转换成十进制形式是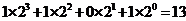 ,那么将二进制
,那么将二进制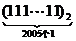 转换成十进制数是_______(答:
转换成十进制数是_______(答: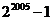 )
)
(2)分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用公式法求和. 如求: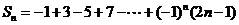 (答:
(答: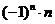 )
)
(3)倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考虑选用倒序相加法,发挥其共性的作用求和(这也是等差数列前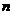 和公式的推导方法). 如①求证:
和公式的推导方法). 如①求证: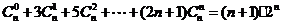 ;②已知
;②已知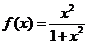 ,则
,则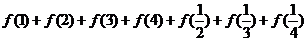 =______(答:
=______(答: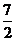 )
)
(4)错位相减法:如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选用错位相减法(这也是等比数列前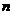 和公式的推导方法). 如(1)设
和公式的推导方法). 如(1)设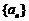 为等比数列,
为等比数列,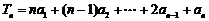 ,已知
,已知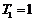 ,
,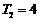 ,①求数列
,①求数列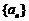 的首项和公比;②求数列
的首项和公比;②求数列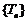 的通项公式.(答:①
的通项公式.(答:①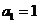 ,
,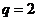 ;②
;②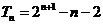 );(2)设函数
);(2)设函数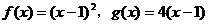 ,数列
,数列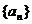 满足:
满足: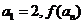
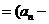
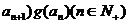 ,①求证:数列
,①求证:数列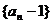 是等比数列;②令
是等比数列;②令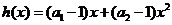
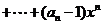 ,求函数
,求函数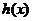 在点
在点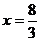 处的导数
处的导数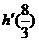 ,并比较
,并比较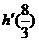 与
与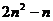 的大小。(答:①略;②
的大小。(答:①略;②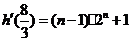 ,当
,当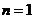 时,
时,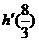 =
=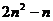 ;当
;当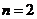 时,
时,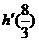 <
<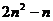 ;当
;当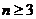 时,
时,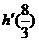 >
>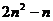 )
)
(5)裂项相消法:如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂项相消法求和.常用裂项形式有:
①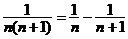 ; ②
; ②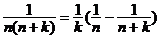 ;
;
③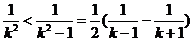 ,
,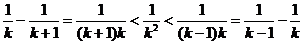 ;
;
④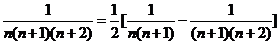 ;⑤
;⑤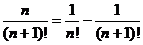 ;
;
⑥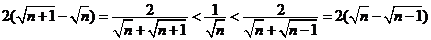 .
.
如(1)求和: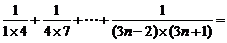 (答:
(答: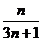 );(2)在数列
);(2)在数列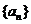 中,
中,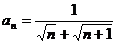 ,且Sn=9,则n=_____(答:99);
,且Sn=9,则n=_____(答:99);
(6)通项转换法:先对通项进行变形,发现其内在特征,再运用分组求和法求和。如①求数列1×4,2×5,3×6,…,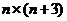 ,…前
,…前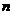 项和
项和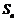 = (答:
= (答: );②求和:
);②求和: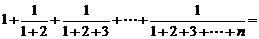 (答:
(答: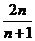 )
)
6.数列的通项的求法:
⑴公式法:①等差数列通项公式;②等比数列通项公式。如已知数列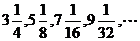 试写出其一个通项公式:__________(答:
试写出其一个通项公式:__________(答: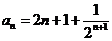 )
)
⑵已知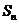 (即
(即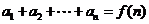 )求
)求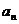 ,用作差法:
,用作差法: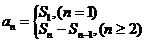 。如①已知
。如①已知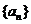 的前
的前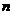 项和满足
项和满足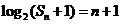 ,求
,求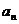 (答:
(答: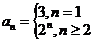 );②数列
);②数列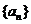 满足
满足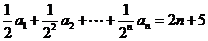 ,求
,求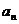 (答:
(答: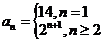 )
)
⑶已知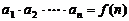 求
求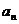 ,用作商法:
,用作商法: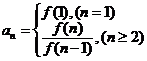 。如数列
。如数列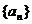 中,
中,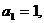 对所有的
对所有的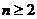 都有
都有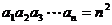 ,则
,则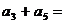 ______(答:
______(答: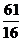 )
)
⑷若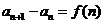 求
求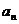 用累加法:
用累加法:
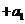
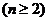 。如已知数列
。如已知数列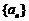 满足
满足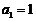 ,
,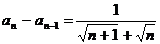
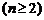 ,则
,则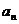 =________(答:
=________(答: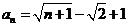 )
)
⑸已知 求
求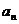 ,用累乘法:
,用累乘法: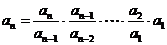
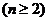 。如已知数列
。如已知数列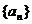 中,
中,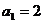 ,前
,前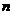 项和
项和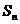 ,若
,若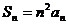 ,求
,求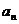 (答:
(答: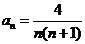 )
)
⑹已知递推关系求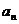 ,用构造法(构造等差、等比数列)。特别地,(1)形如
,用构造法(构造等差、等比数列)。特别地,(1)形如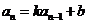 、
、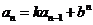 (
(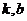 为常数)的递推数列都可以用待定系数法转化为公比为
为常数)的递推数列都可以用待定系数法转化为公比为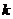 的等比数列后,再求
的等比数列后,再求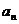 。如①已知
。如①已知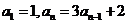 ,求
,求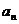 (答:
(答: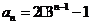 );②已知
);②已知 ,求
,求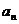 (答:
(答: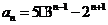 );(2)形如
);(2)形如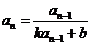 的递推数列都可以用倒数法求通项。如①已知
的递推数列都可以用倒数法求通项。如①已知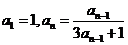 ,求
,求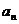 (答:
(答: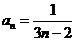 );②已知数列满足
);②已知数列满足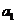 =1,
=1,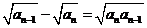 ,求
,求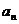 (答:
(答: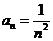 )
)
注意:(1)用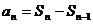 求数列的通项公式时,你注意到此等式成立的条件了吗?(
求数列的通项公式时,你注意到此等式成立的条件了吗?(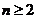 ,当
,当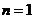 时,
时,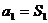 );(2)一般地当已知条件中含有
);(2)一般地当已知条件中含有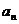 与
与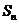 的混合关系时,常需运用关系式
的混合关系时,常需运用关系式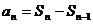 ,先将已知条件转化为只含
,先将已知条件转化为只含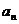 或
或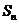 的关系式,然后再求解。如数列
的关系式,然后再求解。如数列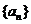 满足
满足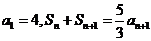 ,求
,求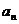 (答:
(答: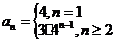 )
)
5.等比数列的性质:
(1)当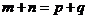 时,则有
时,则有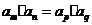 ,特别地,当
,特别地,当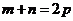 时,则有
时,则有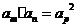 .如(1)在等比数列
.如(1)在等比数列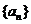 中,
中,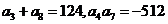 ,公比q是整数,则
,公比q是整数,则 =___(答:512);(2)各项均为正数的等比数列
=___(答:512);(2)各项均为正数的等比数列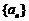 中,若
中,若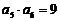 ,则
,则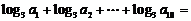 (答:10)。
(答:10)。
(2) 若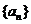 是等比数列,则
是等比数列,则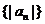 、
、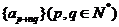 、
、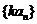 成等比数列;若
成等比数列;若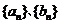 成等比数列,则
成等比数列,则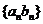 、
、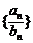 成等比数列; 若
成等比数列; 若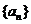 是等比数列,且公比
是等比数列,且公比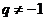 ,则数列
,则数列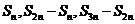 ,…也是等比数列。当
,…也是等比数列。当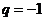 ,且
,且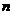 为偶数时,数列
为偶数时,数列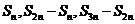 ,…是常数数列0,它不是等比数列. 如(1)已知
,…是常数数列0,它不是等比数列. 如(1)已知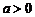 且
且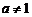 ,设数列
,设数列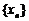 满足
满足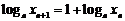
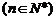 ,且
,且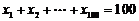 ,则
,则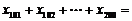 . (答:
. (答: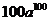 );(2)在等比数列
);(2)在等比数列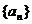 中,
中,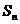 为其前n项和,若
为其前n项和,若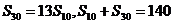 ,则
,则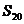 的值为______(答:40)
的值为______(答:40)
(3)若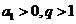 ,则
,则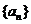 为递增数列;若
为递增数列;若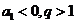 , 则
, 则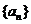 为递减数列;若
为递减数列;若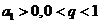 ,则
,则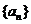 为递减数列;若
为递减数列;若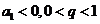 , 则
, 则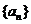 为递增数列;若
为递增数列;若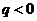 ,则
,则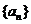 为摆动数列;若
为摆动数列;若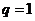 ,则
,则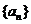 为常数列.
为常数列.
(4) 当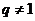 时,
时, ,这里
,这里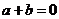 ,但
,但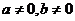 ,这是等比数列前
,这是等比数列前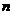 项和公式的一个特征,据此很容易根据
项和公式的一个特征,据此很容易根据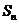 ,判断数列
,判断数列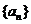 是否为等比数列。如若
是否为等比数列。如若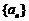 是等比数列,且
是等比数列,且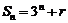 ,则
,则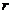 = (答:-1)
= (答:-1)
(5) 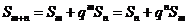 .如设等比数列
.如设等比数列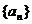 的公比为
的公比为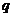 ,前
,前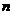 项和为
项和为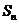 ,若
,若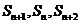 成等差数列,则
成等差数列,则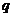 的值为_____(答:-2)
的值为_____(答:-2)
(6) 在等比数列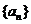 中,当项数为偶数
中,当项数为偶数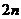 时,
时,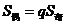 ;项数为奇数
;项数为奇数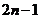 时,
时,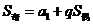 .
.
(7)如果数列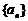 既成等差数列又成等比数列,那么数列
既成等差数列又成等比数列,那么数列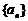 是非零常数数列,故常数数列
是非零常数数列,故常数数列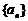 仅是此数列既成等差数列又成等比数列的必要非充分条件。如设数列
仅是此数列既成等差数列又成等比数列的必要非充分条件。如设数列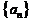 的前
的前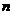 项和为
项和为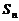 (
(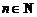 ), 关于数列
), 关于数列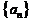 有下列三个命题:①若
有下列三个命题:①若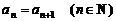 ,则
,则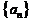 既是等差数列又是等比数列;②若
既是等差数列又是等比数列;②若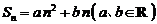 ,则
,则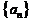 是等差数列;③若
是等差数列;③若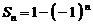 ,则
,则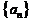 是等比数列。这些命题中,真命题的序号是 (答:②③)
是等比数列。这些命题中,真命题的序号是 (答:②③)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com