7.求函数解析式的常用方法：

(1)待定系数法――已知所求函数的类型(二次函数的表达形式有三种：一般式：；顶点式：；零点式：，要会根据已知条件的特点，灵活地选用二次函数的表达形式)。如已知为二次函数，且 ，且f(0)=1,图象在x轴上截得的线段长为2,求的解析式 。(答：)

(2)代换(配凑)法――已知形如的表达式，求的表达式。如(1)已知求的解析式(答：)；(2)若，则函数=_____(答：)；(3)若函数是定义在R上的奇函数，且当时，，那么当时，=________(答：). 这里需值得注意的是所求解析式的定义域的等价性，即的定义域应是的值域。

(3)方程的思想――已知条件是含有及另外一个函数的等式，可抓住等式的特征对等式的进行赋值，从而得到关于及另外一个函数的方程组。如(1)已知，求的解析式(答：)；(2)已知是奇函数，是偶函数，且+= ,则=　　　 __(答：)。

6.分段函数的概念。分段函数是在其定义域的不同子集上，分别用几个不同的式子来表示对应关系的函数，它是一类较特殊的函数。在求分段函数的值时，一定首先要判断属于定义域的哪个子集，然后再代相应的关系式；分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。如(1)设函数，则使得的自变量的取值范围是__________(答：)；(2)已知，则不等式的解集是________(答：)

5.求函数值域(最值)的方法：

(1)配方法――二次函数(二次函数在给出区间上的最值有两类：一是求闭区间上的最值；二是求区间定(动)，对称轴动(定)的最值问题。求二次函数的最值问题，勿忘数形结合，注意“两看”：一看开口方向；二看对称轴与所给区间的相对位置关系)，如(1)求函数的值域(答：[4,8])；(2)当时，函数在时取得最大值，则的取值范围是___(答：)；(3)已知的图象过点(2,1)，则的值域为______(答：[2, 5])

(2)换元法――通过换元把一个较复杂的函数变为简单易求值域的函数，其函数特征是函数解析式含有根式或三角函数公式模型，如(1)的值域为_____(答：)；(2)的值域为_____(答：)(令，。运用换元法时，要特别要注意新元的范围)；(3)的值域为____(答：)；(4)的值域为____(答：)；

(3)函数有界性法――直接求函数的值域困难时，可以利用已学过函数的有界性，来确定所求函数的值域，最常用的就是三角函数的有界性，如求函数，，的值域(答： 、(0,1)、)；

(4)单调性法――利用一次函数，反比例函数，指数函数，对数函数等函数的单调性，如求，，的值域为______(答：、、)；

(5)数形结合法――函数解析式具有明显的某种几何意义，如两点的距离、直线斜率、等等，如(1)已知点在圆上，求及的取值范围(答：、)；(2)求函数的值域(答：)；(3)求函数及的值域(答：、)注意：求两点距离之和时，要将函数式变形，使两定点在轴的两侧，而求两点距离之差时，则要使两定点在轴的同侧。

(6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用，但这类题型有时也可以用其它方法进行求解，不必拘泥在判别式法上，也可先通过部分分式后，再利用均值不等式：

①型，可直接用不等式性质，如求的值域(答：)

②型，先化简，再用均值不等式，如(1)求的值域(答：)；(2)求函数的值域(答：)

③型，通常用判别式法；如已知函数的定义域为R，值域为[0，2]，求常数的值(答：)

④型，可用判别式法或均值不等式法，如求的值域(答：)

(7)不等式法――利用基本不等式求函数的最值，其题型特征解析式是和式时要求积为定值，解析式是积时要求和为定值，不过有时须要用到拆项、添项和两边平方等技巧。如设成等差数列，成等比数列，则的取值范围是____________.(答：)。

(8)导数法――一般适用于高次多项式函数，如求函数，的最小值。(答：－48)

提醒：(1)求函数的定义域、值域时，你按要求写成集合形式了吗？(2)函数的最值与值域之间有何关系？

4. 求函数定义域的常用方法(在研究函数问题时要树立定义域优先的原则)：

(1)根据解析式要求如偶次根式的被开方大于零，分母不能为零，对数中且，三角形中, 最大角，最小角等。如(1)函数的定义域是____(答：)；(2)若函数的定义域为R，则_______(答：)；(3)函数的定义域是，，则函数的定义域是__________(答：)；(4)设函数，①若的定义域是R，求实数的取值范围；②若的值域是R，求实数的取值范围(答：①；②)

(2)根据实际问题的要求确定自变量的范围。

(3)复合函数的定义域：若已知的定义域为,其复合函数的定义域由不等式解出即可；若已知的定义域为,求的定义域，相当于当时，求的值域(即的定义域)。如(1)若函数的定义域为，则的定义域为__________(答：)；(2)若函数的定义域为，则函数的定义域为________(答：[1,5])．

3. 同一函数的概念。构成函数的三要素是定义域，值域和对应法则。而值域可由定义域和对应法则唯一确定，因此当两个函数的定义域和对应法则相同时，它们一定为同一函数。如若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“天一函数”，那么解析式为，值域为{4，1}的“天一函数”共有______个(答：9)

2.函数: AB是特殊的映射。特殊在定义域A和值域B都是非空数集！据此可知函数图像与轴的垂线至多有一个公共点，但与轴垂线的公共点可能没有，也可能有任意个。如(1)已知函数，，那么集合中所含元素的个数有　　　 个(答： 0或1)；(2)若函数的定义域、值域都是闭区间，则＝　　　 (答：2)

1.映射: AB的概念。在理解映射概念时要注意：⑴A中元素必须都有象且唯一；⑵B中元素不一定都有原象，但原象不一定唯一。如(1)设是集合到的映射，下列说法正确的是　A、中每一个元素在中必有象　　 B、中每一个元素在中必有原象　C、中每一个元素在中的原象是唯一的 　D、是中所在元素的象的集合(答：A)；(2)点在映射的作用下的象是，则在作用下点的原象为点________(答：(2，－1))；(3)若，，，则到的映射有　　 个，到的映射有　 个，到的函数有　　 个(答：81,64,81)；(4)设集合，映射满足条件“对任意的，是奇数”，这样的映射有____个(答：12)；(5)设是集合A到集合B的映射，若B={1,2}，则一定是_____(答：或{1}).

(五)计算题

43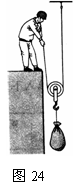．如图24所示，一人用100N的拉力使用动滑轮将重为180N的物体向上提起，绳重和摩擦不计.在拉力的作用下，物体匀速上升了1m 。

求：①人克服重力所做的功；　　

②拉力所做的功；　　

③动滑轮的机械效率.

44．用如图25所示的滑轮组来匀速拉动钢锭，已知钢锭与地面的摩擦力F₁为

1200N，若此时滑轮组的机械效率为80%，物体速度为1m/s．

①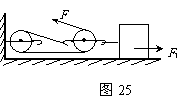拉绳的速度是多少？

②拉绳的力F至少为多大？

③拉力的功率是多少？

④如果想用更小的力拉动钢锭，请你提出一条可行性建议．

45．2008年北京残奥会开幕式最后一棒火炬手侯斌，靠自己双手的力量，攀爬到火炬台底部并最终点燃圣火，该点火仪式充分体现了残疾人自强自立、拼搏向上的勇气和精神.已知他和轮椅总质量为80kg，攀爬高度39m，历时约3min20s.

(1)如果不计机械装置的额外功，求他的平均功率是多大？

(2)小明同学看到火炬手攀爬很费劲，想到物理课上学过利用滑轮组可以省力.小明同学如果站在地面上,用如图26所示的哪个滑轮组拉起火炬手侯斌最合适,理由是什么? 如果该滑轮组机械效率为80%，求小明同学的拉力至少要多大？(g取10N/kg)

(四)实验与设计题

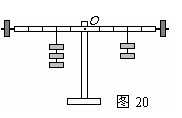
39．“研究杠杆的平衡条件”的实验如图20所示，回答下列问题：

①杠杆两端的调节螺母，是起调节杠杆_____　 的作用的。

②实验前先要调节杠杆两端的螺母，使其在水平位置平衡，这是为使杠杆所受的________通过支点，从而可以不考虑杠杆的重力对其转动的影响。

如果某同学做实验时发现杠杆左高右低，应将杠杆左端的螺母向________调；或将右端的螺

母向________调。

③调节好以后，仍要使杠杆在水平位置平衡，是为了__________。如杠杆不在水平位置平衡

时，应通过调节钩码的_______ 或_________来实现，而不能再调节________________。

④通过实验，得出的结论是：____________________________

40．“滑轮组的机械效率究竟与哪些因素有关”？某实验小组的同学对同一滑轮组进行实验

探究，得到了下表中的数据

①将表中数据补充完整。

②请在方框中画出进行第一次实验的装置图(每个钩码重2N).

③分析比较表中的数据，你认为同一滑轮组机械效率发生变化的主要原因是　　　　　　　　 　　。

次数 　 项目	1	2	3
钩码重／N	4	6	8
钩码上升高度/m	0.1	0.1	0.1
绳端拉力／N	1.8	2.4	3
绳端上移的距离／m	0.3	0.3	0.3
机械效率	74%	83%

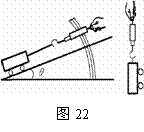
41．小刚同学设计了一个高度可调节的斜面来探究斜面的省力情况、斜面的机械效率与斜面的倾斜程度之间的关系，如图22所示。她首先测出小车重，然后用弹簧测力计沿斜面拉动小车，调节斜面倾斜角θ的大小多次测量，得到下表所示的数据：

(1)上表中的空格处①、②、③对应的数据分别是：__________、_________、___________。

(2)分析上表数据，得出的探究结论是：斜面倾斜角θ越_______(选填：大或小)，斜

面越______(选填：省力或费力)，斜面的机械效率越_______(选填：高或低)。

(3)实验过程中拉力的方向应与斜面__________。

⑷若想探究斜面的机械效率与物重的关系，则要保持_________________不变，斜面的光滑程度不变，只改变______________。

斜面 倾斜角θ	小车重G/N	斜面高 h/m	斜面长s/m	拉力 F/N	有用功 W有/J	总功 W总/J	机械效率η
12°	5	0.2	1	2.1	①	2.1	48%
30°	5	0.5	1	3.6	2.5	②	69%
45°	5	0.7	1	4.3	3.5	4.3	③

42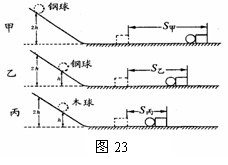．如图23所示，是用来研究"动能大小跟哪些因素有关"的实验装置图。小球在光滑斜面上由静止开始下滑，到达底端的速度只与起点高度有关，起点越高，到达底端的速度越大，运动小球撞击停在平面上的木块后，木块运动距离越长，说明小球具有动能越大.

①分析比较实验甲与实验乙，可得出结论：　　 _　　　　　　　　　　　　　　　　　

②分析比较实验乙与实验丙，可得出结论：____　　　　　　　　　　　　　　 　　　　　。

(三)作图题

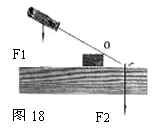
37．画出动力F1和阻力F2的力臂。

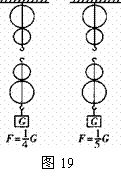
38．按照图的要求画出滑轮组的绕绳方法。(不计滑轮重、绳重及摩擦)