31.(2008天津)有4张分别标有数字1，2，3，4的红色卡片和4张分别标有数字1，2，3，4的蓝色卡片，从这8张卡片中取出4张卡片排成一行．如果取出的4张卡片所标数字之和等于10，则不同的排法共有________________种(用数字作答)．

答案432

30.(2008重庆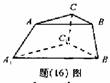)某人有4种颜色的灯泡(每种颜色的灯泡足够多)，要在如题(16)图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡，要求同一条线段两端的灯泡不同色，则每种颜色的灯泡都至少用一个的安装方法共有　　　　 种(用数字作答).

答案216

29.(2008陕西)某地奥运火炬接力传递路线共分6段，传递活动分别由6名火炬手完成．如果第一棒火炬手只能从甲、乙、丙三人中产生，最后一棒火炬手只能从甲、乙两人中产生，则不同的传递方案共有　　　　 种．(用数字作答)．

答案96

28．(2006重庆)高三(一)班学要安排毕业晚会的4各音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是

(A)1800　　 　　(B)3600　　 　　　　(C)4320　　 　　　　(D)5040

答案B

解：不同排法的种数为＝3600，故选B

27．(2006重庆)将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有

(A)30种　　(B)90种　　　　 (C)180种　　(D)270种

答案B

解析：将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则将5名教师分成三组，一组1人，另两组都是2人，有种方法，再将3组分到3个班，共有种不同的分配方案，选B.

26．(2006天津)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有(　)

A．10种　　　B．20种　　　C．36种 　　　D．52种

答案A

解析：将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，分情况讨论：①1号盒子中放1个球，其余3个放入2号盒子，有种方法；②1号盒子中放2个球，其余2个放入2号盒子，有种方法；则不同的放球方法有10种，选A．

25．(2006山东)已知集合A={5},B={1,2},C={1,3,4}，从这三个集合中各取一个元素构成空间直角坐标系中点的坐标，则确定的不同点的个数为

(A)33　　　　 (B) 34　　　　　 (C) 35　　　　　　　 (D)36

答案A

解析 ：不考虑限定条件确定的不同点的个数为＝36，但集合B、C中有相同元素1，由5，1，1三个数确定的不同点的个数只有三个，故所求的个数为36－3＝33个，选A

24．(2006全国II)5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有

　 (A)150种　 　　　　　　　　 (B)180种　 　　　　　 (C)200种　　 　　　　　　 　(D)280种

答案A　

解析：人数分配上有1,2,2与1,1,3两种方式，若是1,2,2，则有＝60种，若是1,1,3，则有＝90种，所以共有150种，选A

23．(2006全国I)设集合。选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有

A．　　　　 B．　　　　　　　 C．　　　　　　 D．

答案B

解析：若集合A、B中分别有一个元素，则选法种数有=10种；若集合A中有一个元素，集合B中有两个元素，则选法种数有=10种；若集合A中有一个元素，集合B中有三个元素，则选法种数有=5种；若集合A中有一个元素，集合B中有四个元素，则选法种数有=1种；若集合A中有两个元素，集合B中有一个元素，则选法种数有=10种；若集合A中有两个元素，集合B中有两个个元素，则选法种数有=5种；若集合A中有两个元素，集合B中有三个元素，则选法种数有=1种；若集合A中有三个元素，集合B中有一个元素，则选法种数有=5种；若集合A中有三个元素，集合B中有两个元素，则选法种数有=1种；若集合A中有四个元素，集合B中有一个元素，则选法种数有=1种；总计有，选B.

22．(2006湖南)在数字1,2，3与符号+，－五个元素的所有全排列中，任意两个数字都不相邻的全排列个数是

A．6　　　　　 　　B. 12 　　　　C. 18　　　　　　 D. 24

答案B

解析：先排列1，2，3，有种排法，再将“+”，“－”两个符号插入，有种方法，共有12种方法，选B.