
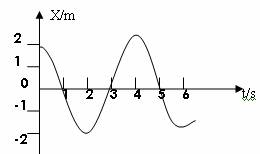
5.弹簧振子的周期是0.2秒,它在1秒内通过40cm的路程,它的振幅是多大?
解:
4.如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面,已知甲的质量大于乙的质量.当细线突然断开后,两物块都做简谐运动,在运动过程中(C).
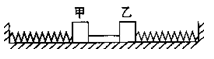

A.甲的振幅大于乙的振幅 B.甲的振幅小于乙的振幅
B.甲的振幅小于乙的振幅
C.甲的最大速度小于乙的最大速度 D.甲的最大速度大于乙的最大速度
D.甲的最大速度大于乙的最大速度
解:在细线未断之前,两个弹簧受的弹力是相等的,所以当细线断开后,甲、乙两物体做简谐运动的振幅是相等的,A、B均错;两物体在平衡位置时速度最大,此时的动能等于弹簧刚释放时的弹性势能,所以两物体的最大动能是相等的,则质量大的速度小,选C。
3.作简谐运动的物体,当它每次经过同一位置时,一定相同的物理量是( BCD )
(A)速度 (B)位移 (C)回复力 (D)加速度
.同一个弹簧振子从平衡位置被分别拉开5cm和2cm,松手后均作简谐运动,则它们的振幅之比A1:A2=5:2,最大加速度之比a1:a2=5:2,振动周期之比T1:T2=1:1
2.作简谐运动的物体每次通过平衡位置时( BC ).
(A)位移为零,动能为零 (B)动能最大,势能最小
(C)速率最大,振动加速度为零 (D)速率最大,回复力不一定为零
1.简谐运动属于下列运动中的( D ).
(A)匀速直线运动 (B)匀加速直线运动
(C)匀变速直线运动 (D)非匀变速直线运动
(提示:作简谐运动物体的同复力与位移的大小成正比、方向与其相反,故其加速度时刻变化)
6.振动过程中各物理量的变化情况
|
振动体位置 |
位移X |
回复力F |
加速度a |
速度v |
势能 |
动能 |
||||
|
方向 |
大小 |
方向 |
大小 |
方向 |
大小 |
方向 |
大小 |
|||
|
平衡位置O |
|
0 |
|
0 |
|
0 |
|
最大 |
最小 |
最大 |
|
最大位移处A |
指向A |
最大 |
指向O |
最大 |
指向O |
最大 |
|
0 |
最大 |
最小 |
|
平衡位置O→最大位移处A |
指向A |
0→最大 |
指向O |
0→最大 |
指向O |
0→最大 |
O→A |
最大→0 |
最小→最大 |
最大→最小 |
|
最大位移处A→平衡位置O |
指向A |
最大→0 |
指向O |
最大→0 |
指向O |
最大→0 |
A→O |
0→最大 |
最大→最小 |
最小→最大 |
说明:简谐运动的位移、回复力、加速度、速度都随时间做周期性变化(正弦函数),变化周期为T,振子的动能、势能也做周期性变化,周期为 T/2, 动能和势能之和不变。
① 凡离开平衡位置的过程,v、Ek均减小,x、F、a、EP均增大;
凡向平衡位置移动时,v、Ek均增大, x、F、a、EP均减小.
② 振子运动至平衡位置时,x、F、a为零,EP最小,v、Ek最大;
当在最大位移时,x、F、a、EP最大,v、Ek最为零;
③在平衡位置两侧的对称点上,x、F、a、v、Ek、EP的大小均相同.
5. 回复力:振动物体所受到的总是指向平衡位置的合外力
4.简谐运动的表达式
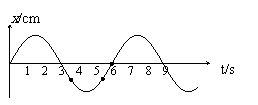 既然简谐运动的位移和时间的关系可以用正弦曲线或余弦曲线来表示,那么若以x代表质点对于平衡位置的位移,t代表时间,根据三角函数知识,x和t的函数关系可以写成 x=Asin(ωt+
既然简谐运动的位移和时间的关系可以用正弦曲线或余弦曲线来表示,那么若以x代表质点对于平衡位置的位移,t代表时间,根据三角函数知识,x和t的函数关系可以写成 x=Asin(ωt+ )
)
公式中的A代表振动的振幅,ω叫做圆频率,它与频率f之间的关系为:ω=2π/T=2πf;公式中的(ωt+ )表示简谐运动的相位,t=0时的相位
)表示简谐运动的相位,t=0时的相位 叫做初相位,简称初相。
叫做初相位,简称初相。
3.相位:相位是表示物体振动步调的物理量,用相位来描述简谐运动在一个全振动中所处的不同状态。
2. 周期和频率:
全振动:是指从某一初始时刻起,物体的振动状态再次恢复到初始时刻的过程。
①周期:做简谐运动的物体完成一次全振动所需的时间,叫做振动的周期。用T来表示,单位是秒(s)
②频率:单位时间内完成的全振动的次数,叫频率。用f来表示,单位是赫兹(Hz)。
③周期和频率之间的关系:T= =2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com