
18.解:(Ⅰ)
 . ………………… 3 分
. ………………… 3 分
当 时,
时, ,
, ,
,
所以曲线 在点
在点 处的切线方程为
处的切线方程为 ,
,
即 .
………………… 5 分
.
………………… 5 分
(Ⅱ)令 ,解得
,解得 或
或 .
.
①  ,则当
,则当 时,
时, ,函数
,函数 在
在 上单调递减,
上单调递减,
所以,当 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为 . ………………… 7分
. ………………… 7分
②  ,则当
,则当 时,
时,
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
极小值 |
 |
 |
所以,当 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为 . ………………… 10 分
. ………………… 10 分
③  ,则当
,则当 时,
时, ,函数
,函数 在
在 上单调递增,
上单调递增,
所以,当 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为 . ………… 12 分
. ………… 12 分
综上,当 时,
时, 的最小值为
的最小值为 ;当
;当 时,
时, 的最小值为
的最小值为 ;
;
当 时,
时, 的最小值为
的最小值为 .
………………… 13 分
.
………………… 13 分
17.解:(Ⅰ)设该同学在一次投掷中投中A区域的概率为 ,
,
依题意, .
………………… 3 分
.
………………… 3 分
(Ⅱ)依题意知,  ,从而
,从而 的分布列为:
的分布列为:










………………… 8 分
(Ⅲ)设 表示事件“第
表示事件“第 次击中目标时,击中
次击中目标时,击中 区域”,
区域”, 表示事件“第
表示事件“第 次击中目标时,击中
次击中目标时,击中 区域”,
区域”, .
.
依题意知 . ………………… 13 分
. ………………… 13 分
16.解法一:
(Ⅰ)证明:因为
 平面
平面 ,
,
所以 是
是 在平面
在平面 内的射影,
………………… 2 分
内的射影,
………………… 2 分
由条件可知

 ,
,
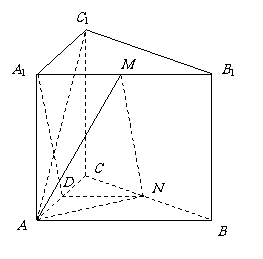 所以
所以 . ………………… 4 分
. ………………… 4 分
(Ⅱ)证明:设  的中点为
的中点为 ,
,
连接 ,
, .
.
因为 ,
, 分别是
分别是 ,
, 的中点,
的中点,
所以


 .
.
又 =
=
 ,
,

 ,
,
所以

 .
.
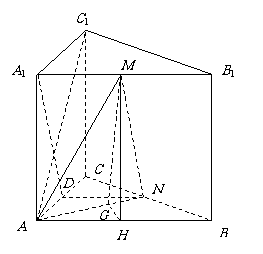 所以四边形
所以四边形 是平行四边形.
是平行四边形.
所以

 . ………………… 7 分
. ………………… 7 分
因为
 平面
平面 ,
,
 平面
平面 ,
,
所以 平面
平面 . …………… 9 分
. …………… 9 分
(Ⅲ)如图,设 的中点为
的中点为 ,连接
,连接 ,
,
所以

 .
.
因为
 底面
底面 ,
,
所以
 底面
底面 .
.
在平面 内,过点
内,过点 做
做

 ,垂足为
,垂足为 .
.
连接 ,则
,则

 .
.
所以
 是二面角
是二面角 的平面角.
………………… 12 分
的平面角.
………………… 12 分
因为 =
= =2,
=2,
由 ∽
∽ ,得
,得 =
= .
.
所以 =
= =
= .
.
所以 =
= =
= .
.
二面角 的余弦值是
的余弦值是 .
………………… 14 分
.
………………… 14 分
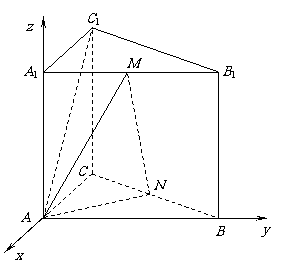 解法二:
解法二:
依条件可知 ,
, ,
, 两两垂直.
两两垂直.
如图,以点 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.
根据条件容易求出如下各点坐标:
 ,
, ,
, ,
,
 ,
, ,
, ,
,
 ,
, .
.
(Ⅰ)证明:因为 ,
, ,
,
所以
 .
………………… 2 分
.
………………… 2 分
所以 .
.
即 .
………………… 4 分
.
………………… 4 分
(Ⅱ)证明:因为 ,
, 是平面
是平面 的一个法向量,
的一个法向量,
且
 ,所以
,所以 .
………………… 7 分
.
………………… 7 分
又
 平面
平面 ,
,
所以 平面
平面 .
………………… 9 分
.
………………… 9 分
(Ⅲ)设 是平面
是平面 的法向量,
的法向量,
因为 ,
, ,
,
由 得
得 解得平面
解得平面 的一个法向量
的一个法向量 .
.
由已知,平面 的一个法向量为
的一个法向量为 .
………………… 12 分
.
………………… 12 分
设二面角 的大小为
的大小为 , 则
, 则 =
= =
= .
.
二面角 的余弦值是
的余弦值是 .
………………… 14 分
.
………………… 14 分
15.解:(Ⅰ) ………………… 2分
………………… 2分
 ………………… 4分
………………… 4分
 ………………… 6分
………………… 6分
故 的最小正周期为
的最小正周期为 .
………………… 7分
.
………………… 7分
(Ⅱ)
 ………………… 9 分
………………… 9 分

 …………………11分
…………………11分
因为
 ,
,
所以函数 是偶函数. …………………13分
是偶函数. …………………13分
9.
 10.
10. 11.
11. 12.
12. 13.
13.  14.② ③
14.② ③
注:14题少解给2分,有错解不给分.
1.B 2.C 3.B 4.A 5.A 6.B 7.D 8.B
20.(本小题满分14分)
数列 满足:
满足: ,
, .
.
(Ⅰ)若数列 为常数列,求
为常数列,求 的值;
的值;
(Ⅱ)若 ,求证:
,求证: ;
;
(Ⅲ)在(Ⅱ)的条件下,求证:数列 单调递减.
单调递减.
数学 (理科)评分参考
19.(本小题满分13分)
已知两点 ,
, ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 交于另一点
交于另一点 .
.
(Ⅰ)求曲线 的方程及离心率;
的方程及离心率;
(Ⅱ)设 ,若
,若
 ,求直线
,求直线 的方程.
的方程.
18.(本小题满分13分)
设 ,函数
,函数 .
.
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在
在 上的最小值.
上的最小值.
17.(本小题满分13分)
 如图,一圆形靶分成A,B,C三部分,其面积之比为
如图,一圆形靶分成A,B,C三部分,其面积之比为
 .某同学向该靶投掷
.某同学向该靶投掷 枚飞镖,每次1枚.假设他每
枚飞镖,每次1枚.假设他每
次投掷必定会中靶,且投中靶内各点是随机的.
(Ⅰ)求该同学在一次投掷中投中A区域的概率;
(Ⅱ)设X表示该同学在3次投掷中投中A区域的次数,求
X的分布列;
(Ⅲ)若该同学投中A,B,C三个区域分别可得3分,2分,
1分,求他投掷3次恰好得4分的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com