21、(本题满分14分)已知数列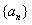中，是它的前项和，且

(1)证明为等比数列；

(2)设，求的通项公式；

(3)求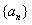的前项和

20、(本题满分13分)某商场以100元/件的价格购进一批衬衣，以高于进价的价格出售，销售有淡季和旺季之分，通过市场调查发现：

①销售量(件)与衬衣标价(元/件)在销售旺季近似地符合函数关系：；在销售淡季近似地符合函数关系：，其中，且为常数；

②在销售旺季，商场以140元/件的价格销售能获得最大销售利润；

③若称①中时的标价为衬衣的“临界价格”，则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍。

请根据上述信息，完成下面问题：

(1)填出表格中空格的内容；

数量关系 　 销售季节	标价(元/件)	销售量(件)(含或)	不同季节的销售总利润(元)与标价(元/件)的函数关系式
旺季
淡季

(2)在销售淡季，该商场要获得最大销售利润，衬衣的标价应定为多少元才合适？

19、(本题满分12分)已知函数

(1)求函数的最小正周期，对称轴方程；

(2)求函数的单调增区间；

(3)求在上的最小值和最大值。

18、(本题满分12分)已知二次函数满足，且关于的方程的两个实数根分别在区间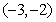和内，

(1)求实数的取值范围；

(2)若的解集为，求实数的值。

17、(本题满分12分)已知数列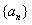的前项和，

(1)求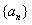的通项公式；

(2)设，求证：

16、(本题满分12分)已知函数，且

(1)求的值；

(2)若，且，求的值。

15、设函数的图像为，有下列四个命题：

①图像关于直线对称；

②图像的一个对称中心是；

③函数在区间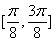上是增函数；

④图像可由的图像向左平移个单位得到；

其中真命题的序号是________________

14、某资料室在计算机使用中，如下表所示以一定规则排列的编码，且从左至右以及从上到下都是无限的。此表中主对角线上数列1，2，5，10，17，……的通项公式为________________，编码100共出现_______________次。

13、若奇函数在其定义域上是减函数，且对任意的，不等式恒成立，则的最大值是________________

12、设等比数列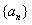的前项和为，且，则________________