
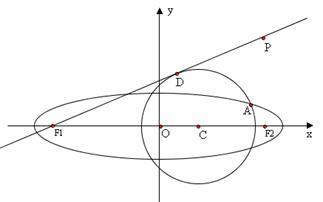
20.(本小题14分)已知点P(4,4),圆C: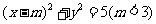 与椭圆E:
与椭圆E: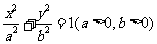 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线 与圆C相切.
与圆C相切.
 (1)求
(1)求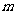 的值与椭圆E的方程;
的值与椭圆E的方程;
(2)设D为直线PF1与圆C 的切点,在椭圆E上是否存在点Q ,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。
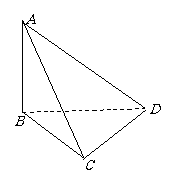
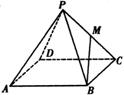
19.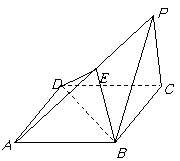 (本小题13分)已知PC⊥平面ABCD,四边形ABCD是菱形,边长为a,∠ABC=120°,且PC=a, E为PA的中点.
(本小题13分)已知PC⊥平面ABCD,四边形ABCD是菱形,边长为a,∠ABC=120°,且PC=a, E为PA的中点.
(1)求证:平面EBD⊥平面ABCD;
(2)求点E到平面PBC的距离;
(3)求二面角A-BE-D的大小.
18.(本小题12分) 一炮弹在A处的东偏北60°的某处爆炸,在A处测到爆炸信号的时间比在B处早4秒,已知A在B的正东方、相距6千米, P为爆炸地点(该信号的传播速度为每秒1千米),求A、P两地的距离.
17.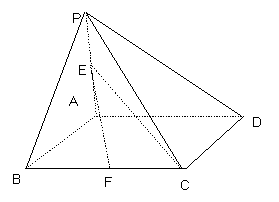 (本题满分12分)如图,四边形
(本题满分12分)如图,四边形 是正方形,
是正方形,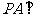 平面
平面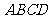 ,
,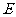 是
是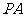 上的一点,
上的一点,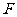 是
是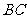 的中点
的中点
(1)求证: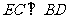 ;
;
(2)若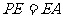 ,求证:
,求证: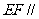 平面
平面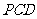 .
.
16. (本题满分10分)如图,
(本题满分10分)如图,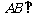 平面
平面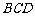 ,
,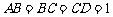 ,
,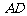 与平面
与平面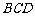 成
成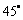 的角.求直线
的角.求直线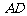 与平面
与平面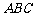 所成的角的大小(用反三角表示);
所成的角的大小(用反三角表示);
15.如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=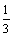 AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在平面直角坐标系
AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在平面直角坐标系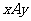 中,动点P的轨迹方程是
.
中,动点P的轨迹方程是
.
14.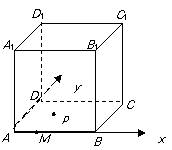 已知抛物线
已知抛物线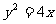 的准线与双曲线
的准线与双曲线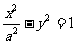 交于
交于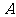 、
、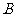 两点,点
两点,点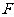 为抛物线的焦点,若
为抛物线的焦点,若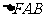 为直角三角形,则双曲线的离心率是
.
为直角三角形,则双曲线的离心率是
.
13.已知四边形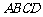 为正方形,P为面ABCD外一点,且
为正方形,P为面ABCD外一点,且
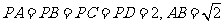 ,M是侧棱PC的中
,M是侧棱PC的中
点,则异面直线PA与BM所成角的大小为_________.
12. 曲线
曲线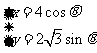 (
(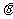 为参数)上一点
为参数)上一点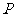 到点
到点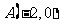 、
、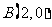 距离之和为________________。
距离之和为________________。
11.空间四边形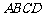 中,
中,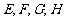 分别是
分别是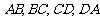 的中点,若
的中点,若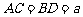 ,且
,且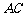 与
与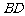 所成的角为
所成的角为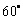 ,则四边形
,则四边形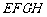 的面积是_______________;
的面积是_______________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com