
3、平衡位置:是振动物体受回复力等于零的位置;也是振动停止后,振动物体所在位置;平衡位置通常在振动轨迹的中点。“平衡位置”不等于“平衡状态”。平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态)
2、回复力:振动物体所受到的总是指向平衡位置的合外力.
①回复力时刻指向平衡位置;②回复力是按效果命名的, 可由任意性质的力提供.可以是几个力的合力也可以是一个力的分力; ③合外力:指振动方向上的合外力,而不一定是物体受到的合外力.④在平衡位置处:回复力为零,而物体所受合外力不一定为零.如单摆运动,当小球在最低点处,回复力为零,而物体所受的合外力不为零.
1、机械振动:物体(或物体的一部分)在某一中心位置两侧做的往复运动.
振动的特点:①存在某一中心位置;②往复运动,这是判断物体运动是否是机械振动的条件.
产生振动的条件:①振动物体受到回复力作用;②阻尼足够小;
5.根据以上的关系式,求得某一物理量
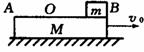
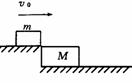 [例2]如图所示,质量为m的小铁块以初速度v0滑上质量为M,静止在光滑水平面上的木块,铁块与木块间的摩擦因数为μ,当M向右运动s时,m与M相对静止,m相对M滑动距离为Δs,则木块动能的增量,铁块动能的减少量,系统机械能的减少量,转化成内能的能量各是多少?
[例2]如图所示,质量为m的小铁块以初速度v0滑上质量为M,静止在光滑水平面上的木块,铁块与木块间的摩擦因数为μ,当M向右运动s时,m与M相对静止,m相对M滑动距离为Δs,则木块动能的增量,铁块动能的减少量,系统机械能的减少量,转化成内能的能量各是多少?
解析:对m与M在水平方向所受合外力为零,因而动量守恒
根据动量守恒定律m v0=(M+m)v……①
根据动能定理,对M ½Mv2=μmgs
对m: ½m v02一½mv2=μmg(s+Δs)
木块动能增量为μmgs=½M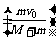 2
2
铁块动能减少量为:μmg(s+Δs)=½m v02-½m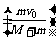 2
2
系统机械能的减少量为:½m v02一½mv2-½Mv2=μmgΔs
转化成内能的能量为:μmgΔs
答案: ½M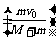 2,½m v02-½m
2,½m v02-½m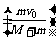 2,μmgΔs,μmgΔs
2,μmgΔs,μmgΔs
点评:从以上可知,(1)m动能减少量,转化成M的动能与系统的内能.
(2)系统机械能的减少量等于产生的内能
(3)从该题中也可以进一步认识到作用力、反作用力有时做功不同.
[例3]上题中ΔS与S比较,可能( )
A.一定ΔS<s; B.一定ΔS=S; C.一定ΔS>S;
D.以上结论均可能,但不能说是一定
解析:由m v0=(M+m)v得v=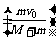 ,μmgs=½M
,μmgs=½M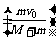 2
2
μmgΔs=½m v02一½mv2-½Mv2=½mv02一½m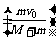 2-½M
2-½M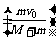 2
2
我们比较S与ΔS的大小,只要看μmgΔs一μmgs大于零或小于零,或者等于零即可.
μmgΔs一μmgs=½m v02一½m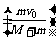 2-½M
2-½M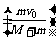 2-½M
2-½M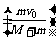 2=½m v02[1-
2=½m v02[1-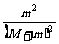 -
-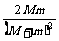 ]
]
对[1-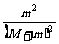 -
-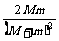 ]=
]=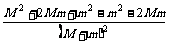 =
=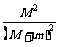 显然大于零
显然大于零
由以上讨论可知ΔS>S 答案:c
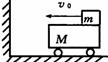 [例4]如图所示,质量M=lkg的平板小车右端放有质量m=2kge的物块(可视为质点),物块与车之间的动摩擦因数μ=0.5.开始时二者一起以v0=6m/s的速度向左端的光滑水平面上运动,并使车与墙发生正碰,没碰撞时间极短,且碰后车的速率与碰前的相同,车身足够长,使物块不能与墙相碰(g=10 rn/s2)求:
[例4]如图所示,质量M=lkg的平板小车右端放有质量m=2kge的物块(可视为质点),物块与车之间的动摩擦因数μ=0.5.开始时二者一起以v0=6m/s的速度向左端的光滑水平面上运动,并使车与墙发生正碰,没碰撞时间极短,且碰后车的速率与碰前的相同,车身足够长,使物块不能与墙相碰(g=10 rn/s2)求:
(1)物块相对于小车的总位移S是多少?
(2)小车与墙第一次相碰后小车所走的总路程SM为多少?
解析:(1)由于 m>M,两者以共同速度与墙相碰后,物块的动量大小比车的动量大,由于滑动摩擦力的作用,两者必会又以共同速度再次与墙相碰,如此反复直到两者一起停止在墙角边为止,设物体相对于车的位移为S,由能量转化和守恒定律得: μmgs=½(m+M)v02,所以s=(m+M)v02/2μmg=5.4m
(2)设v1=v0,车与墙第n次碰后边率为vn,则第(n+1)次碰后速率为vn+1,对物块与车由动量守恒得:
mvn-Mvn=(m+M)vn+1 所以vn+1=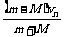 =
=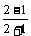 vn= vn/3.
vn= vn/3.
车与墙第(n+1)次碰后最大位移 sn+1=
vn+12/2a=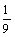
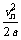 =Sn/9
=Sn/9
可见车每次与墙碰后的最大位移是一个等比数列,其q=1/9,所以车与墙碰后的总路程
SM=2(S1+S2+…+Sn+…)=2 S1·(1十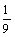 十…+
十…+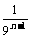 +…)=
+…)=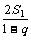
车第一次与墙碰后最大位移 S1=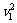 /2a=
/2a=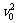 /2a,a=μmg/M=10m/s2
/2a,a=μmg/M=10m/s2
可算得 S1=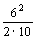 m=1.8 m 所以SM=
m=1.8 m 所以SM=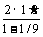 m=4.05n
m=4.05n
答案:(1)5.4 m(2)4.05 m
 点评:运用动量观点和动能观点解题每年在高考中都有很重的份量,每年的压轴题都是利用此观点解题.它们的特点是过程复杂、难度大、综合性强、灵活性高,这就要求我们主动去分析研究这类题的特点及处理所用的数学方法;在提高审题能力和物理过程分析能力上很下功夫,适度配合强化训练.
点评:运用动量观点和动能观点解题每年在高考中都有很重的份量,每年的压轴题都是利用此观点解题.它们的特点是过程复杂、难度大、综合性强、灵活性高,这就要求我们主动去分析研究这类题的特点及处理所用的数学方法;在提高审题能力和物理过程分析能力上很下功夫,适度配合强化训练.
[例5]如图所示,质量为M长为L的木板(端点为A、B,中点为O)置于光滑水平面上,现使木板M以v0的水平初速度向右运动,同时把质量为m长度可忽略的小木块置于B端(它对地初速为零),它与木板间的动摩擦因数为μ,问v0在什么范围内才能使小木块m滑动到OA之间停下来(即相对木板静止)?
解析:当 m、M相对静止时, m滑动到OA之间停下来的条件为:m相对M的位移s.½L≤s≤L.
由动量守恒M v0=(M十m)v
物体克服摩擦阻力相对位移的功,量度系统机械能的减少,所以 μmgs=½M v02-½(M+m)v2
解方程得s=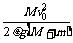 代入条件
代入条件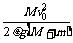 ≥½L所以v0≥
≥½L所以v0≥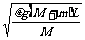
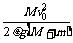 ≤L所以v0≤
≤L所以v0≤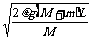
即:使m在OA间停下,v0满足的条件: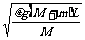 ≤v0≤
≤v0≤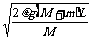
[例6]:A、B两球在光滑水平面上同向运动,A球动量PA=5kg·M/S,B球的动量为PB=7kg·m/s。A从后面追上B并发生碰撞,碰后B球的动量变为PB/=10kg·m/s,则两球质量mA与mB间的关系可能是:
A、 mB=mA; B、mB=2mA;C、mB=4mA; D、mB=6mA;
解:由动量守恒得PA+PB= PA/+PB/代入数据得PA/=2kg·m/s
由碰撞中动能不增特征知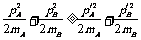 数据得mB≥2.5mA,由合理情景知在碰撞前速度应满足关系PA/mA>PB/mB可得mB>1.4mA
数据得mB≥2.5mA,由合理情景知在碰撞前速度应满足关系PA/mA>PB/mB可得mB>1.4mA
碰撞后速度应满足关系PA//mA≤PB//mB可得mB=5mA
综合得答案:C
[例7]如图所示,质量为M的天车静止在光滑水平轨道上,下面用长为L的细线悬挂着质量为m的沙箱,一颗质量为m0的子弹以v0的水平速度射入沙箱,并留在其中,在以后运动过程中
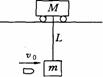 求:(1)沙箱上升的最大高度.
求:(1)沙箱上升的最大高度.
(2)天车的最大速度,
解析:(1)子弹打入沙箱过程中动量守恒m0v0=(m0+m)v1……①
摆动过程中,子弹、沙箱、天车系统水平方向动量守恒,机械能守恒。
沙箱到达最大高度时,系统有相同的速度,设为v2,则有
(m0+m)v1=(m0+m+M)v2……②
½(m0+m)v12=½(m0+m+M)v22+(m0+m)gh……③
联立①②③可得沙箱上升的最大高度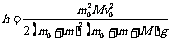
(2)子弹和沙箱再摆回最低点时,天车速度最大,设此时天车速度为v3,沙箱速度为v4,由动量守恒得
(m0+m)v1=Mv3+(m+M)v4……④
由系统机械能守恒得½(m0+m)v12=½Mv32+½(m+M)v42……⑤
联立④⑤求得天车的最大速度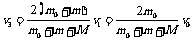
说明:(1)该题过程复杂,在子弹打沙箱的过程中动量守恒,机械能不守恒.共同摆动过程中,子弹、沙
箱、天车组成的系统水平方向动量守恒,系统机械能守恒.②式可列为m0v0=(m0+m+M)v2,但③式就不能列为½m0v02=½(m0+m+M)v22+(m0+m)gh,因子弹与沙箱打击过程中有机械能损失,这点是易错点,一定要分析清楚.
(2)④、⑤两个方程列出后,显然能看出与弹性碰撞方程相同,故解可直接写出,会节省很多时间,由此也可看出这一碰撞模型的重要性.
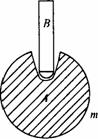 [例8]如图示是一个物理演示实验,它显示图中自由落体的物体A和B经反弹后,B能上升到比初始位置高得多的地方.
[例8]如图示是一个物理演示实验,它显示图中自由落体的物体A和B经反弹后,B能上升到比初始位置高得多的地方.
A是某种材料做成的实心球,质量m1=0. 28 kg,在其顶部的凹的坑中插着质量m2=0. 10 kg的木棍B,B只是松松地插在凹坑中,其下端与坑底之间有小空隙.将此装置从A下端离地板的高度H=1. 25 m处由静止释放.实验中,A触地后在极短时间内反弹,且速度大小不变;接着木棍B脱离球A开始上升,而球A恰好停留在地板上,求木棍B上升的高度,重力加速度g=10 m/s2.
解析:实心球A和木棍开始做自由落体运动,设它们就要落地的瞬间速度为v1,由运动学公式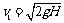
由题意,A触地后在极短的时间内反弹,速度变为向上,大小不变,仍为v1,而木棍由于松松地插在凹坑中,其下端与坑底间有空隙,受到的作用力的冲量可忽略,可认为速度大小,方向不变.由于A的速度变为向上,B的速度仍向下,A,B相向运动,之间接着产生很强的作用力,A对B作用力的冲量使B的速度方向变为向上,设大小为v2/, 而B对A的冲量使A的速度由v1减为零,恰好停留在地板上,这一过程属于碰撞模型,可认为在竖直方向A,B系统的动量守恒,取向上为正,由动量守恒定律得:
m1v1-m2v2=m2v2/(v1=v2)
以后,B脱离A以初速度v2/做竖直上抛运动,设木棍B上升的最大高度为h,由机械能守恒定律得:
½m2v2/2=m2gh,由以上几式联立,解得:h=4. 05 m
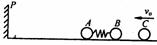 [例8]两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态。在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示。C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变,然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连。过一段时间,突然解除锁定(锁定及解除锁定无机械能损失)。已知A、B、C三球的质量均为m。
[例8]两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态。在它们左边有一垂直于轨道的固定挡板P,右边有一小球C沿轨道以速度v0射向B球,如图所示。C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变,然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不粘连。过一段时间,突然解除锁定(锁定及解除锁定无机械能损失)。已知A、B、C三球的质量均为m。
(1)求弹簧长度刚被锁定后A球的速度。
2)求在A球离开挡板P之后的运动过程中,弹簧的最大弹性势能。
解析(1)设C球与B球粘结成D时,D的速度为v1,由动量守恒,有mv0=(m+m)v1当弹簧压至最短时,D与A的速度相等,设此速度为v2,由动量守恒,有2mv1=3mv2。
由以上两式得A的速度v2=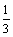 v0
v0
(2)设弹簧长度被锁定后,贮存在弹簧中的势能为EP,由能量守恒,有
½½×2mv12=½×3mv22+EP
撞击P后,A与D的动能都为零,解除锁定后,当弹簧刚恢复到自然长度时,势能全部转变成D的动能,设D的速度为v3,则有EP=½(2m)·v32
以后弹簧伸长,A球离开挡板P,并获得速度,当A、D的速度相等时,弹簧伸至最长,设此时的速度为v4,由动量守恒,有2mv3=3mv4
当弹簧伸到最长时,其势能最大,设此势能为EP/,由能量守恒,有
½½×2mv32=½×3mv42+EP/ 解以上各式得 E P/=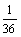 mv02
mv02
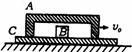 [例9]一段凹槽A倒扣在水平长木板C上,槽内有一小物块B,它到槽两内侧的距离均为L/2,如图所示,木板位于光滑水平的桌面上,槽与木板间的摩擦不计,小物块与木板间的摩擦因数为μ,A、B、C三者质量相等,原来都静止,现使槽A以大小为v0的初速度向右运动,已知v0<
[例9]一段凹槽A倒扣在水平长木板C上,槽内有一小物块B,它到槽两内侧的距离均为L/2,如图所示,木板位于光滑水平的桌面上,槽与木板间的摩擦不计,小物块与木板间的摩擦因数为μ,A、B、C三者质量相等,原来都静止,现使槽A以大小为v0的初速度向右运动,已知v0<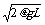 ,当A和B发生碰撞时,两者速度互换,求:
,当A和B发生碰撞时,两者速度互换,求:
(1)A与B刚发生第一次碰撞到第二次碰撞的时间内,木板内C运动的路程。
(2)在A、B刚要发生第四次碰撞时,A、B、C三者速度的大小。
解析:(1)A与B刚发生第一次碰撞后,A停下不动,B以初速度v0向右运动,由于摩擦,B向右作匀减速运动,而C向右作匀加速运动,两者速率渐接近,设B、C达到相同速度v1时B移动的路程为s1.设A、B、C质量皆为m,由动量守恒定律得mv0=2mv1
由功能转化得:μmgs1=½mv02-½mv12
联立上式得v1=½v0;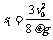
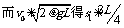
可见,在B、C达到相同速度v1时,B尚未与A发生第二次碰撞,B与C-起将以v1向右匀速运动一段距离(L-s1)后才与A发生第二次碰撞。设C的速度从零变到v1的过程中,C的路程为s2,由功能关系得μmgs2=½mv12得s2=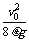 ,因此在第一次到第二次碰撞间C的路程为
,因此在第一次到第二次碰撞间C的路程为 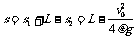
(2)由上面讨论可知,在刚要发生第二次碰撞时,A静止。B、C的速度均为v1,刚碰撞后,B静止,A、C的速度均为v1。由于摩擦,B将加速,C将减速,直至达到相同速度v2
由动量守恒定律得 mv1=2mv2 解得v2=½v1=¼v0
因A的速度v1大于B的速度v2,故第三次碰撞发生在A的左室,刚碰撞后,A的速度变为v2,B的速度变为v1,C的速度仍为v2,由于摩擦,B减速,C加速,直至达到相同速度v3,由动量守恒定律得mv1+mv2=2mv3 解得 v3=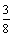 v0
v0
故刚要发生第四次碰撞时,A、B、C的速度分别为vA=v2=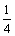 v0,vB=vC=v3=
v0,vB=vC=v3=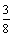 v0
v0
点评(1)考查了动量守恒定律与动能定理的综合应用,这是动量守恒定律与其他知识结合的常见形式。
(2)找准研究对象和研究过程,反复建立动量守恒方程,这是对考生综合素质的考查。
(3)题目新颖、灵活,考查了考生的推理能力。归纳能力、随机应变能力。
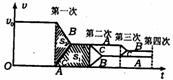 (4)此题区分度高,是压轴题,但可利用图家法巧解(如图所示).
(4)此题区分度高,是压轴题,但可利用图家法巧解(如图所示).
由题及图知sl+s2=L, sl=L一s2
又s2=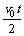 =
=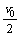
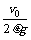 =
=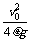
至于刚要发生第四次碰撞时,A、B、c三者速度由图一目了然。
[例10]一个连同装备总质量为M=100kg的宇航员,在距离飞船s=45m处与飞船处于相对静止,宇航员背着装有质量为m0=0.5kg氧气的贮气筒,筒有个可以使氧气以v=50m/s的速度喷出的喷嘴,宇航员必须向着返回飞船的相反方向放出氧气,才能回到飞船,同时又必须保留一部分氧气供途中呼吸用。宇航员的耗氧率为Q=2.5×10-4kg/s.不考虑喷出 氧气对设备及宇航员总质量的影响,则(1)瞬时喷出多少氧气,宇航员才能完全返回飞船;(2)为了使总耗氧量最低、应一次喷出多少氧气?返回时间又是多少?(3)已知超氧化钾(KO2)的性质与Na2O2相似,若该宇航员贮气筒的氧气由超氧化钾提供,则需用多少千克KO2?
解析(1)以飞船为参照物,向着飞船运动的方向为正方向,设喷出m(kg)氧气,宇航员获得的速度为V1,根据动量定恒定律,有: (M-m)V1-mv=0
考虑到M>>m,有V1=mv/M………①
宇航员返回飞船做匀速运动,历时: t=s/V1………②
又筒内氧气的总质量满足关系式: m0=Qt+m ………③
联立①②③并代入数据得 0.5=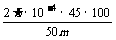 +m
+m
解之得 ml=0.05kg或 m2=0.45kg.故喷出的氧气 0.05kg<m<0.45kg·
(2)为了耗氧量最低,设喷出 m(kg)氧气则耗氧为 Δm=Qt+m……④
将①②代入④得Δm=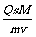 +m=
+m=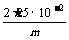 +m
+m
故当m=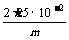 时,Δm有极小值。 即m=
时,Δm有极小值。 即m=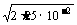 =0.15(kg),返回时间t=
=0.15(kg),返回时间t=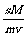 =600(s)
=600(s)
(3)由4KO2+2CO2=2K2CO3+3O2可知,284kg的KO2可制得96kg的O2,所以制取0.5kg的O2需KO2的质量为:0.5×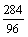 =1.48(kg).
=1.48(kg).

4.这当中有时要用到机械能守恒或能量守恒定律,可根据具体情况列出关系式.
3.对系统中的物体受力分析,找出外力总功与物体始末动能,从而应用动能定理列关系式.
2.对系统分析,看是否动量守恒(有时是某一方向动量守恒),再根据动量守恒定律列方程.
1.选出要研究的系统.
能量与动量结合的题目,过程复杂,知识综合性强,难度比较大;它不仅在力学中出现,在电学与原子核物理学中也都有类似的题目.因而在高考中那些难度大的题目往往出现在这里.
2.灵活应用动量、能量关系.有的题目可能动量守恒,机械能不守恒,或机械能守恒,动量不守恒,或者动量在整个变化过程中守恒,而机械能在某一个过程中有损失等,过程的选取要灵活,既要熟悉一定的典型题,又不能死套题型、公式.
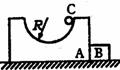 [例1]如图所示,A和B并排放在光滑的水平面上,A上有一光滑的半径为R的半圆轨道,半圆轨道右侧顶点有一小物体C,C由顶点自由滑下,设A、B、C的质量均为m.求:
[例1]如图所示,A和B并排放在光滑的水平面上,A上有一光滑的半径为R的半圆轨道,半圆轨道右侧顶点有一小物体C,C由顶点自由滑下,设A、B、C的质量均为m.求:
(1)A、B分离时B的速度多大?
(2)C由顶点滑下到沿轨道上升至最高点的过程中做的功是多少?
分析:小物体C自由滑下时,对槽有斜向右下方的作用力,使A、B一起向右做加速运动,当C滑至槽的最低点时,C、A之间的作用力沿竖直方向,这就是A、B分离的临界点,因C将沿槽上滑,C对A有斜向左下方的作用力,使A向右做减速运动,而B以A分离时的速度向右做匀速运动,C沿轨道上升到最大高度时,C与A的相对速度为零,而不是C对地的速度为零,至于C在全过程中所做的功,应等于A、B、C组成的系统动能的增加(实际上是等于C的重力所做的功)。
解析:对A、B、C组成的系统,它们在水平向上所受外力零,系统在水平方向上动量守恒,则 2mvAB+mvC=0 ………①
又系统内仅有重力弹力做功,机械能守恒,有mgR=½(2m)vAB2+½mvc2………②
联立①②解得vAB=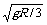 ,vC=-2
,vC=-2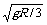 ,即分离时B的速度为
,即分离时B的速度为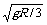 .
.
(2)当C上升到最高点时,C与A有共同速度vAB,对A、B、C系统,由动量守恒定律,mvAB+mvC=2mvAC
解之得vAC=-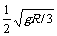 .
.
所以W=½mvAB2+½2mvc2=½m(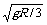 )2+½×2m(
)2+½×2m(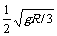 )2=
)2=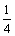 mgR.
mgR.
点评:本题把动量守恒定律和机械能守恒定律巧妙地结合一起,考查对物理过程分析和描述的能力,关键是能清晰地将整个物理过程划分两个阶段,应用于恒定律来解。
规律方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com