
8.已知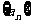 为等差数列,
为等差数列,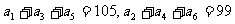 ,
,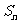 是等差数列
是等差数列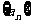 的前
的前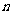 项和 ,则使得
项和 ,则使得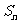 到达最大值的
到达最大值的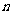 是 ( )
是 ( )
A. 21 B. 20 C. 19 D. 18
7. 已知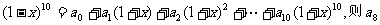 = ( )
= ( )
A.180 B.-180 C.45 D.-45
6.在 中,若
中,若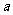 =1,C=
=1,C=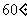 ,
, 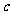 =
=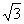 则A的值为 ( )
则A的值为 ( )
A.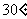 B.
B.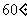 C.
C.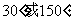 D.
D.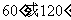
5.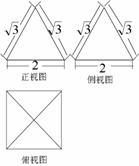 已知几何体的三视图(如右图),则该几何体的
已知几何体的三视图(如右图),则该几何体的
体积为 ( )
A.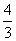 B.
B.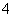
C.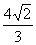 D.
D.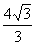
4.等差数列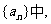
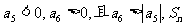 为数列
为数列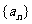 的前
的前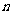 项和,则使
项和,则使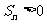 的
的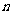 的最小值为 ( )
的最小值为 ( )
A.11 B.10 C.6 D.5
3. 给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一条直线和两个平行平面中的一个平面垂直,那么这条直线也和另一个平面垂直;
③若一条直线和两个互相垂直的平面中的一个平面垂直,那么这条直线一定平行于另一个平面;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是 ( )
A.①和② B.②和③ C.③和④ D.②和④
2.
在 中,如果
中,如果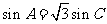 ,
,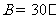 ,那么角
,那么角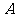 等于 ( )
等于 ( )
A.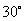 B.
B.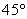 C.
C.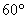 D.
D.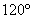
1.
“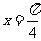 ”是“函数
”是“函数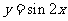 取得最大值”的
( )
取得最大值”的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12、已知函数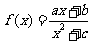 是定义在R上的奇函数,且当x=1时f(x)取最大值1.
是定义在R上的奇函数,且当x=1时f(x)取最大值1.
(1)求出a,b,c的值并写出f(x)的解析式;
(2)若x1∈(0,1),xn+1=f(xn),试比较xn+1与xn的大小并加以证明;
(3)若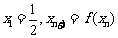 ,求证
,求证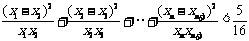 .
.
解:(1)∵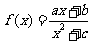 的定义域为R,∴c>0
的定义域为R,∴c>0
又∵f(x)为奇函数,∴f(-x)+f(x)=0,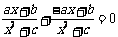 , b=0
,
, b=0
,
∴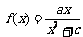 ,又f(1)=1,∴a=1+c>0,∴当x>0时,
,又f(1)=1,∴a=1+c>0,∴当x>0时,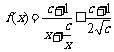
∴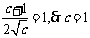 ∴a=2,b=0,c=1,
∴a=2,b=0,c=1,
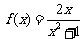
(2)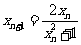 ,∵x1∈(0,1),∴xn+1>0(n∈N*)
,∵x1∈(0,1),∴xn+1>0(n∈N*)
又 矛盾,∴xn+1<1
矛盾,∴xn+1<1
∴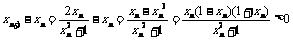 ∴xn+1>xn。
∴xn+1>xn。
(3)∵0<xk<1,
∴
∴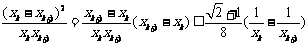

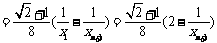
∵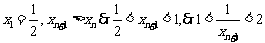
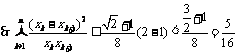
11、设数列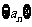 满足:
满足: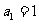 ,且当
,且当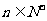 时,
时,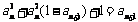
(1) 比较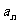 与
与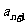 的大小,并证明你的结论;
的大小,并证明你的结论;
(2) 若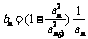 ,其中
,其中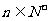 ,证明:
,证明: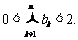
解:(1)由于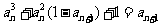 ,则
,则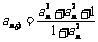 ,
,
∴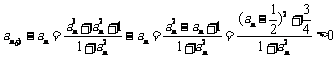 ,∴
,∴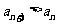
(2)由于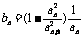 ,由(1)
,由(1)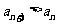 ,则
,则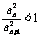 ,
,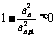 ,
,
而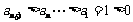 ,则
,则 ,∴
,∴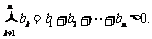
又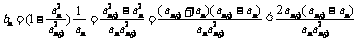
∴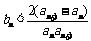 ,
,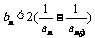
∴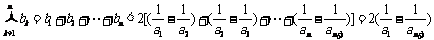 ,
,
而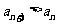 ,且
,且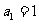 ,故
,故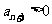
∴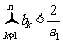 ,因此
,因此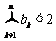 ,从而
,从而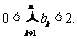
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com