
读“我国南、北方水资源、人口及耕地分布对照图(%)”,回答10~11题。
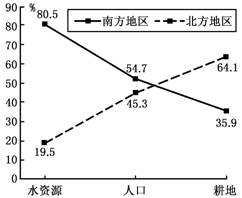
10.下列有关图中内容说法正确的是
A.我国人口重心在北方地区 B.南方的人均耕地面积不到北方的一半
C.人均耕地面积南方多于北方 D.南方的人均水资源为北方的4倍
11.造成我国南方和北方地区水资源总量差异大的主要原因是
A.雨季长短导致降水量差异较大 B.耕地面积差异较大
C.城市化水平差异较大 D.纬度差异导致蒸发量差异大
读地球公转到某位置时的示意图,图中虚线箭头代表地球公转轨道和方向,弧线MPN表示晨昏线,虚线圈表示回归线和极圈,最外圈表示赤道。回答7~9题。
7.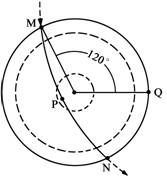 此时在M地某人观测太阳,太阳位于观测者的
此时在M地某人观测太阳,太阳位于观测者的
A.东北方
B.东南方
C.西北方
D.正西方
8.如果Q点所在经线两侧日期不同,则此时
A.地球公转速度较快
B.北京时间为8时
C.东京地方时为6:00
D.新的一天所占经度范围小于全球的二分之一
9.图示季节,下列现象可能发生的是
A.江淮地区农民忙于抗旱 B.希腊雅典阴雨连绵
C.开普敦附近海域的船员常感闷热异常 D.巴西高原草木茂盛
读黄河干支流部分河段水质状况分布图,判断4~6题。
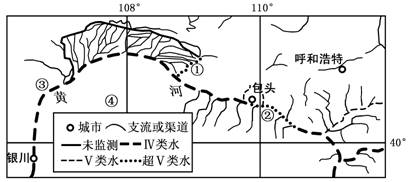
4.有关①、②两河段水质状况及成因分析正确的是
A.①河段水质较好,因为该河段流域内工业布局较少
B.①河段水质较差,主要由于该河段上游支流植被覆盖差,水土流失严重
C.②河段水质较好,因为该河段支流多,河流净化能力强
D.②河段水质较差,因为该河段工业污染大
5.从③河段到②河段,黄河干流
A.平均流量明显加大 B.地势逐渐降低
C.含沙量显著增大 D.结冰期逐渐变短
6.最适宜对乙地主要环境问题进行直接监测的现代地理信息技术是
A.地理信息系统 B.数字地球 C.遥感技术 D.全球定位技术
读我国某地区等高线地形图(单位:米),读图回答1~3题。
1.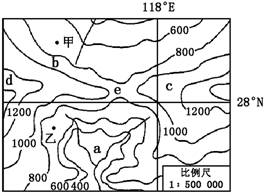 从影响农业的自然区位条件分析,村庄a、b、c、d中发展种植业最具有优势的是
从影响农业的自然区位条件分析,村庄a、b、c、d中发展种植业最具有优势的是
A.a村 B.b村 C.c村 D.d村
2.为发展经济,计划在村庄甲、乙之间修一条公路,最合理的走向是经过
A.b村 B.c村 C.d村 D.e村
3.图示区域最有特色的经济作物是
A.油菜、棉花 B. 茶叶、柑橘
C. 茶叶、甘蔗 D. 棉花、甜菜
9.(本小题满分14分)
已知数列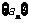 各项均不为0,其前
各项均不为0,其前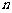 项和为
项和为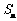 ,且对任意
,且对任意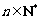 都有
都有 (
( 为大于1的常数),记
为大于1的常数),记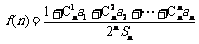 .
.
(1) 求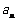 ;
;
(2) 试比较 与
与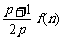 的大小(
的大小(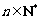 );
);
(3) 求证: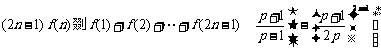 ,(
,( ).
).
解:(1) ∵ , ①
, ①
∴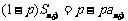 . ②
. ②
②-①,得
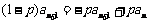 ,
,
即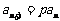 . (3分)
. (3分)
在①中令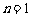 ,可得
,可得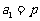 .
.
∴ 是首项为
是首项为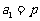 ,公比为
,公比为 的等比数列,
的等比数列,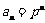 . (4分)
. (4分)
(2) 由(1)可得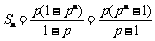 .
.
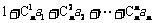
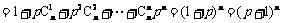 .
.
∴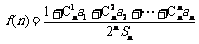
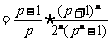 , (5分)
, (5分)

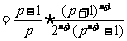 .
.
而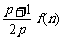
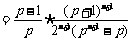 ,且
,且 ,
,
∴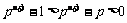 ,
,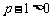 .
.
∴
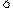
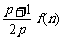 ,(
,(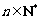 ). (8分)
). (8分)
(3) 由(2)知 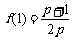 ,
,
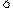
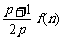 ,(
,(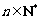 ).
).
∴当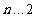 时,
时,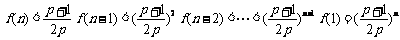 .
.
∴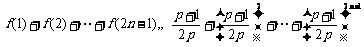
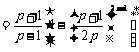 , (10分)
, (10分)
(当且仅当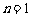 时取等号).
时取等号).
另一方面,当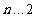 ,
,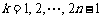 时,
时,
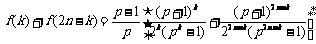
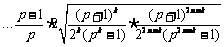
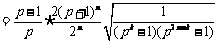
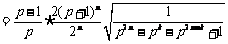 .
.
∵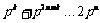 ,∴
,∴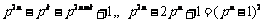 .
.
∴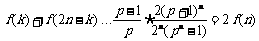 ,(当且仅当
,(当且仅当 时取等号).(13分)
时取等号).(13分)
∴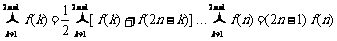 .(当且仅当
.(当且仅当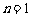 时取等号).
时取等号).
综上所述,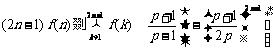 ,(
,(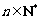 ).(14分)
).(14分)
8. (本小题满分12分)
(本小题满分12分)
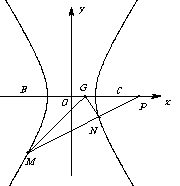
如图,直角坐标系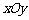 中,一直角三角形
中,一直角三角形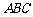 ,
,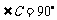 ,
,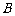 、
、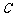 在
在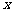 轴上且关于原点
轴上且关于原点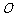 对称,
对称,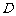 在边
在边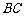 上,
上,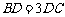 ,
,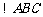 的周长为12.若一双曲线
的周长为12.若一双曲线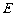 以
以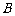 、
、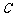 为焦点,且经过
为焦点,且经过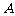 、
、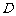 两点.
两点.
(1) 求双曲线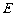 的方程;
的方程;
(2) 若一过点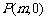 (
(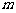 为非零常数)的直线
为非零常数)的直线 与双曲线
与双曲线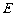 相交于不同于双曲线顶点的两点
相交于不同于双曲线顶点的两点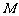 、
、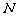 ,且
,且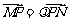 ,问在
,问在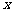 轴上是否存在定点
轴上是否存在定点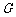 ,使
,使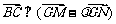 ?若存在,求出所有这样定点
?若存在,求出所有这样定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
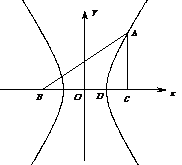 解:(1)
设双曲线
解:(1)
设双曲线 的方程为
的方程为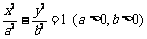 ,
,
则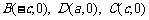 .
.
由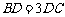 ,得
,得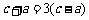 ,即
,即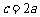 .
.
∴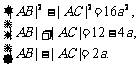 (3分)
(3分)
解之得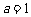 ,∴
,∴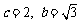 .
.
∴双曲线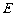 的方程为
的方程为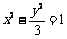 . (5分)
. (5分)
(2) 设在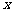 轴上存在定点
轴上存在定点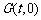 ,使
,使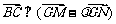 .
.
 设直线
设直线 的方程为
的方程为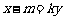 ,
,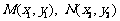 .
.
由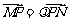 ,得
,得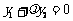 .
.
即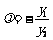 ① (6分)
① (6分)
∵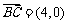 ,
,
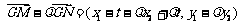 ,
,
∴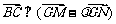
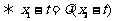 .
.
即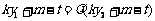 . ② (8分)
. ② (8分)
把①代入②,得
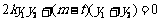 ③ (9分)
③ (9分)
把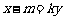 代入
代入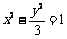 并整理得
并整理得
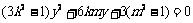
其中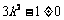 且
且 ,即
,即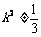 且
且 .
.
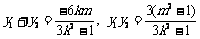 . (10分)
. (10分)
代入③,得
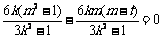 ,
,
化简得 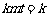 .
.
当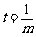 时,上式恒成立.
时,上式恒成立.
因此,在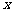 轴上存在定点
轴上存在定点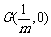 ,使
,使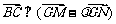 . (12分)
. (12分)
7.(本小题满分14分)
设函数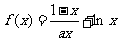 在
在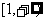 上是增函数.
上是增函数.
(1)
求正实数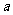 的取值范围;
的取值范围;
(2)
设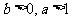 ,求证:
,求证: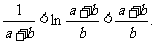
解:(1) 对
对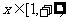 恒成立,
恒成立,
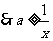 对
对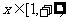 恒成立
恒成立
又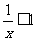
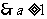 为所求.…………………………4分
为所求.…………………………4分
(2)取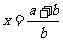 ,
,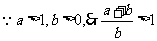 ,
,
一方面,由(1)知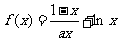 在
在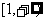 上是增函数,
上是增函数,
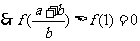
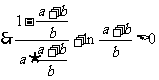
即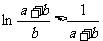 ……………………………………8分
……………………………………8分
另一方面,设函数
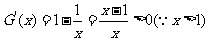
∴ 在
在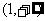 上是增函数且在
上是增函数且在 处连续,又
处连续,又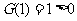
∴当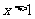 时,
时,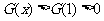
∴ 即
即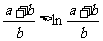
综上所述,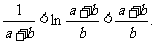 ………………………………………………14分
………………………………………………14分
又MN⊥MQ,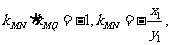 所以
所以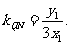
直线QN的方程为 ,又直线PT的方程为
,又直线PT的方程为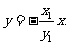 ……10分
……10分
从而得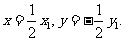 所以
所以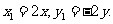
代入(1)可得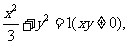 此即为所求的轨迹方程.………………13分
此即为所求的轨迹方程.………………13分
6.(本小题满分12分)
过抛物线 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,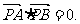
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数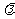 使得
使得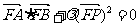 ?若存在,求出
?若存在,求出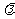 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
解法(一):(1)设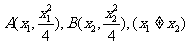
由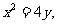 得:
得: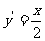
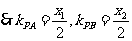
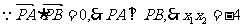 ………………………………3分
………………………………3分
直线PA的方程是: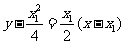 即
即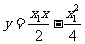 ①
①
同理,直线PB的方程是: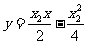 ②
②
由①②得: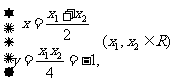
∴点P的轨迹方程是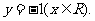 ……………………………………6分
……………………………………6分
(2)由(1)得: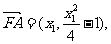
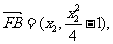
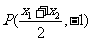

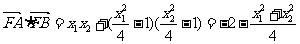 …………………………10分
…………………………10分
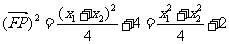
所以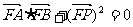
故存在 =1使得
=1使得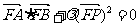 …………………………………………12分
…………………………………………12分
解法(二):(1)∵直线PA、PB与抛物线相切,且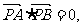
∴直线PA、PB的斜率均存在且不为0,且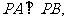
设PA的直线方程是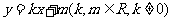
由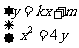 得:
得: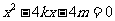
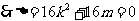 即
即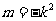 …………………………3分
…………………………3分
即直线PA的方程是:
同理可得直线PB的方程是: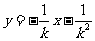
由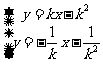 得:
得: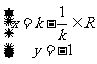
故点P的轨迹方程是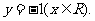 ……………………………………6分
……………………………………6分
(2)由(1)得: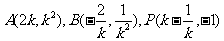
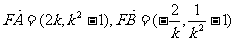

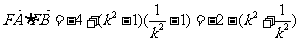 ………………………………10分
………………………………10分
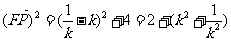
故存在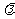 =1使得
=1使得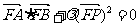 …………………………………………12分
…………………………………………12分
21. (本小题满分12分)
数列{an}中a1 = 2,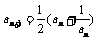 ,{bn}中
,{bn}中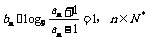 .
.
求证:数列{bn}为等比数列,并求出其通项公式;
当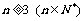 时,证明:
时,证明: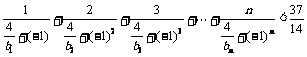 .
.
20. (本小题满分12分)
已知点A(– 2,0),B(2,0),动点P满足: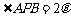 ,且
,且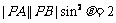 .
.
求动点P的轨迹G的方程;
过点B的直线l与轨迹G交于两点M、N.试问在x轴上是否存在定点C ,使得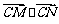 为常数.若存在,求出点C的坐标;若不存在,说明理由.
为常数.若存在,求出点C的坐标;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com