
22.(12分)解:(Ⅰ)设A、B两点的坐标分别为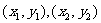
由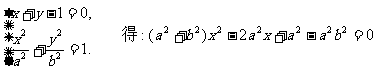 …………2分
…………2分
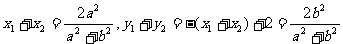 ,
,
∴点M的坐标为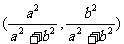 …………4分
…………4分
又点M的直线l上: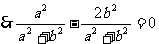

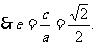 …………6分
…………6分
(Ⅱ)由(Ⅰ)知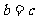 ,设椭圆右焦点
,设椭圆右焦点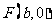 关于直线l:
关于直线l: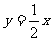 的对称点为
的对称点为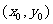 ,
,
由 …………8分
…………8分
解得:  …………10分
…………10分
∵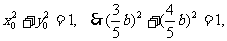
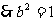 ,
,
∴所求的椭圆的方程为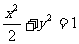 …………12分
…………12分
21.(12分)解:(Ⅰ)当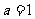 时,
时,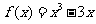 ,
,
所以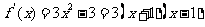 ,………2分
,………2分
令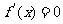 得:
得: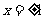 . ……3分
. ……3分
列表:
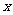 |
 |
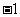 |
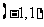 |
1 |
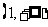 |
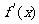 |
+ |
0 |
- |
0 |
+ |
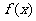 |
  |
极大值 |
  |
极小值 |
  |
∴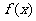 的单调递增区间是
的单调递增区间是 ,
,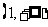 ;单调递减区间是
;单调递减区间是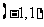 . ……5分
. ……5分
(Ⅱ)由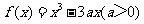 得
得
∵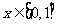
∴①当0<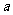 <1时,
<1时,
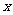 |
0 |
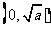 |
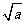 |
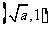 |
1 |
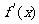 |
|
- |
0 |
+ |
|
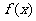 |
0 |
  |
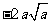 |
  |
 |
∴当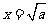 时,
时,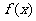 取得最小值,最小值为
取得最小值,最小值为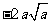 .
…………8分
.
…………8分
②当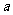 ≥1时
≥1时
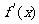 ≤0,
≤0,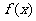 在
在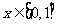 上是减函数,当
上是减函数,当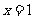 时,
时,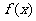 取得最小值,最小值为1-3
取得最小值,最小值为1-3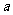 .
…………11分
.
…………11分
综上可得: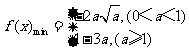 …………12分
…………12分
19. (12分)解:(Ⅰ)记“2次汇报活动都是由小组成员甲发言”为事件A则2次汇报活动都是由小组成员甲发言的概率为P(A) …………1分
由题意,得事件A的概率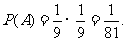 …………3分
…………3分
即2次汇报活动都是由小组成员甲发言的概率为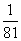 …………………………4分
…………………………4分
(Ⅱ)由题意,每次汇报时,男生被选为代表的概率为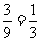 ,女生被选为代表的
,女生被选为代表的
概率为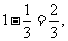 ………………………………………………6分
………………………………………………6分
记“男生发言次数不少于女生发言次数”为事件B,由题意,事件B包括以下两个互斥事件:
①事件B1:男生发言2次女生发言0次,其概率为:
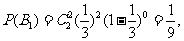 ………………………8分
………………………8分
②事件B2:男生发言1次,女生发言1次,其概率为:
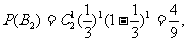 ………………………10分
………………………10分
因此男生发言次数不少于女生发言次数的概率为
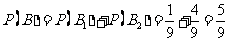 .
……………………… 12分
.
……………………… 12分
20(12分)解:
(Ⅰ)因为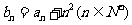 ,
,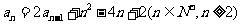 , 所以
, 所以
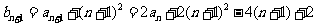
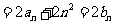 , …………4分
, …………4分
又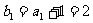 ,故
,故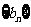 是以2为首项,公比为2的等比数列. ……………6分
是以2为首项,公比为2的等比数列. ……………6分
(Ⅱ)由(Ⅰ)得: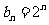 ,所以
,所以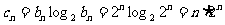 ,……8分
,……8分
从而
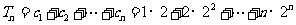 ,①
,①
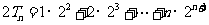 ②
②
①-②得:
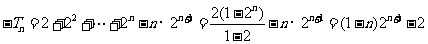 ……10分
……10分
所以,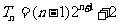 ………………………………………………12分
………………………………………………12分
18.(12分)(解法一)
解:(I)连结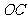 ,
,
 和
和 为等边三角形,
为等边三角形, 为
为 的中点,
的中点,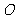 为
为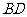 的中点,
的中点,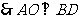 ,
,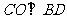 ,又
,又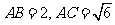 ,
,
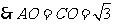 .…………2分
.…………2分
在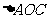 中,
中,
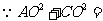
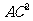 ,
,
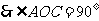 ,即
,即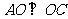
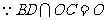 ,
,
∴ 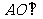 平面
平面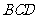 ………………………………………………4分
………………………………………………4分
(Ⅱ)过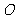 作
作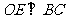 于
于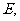 连结
连结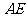 ,
,
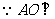 平面
平面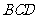 ,
,
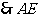 在平面
在平面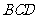 上的射影为
上的射影为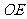
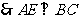
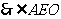 为二面角
为二面角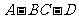 的平面角. ……………………6分
的平面角. ……………………6分
在 中,
中,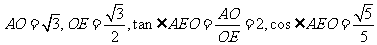
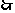 二面角
二面角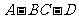 的余弦值为
的余弦值为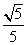 …………………………8分
…………………………8分
(Ⅲ)设点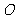 到平面
到平面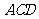 的距离为
的距离为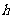
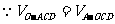 ,
,
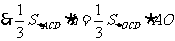 ……………………………10分
……………………………10分
在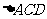 中,
中,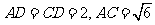 ,
,
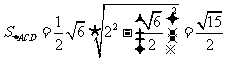
而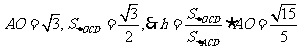
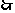 点
点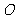 到平面
到平面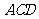 的距离为
的距离为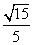 . ………………………12分
. ………………………12分
(解法二)
解:(I)同解法一…………………………………………………………4分
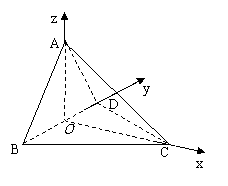 (Ⅱ)以
(Ⅱ)以 为原点,如图建立空间直角坐标系,
为原点,如图建立空间直角坐标系,
则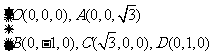
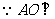 平面
平面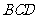 ,
,
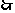 平面
平面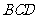 的法向量
的法向量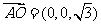 …………6分
…………6分
设平面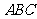 的法向量
的法向量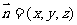
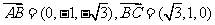
由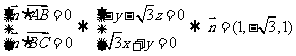
设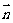 与
与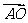 夹角为
夹角为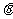 ,则
,则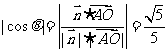
∴二面角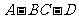 的余弦值为
的余弦值为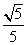 .……………………8分
.……………………8分
(Ⅲ)设平面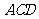 的法向量为
的法向量为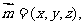 又
又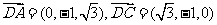
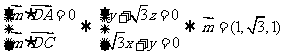 …………10分
…………10分
设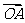 与
与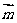 夹角为
夹角为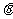 ,
,
则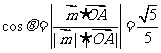
设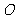 到平面
到平面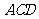 的距离为
的距离为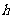 ,
,
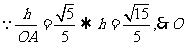 到平面
到平面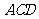 的距离为
的距离为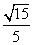 ……12分
……12分
17.(10分) 解:(Ⅰ)由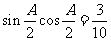 ,可得
,可得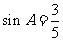 ,………1分
,………1分
因为A是锐角,所以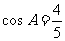 , …………………………………………3分
, …………………………………………3分

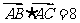 ,
, 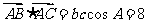 ,
,
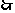
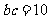 . ………………………………………………………………5分
. ………………………………………………………………5分
(Ⅱ)由余弦定理可得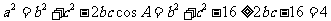 ,……8分
,……8分
当且仅当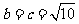 时取等号.所以
时取等号.所以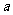 的最小值为2.
…………10分
的最小值为2.
…………10分
22. (本小题满分12分)
已知直线 相交于
相交于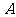 、
、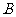 两点,线段
两点,线段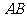 的中点
的中点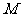 在直线
在直线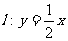 上.
上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆右焦点关于直线l的对称点在单位圆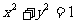 上,求椭圆的方程.
上,求椭圆的方程.
2010年邯郸市高三摸底考试文科数学答案及评分标准 2009.12.26
21. (本小题满分12分)
已知函数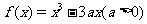 .
.
(Ⅰ)当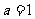 时,求
时,求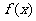 的单调区间;
的单调区间;
(Ⅱ)求函数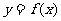 在
在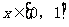 上的最小值.
上的最小值.
20. (本小题满分12分)
已知数列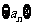 的首项
的首项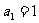 ,
, 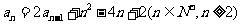
(Ⅰ)设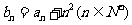 ,证明
,证明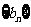 是等比数列;
是等比数列;
(Ⅱ)设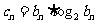 ,求数列
,求数列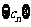 的前
的前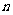 项和
项和 .
.
19.(本小题满分12分)
某数学研究学习小组共有9名学生,其中有3名男生和6名女生,在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言,设每人每次被选中与否均互不影响.
(Ⅰ)求两次汇报都由成员甲发言的概率;
(Ⅱ)求两次汇报男生发言次数不少于女生发言次数的概率.
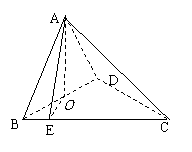
18.(本小题满分12分)
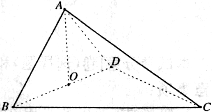 如图,四面体
如图,四面体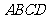 中,
中,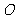 是
是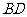 的中点,
的中点,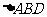 和
和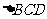 均为等边三角形,
均为等边三角形,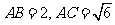 .
.
(I)求证: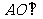 平面
平面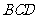 ;
;
(Ⅱ)求二面角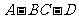 的余弦值;
的余弦值;
(Ⅲ)求点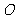 到平面
到平面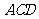 的距离.
的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com