
6、美国弗吉尼亚大学研究人员在有关癌症研究的杂志上发表论文称,他们发现了一种名为RHOGDl2的基因,该基因有助于避免癌细胞扩散,他们发现携带该基因的癌细胞会失去转移能力。该基因的作用最可能的是
A.当这种基因添加到癌细胞后,在癌细胞中表达并产生一种粘连蛋白
B.当这种基因添加到癌细胞后,在癌细胞中表达并产生一种蛋白质,由此使癌细胞迅速分化为其他组织、器官
C.该基因在癌细胞内表达后使癌细胞迅速衰老
D.该基因在癌细胞内表达后使癌细胞的DNA复制受阻,停止细胞分裂
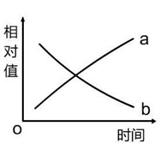 7、下列对右图曲线a和b的描述不正确的是
7、下列对右图曲线a和b的描述不正确的是
A.a和b可分别代表夏季晴天正午时分棉花叶肉细胞中二磷酸
腺苷和NADPH含量的变化
B.a和b可分别代表萌发的植物种子在出土之前蛋白质种类和
干重的变化
C.a和b可分别代表质壁分离过程中植物细胞渗透吸水能力和
原生质体体积的变化
D.a和b可分别代表细胞分化程度和全能性高低的变化
5.随着生物技术的发展,酶在社会生产、生活中的应用越来越广泛。下列说法错误的是
A. 利用酶生产某些化工产品,能显著降低能耗、减少污染、节约成本
B.参与蛋白酶合成分泌的膜性细胞器有核糖体、内质网、高尔基体和线粒体
C. 用于治疗消化不良症的肠溶多酶片含有多种消化酶,但嚼服后会失去疗效
D. 要较长时间保持酶活性,各种酶制剂都应保存在低温的条件下
4、 下图中,甲、乙表示水稻两个品种,A、a和B、b表示分别位于两对同源染色体上的两对等位基因,①-⑧表示培育水稻新品种的过程,则下列说法错误是
下图中,甲、乙表示水稻两个品种,A、a和B、b表示分别位于两对同源染色体上的两对等位基因,①-⑧表示培育水稻新品种的过程,则下列说法错误是
A.①→②过程简便,但培育周期长
B.②和⑦的变异都发生于有丝分裂间期
C.③过程常用的方法是花药离体培养
D.⑤与⑧过程的育种原理不相同
3、下列关于细胞结构和功能的叙述中,不正确的是
A.根尖分生区细胞和叶肉细胞不是都有细胞周期,但化学成分却不断更新
B.抑制膜上载体活性或影响线粒体功能的毒素都会阻碍根细胞吸收无机盐离子
C.只有含叶绿体的细胞才能进行光合作用
D.乳酸菌、酵母菌都含有核糖体和DNA
2、下图表示某生物膜结构,图中A、B、C、D、E、F表示某些物质,a、b、c、d表示物质跨膜运输方式。下列说法正确的是

A.若是根毛细胞的细胞膜,通过中耕松土可促进b物质的吸收
B.若是线粒体膜,b和c过程运输的气体分别是O2 、CO2
C. 若是肝细胞膜,进食后3-4小时,C代表的激素胰岛素将会增多
D.动物细胞吸水膨胀时B的厚度变小,这说明细胞膜具有选择透性
1、抗流感的疫苗,每过几年就要更换新的种类,因为流感病毒已对旧的疫苗产生了高度的抗性,这种抗性最好的解释是
A.病毒因疫苗刺激而产生突变
B.病毒某些结构的用进废退
C.由于生殖隔离造成
D.由于选择作用,使对疫苗有抗性的病毒被保留下来并扩大繁殖
(18)(本题14分)某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(19)(本题14分)已知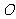 为坐标原点,
为坐标原点, ,
,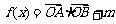 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 的定义域为
的定义域为 ,值域为
,值域为 ,求
,求 的值.
的值.
(20)(本题14分)已知数列{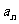 }、{
}、{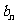 }满足:
}满足: .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式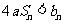 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.
(21)(本题15分)设 为正实数,
为正实数, ,
,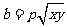 ,
, .
.
(Ⅰ)如果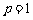 ,则是否存在以
,则是否存在以 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数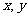 ,试探索当存在以
,试探索当存在以 为三边长的三角形时
为三边长的三角形时 的取值范围.
的取值范围.
(22)(本题15分)已知函数 ,其定义域为
,其定义域为 (
( ),设
),设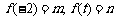 .
.
(Ⅰ)试确定 的取值范围,使得函数
的取值范围,使得函数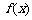 在
在 上为单调函数;
上为单调函数;
(Ⅱ)试判断 的大小并说明理由;
的大小并说明理由;
(Ⅲ)求证:对于任意的 ,总存在
,总存在 ,满足
,满足 ,并确定这样的
,并确定这样的 的个数.
的个数.
2009学年浙江省第一次五校联考

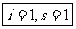 (11)
(11) 的展开式中
的展开式中 的系数为
▲ .
的系数为
▲ .
 (12)如果执行右面的程序框图,那么输出的
(12)如果执行右面的程序框图,那么输出的 ▲ .
▲ .
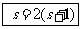
 (13)已知
(13)已知 ,则
,则 的值等于 ▲
.
的值等于 ▲
.
|
|
 (14)等比数列
(14)等比数列 的前
的前 项和为
项和为 ,已知
,已知 ,
,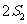 ,
, 成等差数列,
成等差数列,
则 的公比为 ▲ .
的公比为 ▲ .

(15)已知函数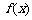 的导函数
的导函数 ,且
,且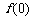 的值为整数,当
的值为整数,当 时,
时,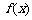 所有可能取的整数值有且只有1个,则
所有可能取的整数值有且只有1个,则 ▲ .
▲ .
(16)数列 中,
中, ,若对任意的正整数
,若对任意的正整数 ,
, 都成立,则
都成立,则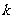 的取值范围为 ▲
.
的取值范围为 ▲
.
(17)给出下列四个结论:
①命题 的否定是“
的否定是“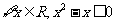 ”;
”;
②“若 则
则 ”的逆命题为真;
”的逆命题为真;
③函数 (x
(x )有3个零点;
)有3个零点;
④对于任意实数x,有 且x>0时,
且x>0时, 则x<0时
则x<0时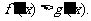
其中正确结论的序号是 ▲ .(填上所有正确结论的序号)
(1)复数 的虚部是( ▲ )
的虚部是( ▲ )
(A)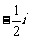 (B)
(B)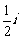 (C)
(C) (D)
(D)
(2)定义集合 ,若
,若 ,则
,则 的子集个数为( ▲ )
的子集个数为( ▲ )
(A)1 (B)2 (C)3 (D)4
(3)已知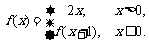 则
则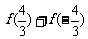 的值等于 ( ▲ )
的值等于 ( ▲ )
(A)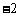 (B)4 (C)2 (D)
(B)4 (C)2 (D)
(4)函数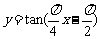 的部分图象如图所示,则
的部分图象如图所示,则 =( ▲ )
=( ▲ )
(A)6
(B)4 (C) (D)
(D)


(5)设随机变量 若
若 ,则
,则 的值为( ▲ )
的值为( ▲ )
(A)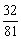 (B)
(B) (C)
(C)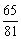 (D)
(D)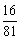
(6)设 ,则
,则 是奇函数的充要条件是( ▲ )
是奇函数的充要条件是( ▲ )
(A) (B)
(B) (C)
(C)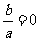 (D)
(D)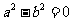
(7)在 中,已知
中,已知 ,给出以下四个论断:
,给出以下四个论断:
①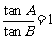 ; ②
; ② ;③
;③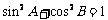 ;④
;④ .
.
其中正确的是( ▲ )
(A)①③ (B)②③ (C)①④ (D)②④
(8)已知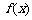 是定义在
是定义在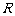 上的奇函数,当
上的奇函数,当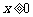 时,
时, ,若
,若 ,则实数
,则实数 的取值范围是( ▲ )
的取值范围是( ▲ )
(A) (B)
(B)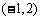 (C)
(C) (D)
(D)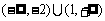
(9)设 是等差数列,从
是等差数列,从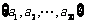 中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( ▲ )
中任取3个不同的数,使这3个数仍成等差数列,则这样不同的等差数列的个数最多有( ▲ )
(A)90 (B)120 (C)180 (D)200
(10)在平面直角坐标系 中,点
中,点 .对于某个正实数
.对于某个正实数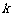 ,存在函数
,存在函数 (
(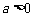 ),使得
),使得 (
(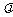 为常数),这里点
为常数),这里点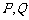 的坐标分别为
的坐标分别为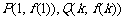 ,则
,则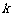 的取值范围为( ▲ )
的取值范围为( ▲ )
(A) (B)
(B) (C)
(C) (D)
(D)
第Ⅱ卷(共100分)
(18)(本题14分)已知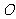 为坐标原点,
为坐标原点,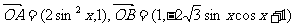 ,
,
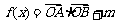 .
.
(Ⅰ)求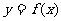 的单调递增区间;
的单调递增区间;
(Ⅱ)若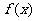 的定义域为
的定义域为 ,值域为[2,5],求
,值域为[2,5],求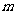 的值.
的值.
(19)(本题14分)设命题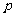 :
: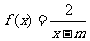 在区间
在区间 上是减函数;
上是减函数;
命题 :
: 是方程
是方程 的两个实根,不等式
的两个实根,不等式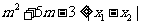 对任意实数
对任意实数 恒成立;若
恒成立;若 为真,试求实数
为真,试求实数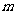 的取值范围.
的取值范围.
(20)(本题14分)已知等比数列 ,公比为
,公比为 ,
, ,
, .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)当 ,求证:
,求证: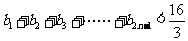
(21)(本题15分)设 为正实数,
为正实数,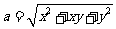 ,
,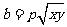 ,
,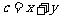 .
.
(Ⅰ)如果 ,则是否存在以
,则是否存在以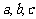 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数 ,试探索当存在以
,试探索当存在以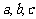 为三边长的三角形时
为三边长的三角形时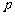 的取值范围.
的取值范围.
(22)(本题15分)设 .
.
(Ⅰ)若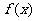 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数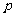 的取值范围;
的取值范围;
(Ⅱ)设 ,且
,且 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数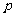 的取值范围.
的取值范围.
2009学年浙江省第一次五校联考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com