
21.(本小题满分15分)
(1)解:设M (x,y),在△MAB中,| AB | = 2,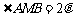 ∴
∴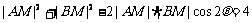 即
即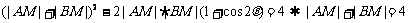 2分
因此点M的轨迹是以A、B为焦点的椭圆,a = 2,c = 1
∴曲线C的方程为
2分
因此点M的轨迹是以A、B为焦点的椭圆,a = 2,c = 1
∴曲线C的方程为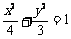 . 6分
. 6分
(2)解法一:设直线PQ方程为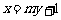 (
( ∈R)
由
∈R)
由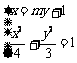 得:
得: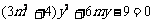 8分
显然,方程①的
8分
显然,方程①的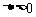 ,设P(x1,y1),Q(x2,y2),则有
,设P(x1,y1),Q(x2,y2),则有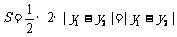
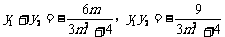
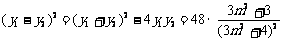 10分
令
10分
令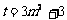 ,则t≥3,
,则t≥3,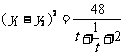 12分
由于函数
12分
由于函数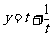 在[3,+∞)上是增函数,∴
在[3,+∞)上是增函数,∴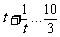 故
故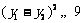 ,即S≤3
∴△APQ的最大值为3 15分
,即S≤3
∴△APQ的最大值为3 15分
解法二:设P(x1,y1),Q(x2,y2),则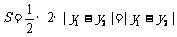 当直线PQ的斜率不存在时,易知S = 3
设直线PQ方程为
当直线PQ的斜率不存在时,易知S = 3
设直线PQ方程为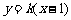 由
由 得:
得: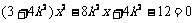 ① 8分
显然,方程①的△>0,则
① 8分
显然,方程①的△>0,则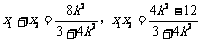 ∴
∴ 10分
10分
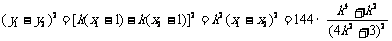 12分
12分
 令
令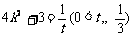 ,则
,则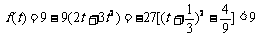 ,即S<3
,即S<3
∴△APQ的最大值为3
20.(本小题满分14分)
解:(1)∵y=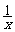 ,∴y'=-
,∴y'=-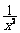 ,又点P的坐标为(t,
,又点P的坐标为(t,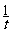 )
)
∴曲线C在点P点的切线斜率为-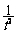
则该切线方程为y-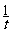 =-
=-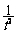 (x-t)
(x-t)
令y=0 xB=2t
xB=2t
由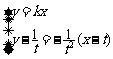
 xA=
xA=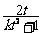
∴xA·xB=2t·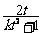 =
=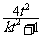
∴f(t)= (t>1).
(t>1).
(2)n≥2时,an=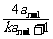 ,
,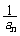 =
=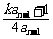 =
=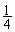 ·
·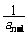 +
+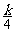
即bn=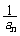 -
-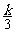 =
=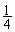 (
(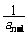 -
-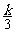 )=
)=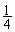 bn-1
bn-1
①当k=3时,bn=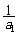 -1=0,∴{bn}是以0为首项的常数列an=1.
-1=0,∴{bn}是以0为首项的常数列an=1.
②当k≠3时,{bn}是以1-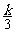 为首项,
为首项,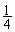 为公比的等比数列
为公比的等比数列
∴bn=(1-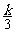 )·(
)·(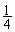 )n-1
)n-1 an=
an=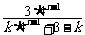
综合①②得
bn=(1-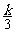 )·(
)·(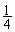 )n-1,an=
)n-1,an= .
.
(3)an-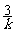 =
= -
-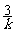 =
=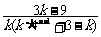
∵1<k<3,∴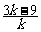 <0,0<
<0,0<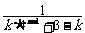 <
<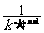
∴an-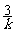 >
>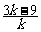 ·
·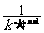 =
=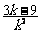 ·
·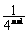
a1+a2+…+an-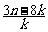 =(a1-
=(a1-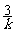 )+(a2-
)+(a2-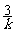 )+…+(an-
)+…+(an-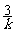 )+8
)+8
>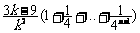 +8>
+8>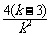 [1-(
[1-(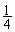 )n]+8
)n]+8
>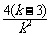 +8=
+8=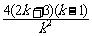
∴1<k<3,∴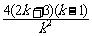 >0
>0
故不等式a1+a2+…+an>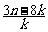 成立.
成立.
19.(本小题满分14分)
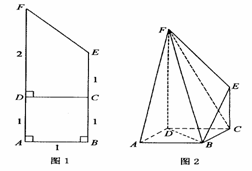
解:∵平面ABCD⊥平面DCEF,ABCD为正方形,DCEF为直角梯形,
∴以DA所在直线为x轴、DC所在直线为y轴、DF所在直线为z轴建立空间直角坐标系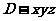 ,则
,则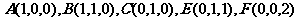 …………2分
…………2分
(1)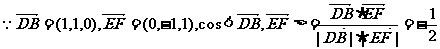 ……2分
……2分
∴异面直线AC与EF所成的角为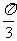 . …………2分
. …………2分
(2) 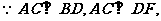 ∴
∴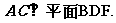
∴平面BDF的法向量为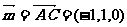 ,…………1分
,…………1分
又设平面BEF的法向量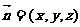 ,
,
则由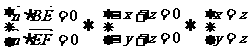 取
取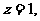
∴平面BEF的法向量为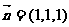 …………2分
…………2分
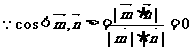
∴二面角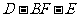 的大小为
的大小为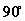 …………2分
…………2分
(3)易知BF的中点H就是球心,HA=HB=HC=HD=HF=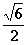 …………2分
…………2分
∴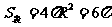 …………1分
…………1分
18.(本小题满分14分)
(1) ∵ , ∴
, ∴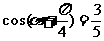 ……………3分
……………3分
又∵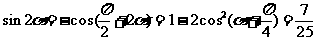 ……5分
……5分
∴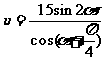 =7 …………………………7分
=7 …………………………7分
(2) 由题意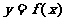 关于直线
关于直线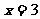 对称
对称
∴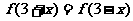 …………………………………………9分
…………………………………………9分
∴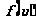 =
=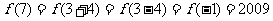 ……………14分
……………14分
17. ①②③⑤
15.
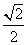 16.
4n-1
16.
4n-1
13.
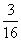 14.
0
14.
0
11.
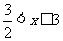 12.
12. 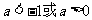
22.(本小题满分15分)
 余姚中学
高三数学(理)第二次质量检测答案
余姚中学
高三数学(理)第二次质量检测答案
21.(本小题满分15分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com