
4.求二面角的方法很多,概括起来有两类,一类是作平面角,一类是不作平面角。作平面角又有直接作和间接作两种,形形色色的方法都是在做一件事:作二面角的棱的垂面;而不作平面角,要么建系用法向量求,要么用公式cos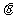 =
=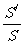 (其中S表示平面
(其中S表示平面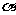 内的封闭图形C的面积,S/表示C在平面
内的封闭图形C的面积,S/表示C在平面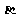 内的射影C/的面积,
内的射影C/的面积,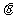 表示
表示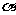 与
与 所成的锐二面角的大小)。二面角
所成的锐二面角的大小)。二面角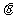 的范围(00,1800)。如cos
的范围(00,1800)。如cos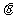 =-
=-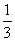 ,则
,则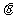 = arccos(-
= arccos(-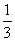 )=
)=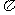 - arccos
- arccos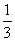 。
。
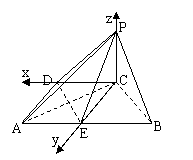
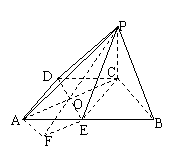 [举例]如图在四棱锥P-ABCD中,底面ABCD是
[举例]如图在四棱锥P-ABCD中,底面ABCD是
直角梯形,∠ADC=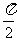 ,AB∥CD,PC⊥面ABCD,
,AB∥CD,PC⊥面ABCD,
PC=AD=DC=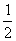 AB,E为线段AB的中点。
AB,E为线段AB的中点。
(1)求证:平面PAC⊥平面PDE;
(2)求二面角A-PE-D的大小。
解析:(1)在直角梯形ABCD中,容易知道四边形AECF是
正方形,∴DE⊥AC,又DE⊥PC∴DE⊥面PAC,∴面PDE⊥面PAC;(2)记PC=a,
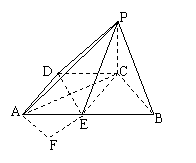 方法一:用三垂线定理作二面角的平面角。记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,过A作PO的垂线交PO(的延长线)于F,则AF⊥面PDE,即F是A在面PDE内的射影,又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,∴∠AEF是二面角A-PE-D的平面角;在⊿PAO中有面积相等不难算出AF=
方法一:用三垂线定理作二面角的平面角。记AC、DE交于O,连PO,PO是相互垂直的平面PDE和PAC的交线,过A作PO的垂线交PO(的延长线)于F,则AF⊥面PDE,即F是A在面PDE内的射影,又容易证明AE⊥面PEC,则AE⊥PE,于是FE⊥PE,∴∠AEF是二面角A-PE-D的平面角;在⊿PAO中有面积相等不难算出AF=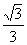 a,而AE=a,在Rt⊿AFE中,∠AEF=arcsin
a,而AE=a,在Rt⊿AFE中,∠AEF=arcsin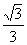 。注:用三垂线定理作二面角的平面角,是作二面角的平面角的最常用、最重要的方法。其过程概括为:找一垂--找(作)一个面内一点P在另一个面内的射影P/,作二垂--过P(或P/)作二面角棱l的垂线,垂足为Q,连三垂--连P/Q,则l⊥P/Q,于是∠PQ P/为二面角的平面角;计算该角在直角三角形内进行;在上述过程中,“找一垂”是关键。方法二:射影“悬空”作二面角的平面角
。注:用三垂线定理作二面角的平面角,是作二面角的平面角的最常用、最重要的方法。其过程概括为:找一垂--找(作)一个面内一点P在另一个面内的射影P/,作二垂--过P(或P/)作二面角棱l的垂线,垂足为Q,连三垂--连P/Q,则l⊥P/Q,于是∠PQ P/为二面角的平面角;计算该角在直角三角形内进行;在上述过程中,“找一垂”是关键。方法二:射影“悬空”作二面角的平面角
注意到AE⊥PE,记点A在面PDE内的射影为F
(无须知道点F的确切位置),连EF,则PE⊥FE,于是
∠AEF是二面角A-PE-D的平面角;以下问题化归
到求AF的长度(即A点到面PDE的距离)上。以下
用“等积转换”求AF,计算略。
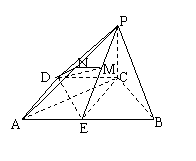 方法三:利用平面图形的有关性质作二面角的平面角
方法三:利用平面图形的有关性质作二面角的平面角
注意到DP=DE=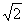 a,取PE的中点M,则PE⊥DM,
a,取PE的中点M,则PE⊥DM,
又容易知道AE⊥PE,取PA的中点N,连NM,则
NM∥AE,∴PE⊥MN,于是∠NMD为二面角A-PE-D
的平面角;以下在⊿DMN中,用余弦定理求∠NMD,
计算略。
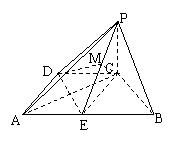 方法四:用割补法求。视二面角A-PE-D为二面角A-PE-C
方法四:用割补法求。视二面角A-PE-D为二面角A-PE-C
与二面角D-PE-C的差。对二面角A-PE-C,
∵ AE⊥面PEC,∴面AEP⊥面PEC,
即二面角A-PE-C为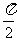 ;对二面角D-PE-C,点C是点D
;对二面角D-PE-C,点C是点D
在面PEC内的射影,取BE的中点M,∵CP=CE=a,
∴PE⊥MC,于是有:PE⊥MD,则∠DMC为二面角D-PE-C的平面角,
 在Rt⊿DCM中,∠DMC=arctan
在Rt⊿DCM中,∠DMC=arctan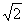 ,∴二面角A-PE-D的大小为
,∴二面角A-PE-D的大小为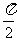 - arctan
- arctan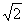 。
。
注:在求钝二面角时“割补法”往往很有效。
方法五:用平面的“法向量”求
∵CP⊥CE, CP⊥CD, CE⊥CD,故可以C为原点,
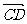 、
、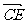 、
、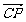 分别为x、y、z轴建立空间
分别为x、y、z轴建立空间
直角坐标系。A(a,a,0)、D(a,0,0)、E(0,a,0)、
P(0,0,a),则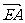 =(a,0,0),
=(a,0,0),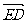 =(a,-a,0),
=(a,-a,0),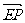 =(0,-a,a)
=(0,-a,a)
由此不难求出平面PAE的法向量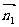 =(0,1,1), 平面PAE的法向量
=(0,1,1), 平面PAE的法向量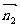 =(1,1,1)
=(1,1,1)
 则有:cos<
则有:cos<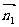 ,
,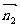 >=
>=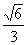 ,∴二面角A-PE-D的大小为arccos
,∴二面角A-PE-D的大小为arccos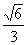 。注:用“法向量”求二面角有一处严重的不足:二面角两个面的法向量的夹角
。注:用“法向量”求二面角有一处严重的不足:二面角两个面的法向量的夹角
未必等于二面角,也可能与二面角互补,这取决于法向量
的方向,而确定法向量的方向却是中学生力不能及的。
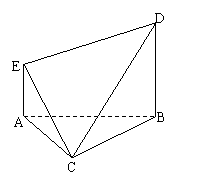
[巩固] 如图,在多面体ABCDE中,AE⊥面ABC,
BD∥AE,且AC=AB=BC=BD=2,AE=1,求面CDE与
面CAB所成的锐二面角.
3. 直线与平面所成的角要“抓住”直线在平面内的射影,然后在直角三角形内求得;直线与平面所成的角是直线与平面内任意直线所成角的最小值。线面角的范围:[00,900]。
直线与平面所成的角要“抓住”直线在平面内的射影,然后在直角三角形内求得;直线与平面所成的角是直线与平面内任意直线所成角的最小值。线面角的范围:[00,900]。
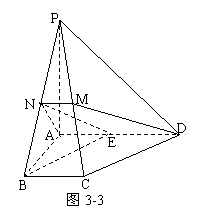
[举例1] 在如图3-1所示的几何体中,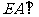 平面
平面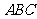 ,
,
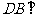 平面
平面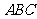 ,
,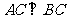 ,且
,且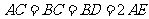 ,
,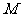 是
是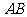 的中点.求
的中点.求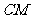 与平面
与平面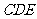 所成的角.
所成的角.
(07高考浙江理16)
解析:方法一:“找射影”。过M作MF⊥ED于F,连CF,
由CM⊥AB,CM⊥AE得CM⊥面ABDE,故CM⊥ED,
∴ED⊥面CMF,于是有面CED⊥面CMF于CF,过M作MH⊥CF
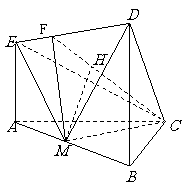 于H,则MH⊥面CED,∴∠MCH为
于H,则MH⊥面CED,∴∠MCH为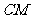 与平面
与平面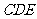 所成的角;
所成的角;
设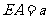 ,
,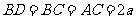 ,
,
在直角梯形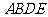 中,
中,
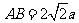 ,
,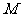 是
是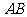 的中点,
的中点,
所以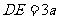 ,
,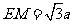 ,
,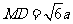 ,
,
得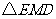 是直角三角形,其中
是直角三角形,其中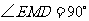 ,∴MF=
,∴MF=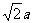
在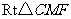 中,CM=MF,∴
中,CM=MF,∴ 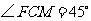 ,故
,故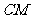 与平面
与平面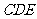 所成的角是
所成的角是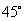 .
.
 注:“作垂面”是求作点M在面
注:“作垂面”是求作点M在面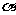 内的射影的最重要、最常用的方法,其过程是:过M点作平面
内的射影的最重要、最常用的方法,其过程是:过M点作平面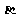 ⊥
⊥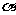 于
于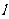 ,则M在面
,则M在面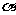 内的射影M/∈
内的射影M/∈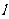 。
。
方法二:“建系”。如图,以点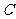 为坐标原点,以
为坐标原点,以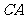 ,
,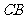
分别为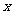 轴和
轴和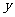 轴,过点
轴,过点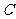 作与平面
作与平面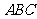 垂直的直线为
垂直的直线为
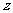 轴,建立直角坐标系
轴,建立直角坐标系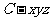 ,设
,设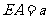 ,则
,则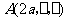 ,
,
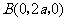 ,
,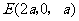 .
.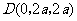 ,
,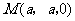 .
.
设向量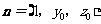 与平面
与平面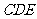 垂直,
垂直,
则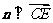 ,
,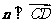 ,即n·
,即n·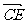 =0 , n·
=0 , n·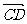 =0,∵
=0,∵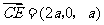 ,
,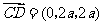 ,
,
得: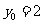 ,
,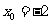 ,即
,即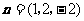 ,由向量夹角公式得:cos< n,
,由向量夹角公式得:cos< n,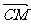 >=
>=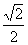 ,
,
直线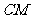 与平面
与平面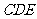 所成的角
所成的角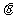 是
是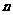 与
与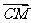 夹角的余角,所以
夹角的余角,所以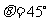 ,
,
故直线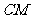 与平面
与平面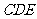 所成的角是
所成的角是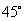 .
.
注:线与面的法向量所成的角与线面角互余;注意到线面角不为钝角,故:AB与面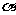 所成的角为:arcsin
所成的角为:arcsin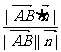 (
(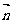 为面
为面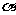 的法向量)。用法向量求线面角,以计算代替说理(找射影),最大限度地实现了“去逻辑化”,为疏于逻辑思维的同学求线面角提供了一条相对方便的路径;但是,并非所有的空间形体都可以建立适当的坐标系。
的法向量)。用法向量求线面角,以计算代替说理(找射影),最大限度地实现了“去逻辑化”,为疏于逻辑思维的同学求线面角提供了一条相对方便的路径;但是,并非所有的空间形体都可以建立适当的坐标系。
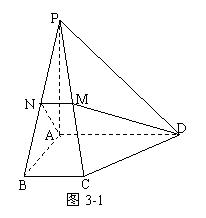 [举例2]如图3-1,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点. 求CD与平面ADMN所成的角。
[举例2]如图3-1,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点. 求CD与平面ADMN所成的角。
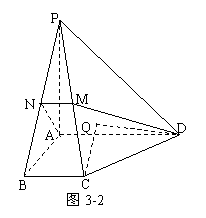
解析:确定C点在面ADMN上的射影Q的位置很困难。方法一:“射影悬空”。先不管Q点的位置,∠CDQ为CD与平面ADMN所成的角,入图3-2;记BC=a,在Rt⊿CQD中,CD=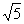 a,只需求出CQ(C到面ADMN的距离)即可,记为h;注意到
a,只需求出CQ(C到面ADMN的距离)即可,记为h;注意到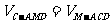 ,不难知道
,不难知道
⊿AMD中AD边上的高为AN,AN=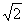 a,∴
a,∴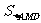 =
=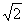 a2;
a2;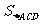 =2a2,M到面ACD的距离为a,
=2a2,M到面ACD的距离为a,
∴h=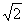 a,故在Rt⊿CQD中,∠CDQ= arcsin
a,故在Rt⊿CQD中,∠CDQ= arcsin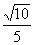 。注:射影“悬空”求线面角的“革命”性意义在于绕开了求线面角中最困难的一步--确定射影的位置,把问题化归为求点到面的距离;而求点到面的距离可以通过“等积转换”实现,并不需要知道射影的确切位置。
。注:射影“悬空”求线面角的“革命”性意义在于绕开了求线面角中最困难的一步--确定射影的位置,把问题化归为求点到面的距离;而求点到面的距离可以通过“等积转换”实现,并不需要知道射影的确切位置。
方法二:“平移”线段。取AD中点E,连BE,如图3-3,易见:BE∥CD,∴CD与平面ADMN所成的角即BE 与平面ADMN所成的角;不难证明:BN⊥AN,BN⊥AC,∴BN⊥面ADMN,即点B在面ADMN上的射影为N,∠BEN为BE 与平面ADMN所成的角;记BC=a,BN=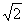 a,BE=
a,BE=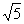 a,在Rt⊿BNE中,∠BEN=arcsin
a,在Rt⊿BNE中,∠BEN=arcsin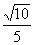 。本题也可以“建系”求,略。
。本题也可以“建系”求,略。
[巩固1]太阳光线斜照地面,地面上与太阳光线成600角的直线有_________条?若太阳光线与地面成60°角时,要使一根长2米的竹竿影子最长,则竹竿与地面所成的角为 。
[巩固2] 在三棱锥P-ABC中,AB⊥BC,AB=BC,PA=2BC,点O是AC的中点,OP⊥底面ABC.求直线PA与平面PBC所成角的大小.
2.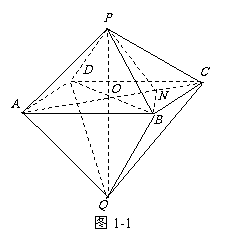 研究异面直线所成的角通常有两种方法。①通过平移使之成为一个平面角,然后解三角形求得;②在空间直角坐标系中利用向量的夹角公式。[注意] 异面直线所成角的范围是:(00,900], 如: cos <
研究异面直线所成的角通常有两种方法。①通过平移使之成为一个平面角,然后解三角形求得;②在空间直角坐标系中利用向量的夹角公式。[注意] 异面直线所成角的范围是:(00,900], 如: cos <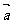 ,
,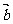 >=-
>=-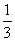 ,则异面直线 a, b所成的角为 arccos
,则异面直线 a, b所成的角为 arccos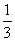 。
。
[举例] 如图, 已知两个正四棱锥
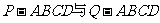 的高分别为1和2,
的高分别为1和2,
 ,(Ⅰ) 证明:
,(Ⅰ) 证明:  ;
;
(Ⅱ) 求异面直线AQ与PB所成的角;
解析:(Ⅰ)记AC、BD交于O,连PO、QO,
则PO⊥面ABCD,QO⊥面ABCD,∴P、Q、O
共线,PQ⊥面ABCD;
(Ⅱ)方法一:“平移”:注意到AC、PQ交于O,
取OC的中点N,连结PN,BN,
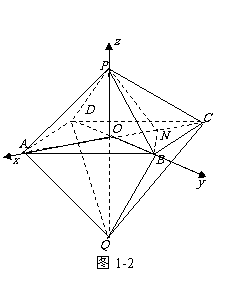 ∵
∵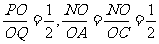 ,∴
,∴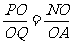 ,故AQ∥PN. ∠BPN是异面直线AQ与PB
,故AQ∥PN. ∠BPN是异面直线AQ与PB
所成的角(或其补角). 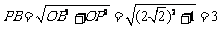
∵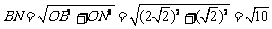
∴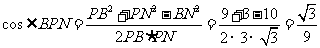
故异面直线AQ与PB所成的角是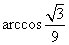 .
.
方法二:“建系”:由题设知,ABCD是正方形,
∴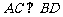 .由(I),
.由(I),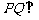 平面
平面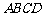 ,故
,故
可以分别以直线CA、DB、QP为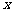 轴,
轴,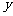 轴,
轴,
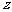 轴建立空间直角坐标系(如图1-2),由题设,
轴建立空间直角坐标系(如图1-2),由题设,
相关各点的坐标分别是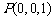 ,
,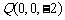 ,
,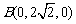 ,
,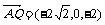 ,
,
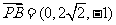 ,于是
,于是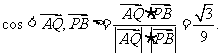
注:在“平移”时常用到一些平面图形的性质,如:三角形的中位线、梯形中位线、平行四边形、平行线分线段成比例定理的逆定理甚至三角形相似等。
[巩固1]异面直线 a, b所成的角为600,则过空间中一点P与a, b都成300的直线有几条?与a, b都成500的直线有几条?与a, b都成600的直线有几条?与a, b都成700的直线有几条?[变形]过大小为600的二面角外一点P作与它的两个面都成600的直线有几条?
 [巩固2
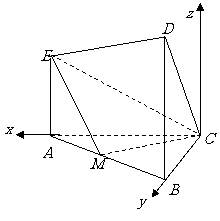
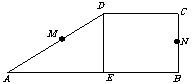
]设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
[巩固2
]设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
1.解立几题要有化平几思想:所有求空间角与距离的问题最终都要转化到平面上求解,有时还可以将要求的角(或线段)所在的平面分离出来,这样清楚醒目,便于求解,不易出错。
4.关注概率与其它知识点的“交汇”,如数列、不等式、解析几何等。
[举例1]设集合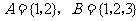 ,分别从集合
,分别从集合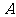 和
和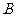 中随机取一个数
中随机取一个数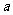 和
和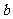 ,确定平面上的一个点
,确定平面上的一个点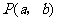 ,记“点
,记“点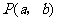 落在直线
落在直线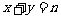 上”为事件
上”为事件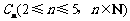
,若事件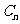 的概率最大,则
的概率最大,则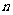 的所有可能值为( ) (07高考山东文12)
的所有可能值为( ) (07高考山东文12)
A.3 B.4 C.2和5 D.3和4
解析:点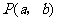 落在直线
落在直线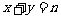 上,即
上,即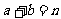 ;集合
;集合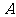 和
和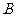 中随机取一个数
中随机取一个数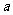 和
和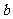
有6种方法,它们是等可能的,其中使得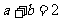 有1种,使得
有1种,使得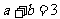 有2种,使得
有2种,使得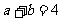 有2种,使得
有2种,使得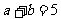 有1种;故使得事件
有1种;故使得事件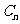 的概率最大的
的概率最大的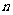 可能为3和4。
可能为3和4。
[举例2] 正四面体的各顶点为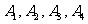 ,进入某顶点的动点 X不停留在同一个顶点上,每隔1秒钟向其他三个顶点以相同的概率移动。
,进入某顶点的动点 X不停留在同一个顶点上,每隔1秒钟向其他三个顶点以相同的概率移动。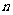 秒后X在
秒后X在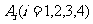 的概率用
的概率用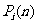 (n=0,1,2……)
表示。当
(n=0,1,2……)
表示。当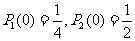 ,
,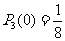 ,
,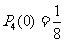 时,
时,
(1)求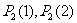 ;
(2)求
;
(2)求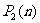 与
与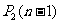 的关系(
的关系(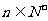 )
)
(3)求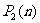 关于n的表达式, (4)求
关于n的表达式, (4)求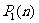 关于n的表达式
关于n的表达式
解析: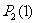 即1秒后动点在
即1秒后动点在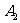 的概率,它有三种情况;①开始时(0秒)在
的概率,它有三种情况;①开始时(0秒)在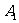 ,1秒后移动到
,1秒后移动到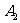 ;由题意知,每隔1秒钟动点
X从一个顶点移动到另一个顶点的概率均为
;由题意知,每隔1秒钟动点
X从一个顶点移动到另一个顶点的概率均为 ;所以这种情况的概率为:
;所以这种情况的概率为: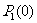 ×
× =
=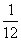 ;②开始时在
;②开始时在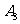 ,1秒后移动到
,1秒后移动到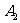 ;其概率为:
;其概率为:
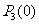 ×
× =
=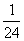 ;③开始时在
;③开始时在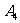 ,1秒后移动到
,1秒后移动到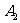 ;其概率为:
;其概率为: ×
× =
=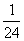 ;
;
又这种情况互斥,∴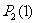 =
=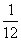 +
+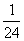 +
+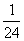 =
=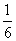 。我们设想一下,如果仍然按这个办法计算
。我们设想一下,如果仍然按这个办法计算
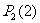 ,将不胜其烦,因为首先要算
,将不胜其烦,因为首先要算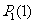 、
、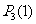 、
、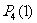 ;事实上1秒后动点在
;事实上1秒后动点在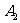 ,即开始时(0秒)动点不在
,即开始时(0秒)动点不在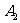 ,其概率为:1-
,其概率为:1-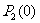 =
=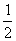 ,而每隔1秒钟动点
X从一个顶点移动到另一个顶点的概率均为
,而每隔1秒钟动点
X从一个顶点移动到另一个顶点的概率均为 ;所以
;所以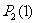 =
=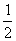 ×
× =
=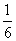 。类似的,2秒后动点在
。类似的,2秒后动点在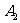 ,即1秒后动点不在
,即1秒后动点不在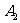 ,其概率为:1-
,其概率为:1-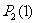 =
=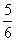 ,∴
,∴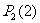 =
=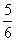 ×
× =
=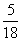 ;
;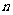 秒后动点在
秒后动点在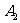 ,即
,即 秒后动点不在
秒后动点不在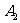 ,其概率为:1-
,其概率为:1-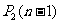 ,∴
,∴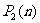 =[1-
=[1-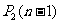 ]×
]× 。至此,问题化归为数列问题。即:已知数列{
。至此,问题化归为数列问题。即:已知数列{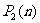 }满足:
}满足: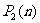 =-
=-
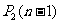 +
+ ,求通项公式。用待定系数法构造等比数列,设
,求通项公式。用待定系数法构造等比数列,设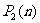 +
+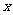 =-
=- [
[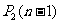 +
+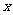 ],得
],得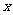 =
=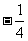 ,可见
,可见
数列{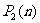
 }是以-
}是以- 为公比的等比数列,其首项为
为公比的等比数列,其首项为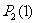
 =
=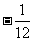
∴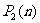
 =
=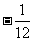
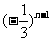 ,
,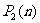 =
=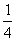
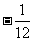
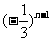 。
。
完全类似地,可得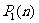 =-
=-
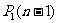 +
+ ,于是有
,于是有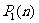
 =-
=- [
[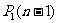
 ]
]
但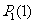
 =0,∴数列{
=0,∴数列{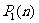 }是常数列,即
}是常数列,即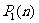 =
=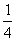 。
。
点评:本题的关键是:第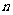 秒后动点在某一顶点即意味着第
秒后动点在某一顶点即意味着第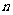
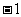 秒后动点不在该顶点,由此反映的它们的概率之间的关系正是数列的前后项之间的关系即递推关系,于是从概率问题自然地过渡到数列问题,再用数列的办法解决之。
秒后动点不在该顶点,由此反映的它们的概率之间的关系正是数列的前后项之间的关系即递推关系,于是从概率问题自然地过渡到数列问题,再用数列的办法解决之。
[巩固1]已知一组抛物线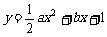 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是 ( )
(07高考四川理12)
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是 ( )
(07高考四川理12)
(A)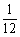 (B)
(B)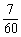 (C)
(C)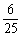 (D)
(D)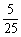
[巩固2]位于坐标原点的一个质点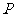 按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是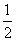 ,质点
,质点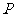 移动五次后位`于点
移动五次后位`于点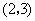 的概率是 ( ) (07高考山东理12)
的概率是 ( ) (07高考山东理12)
A.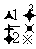 B.
B. C.
C.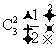 D.
D.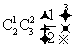
[巩固3]有人玩掷硬币走跳棋的游戏,已知硬币出现正反面的概率都是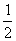 ,棋盘上标有第0站,第1站,…,第100站,一枚棋子开始在第0站,棋手每掷一次硬币棋子向前跳动一次,若掷出正面,棋子向前跳一站(从n到n+1),若掷出反面,棋子向前跳两站(从n到n+2),直到棋子跳到第99站(胜利大本营),或跳到第100站(失败集中营)时该游戏结束,设棋子跳到第n站的概率为P(n);(1)求P(1), P(2),P(3);(2)求证:数列{P(n)-P(n-1)}是等比数列 (n∈N﹡,n≤99);(3)求P(99)及P(100)的值。
,棋盘上标有第0站,第1站,…,第100站,一枚棋子开始在第0站,棋手每掷一次硬币棋子向前跳动一次,若掷出正面,棋子向前跳一站(从n到n+1),若掷出反面,棋子向前跳两站(从n到n+2),直到棋子跳到第99站(胜利大本营),或跳到第100站(失败集中营)时该游戏结束,设棋子跳到第n站的概率为P(n);(1)求P(1), P(2),P(3);(2)求证:数列{P(n)-P(n-1)}是等比数列 (n∈N﹡,n≤99);(3)求P(99)及P(100)的值。
3.要准确理解题意,吃透其中的“关键词”,如: “至多”、“至少”、“恰有“、“不全是”、“全不是”等;要能读出题目的“言下之意”。
[举例1]在医学生物试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(I)求笼内恰好剩下1只果蝇的概率;
(II)求笼内至少剩下5只果蝇的概率.(07高考安徽文19).
解析:设笼内恰好剩下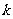 只果蝇的事件为
只果蝇的事件为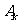
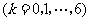 .
.
(I)笼内恰好剩下1只果蝇即第7只飞出的是苍蝇,而前6只飞出的蝇子中有1只苍蝇、5只果蝇;基本事件有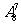 种,它们是等可能的,其中目标事件有
种,它们是等可能的,其中目标事件有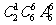 种,
种,
故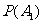 =
=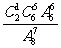 =
=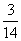 ;(II)笼内至少剩下5只果蝇为事件
;(II)笼内至少剩下5只果蝇为事件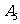 +
+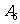 ,
,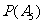 =
=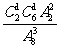
=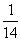 ,
,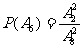 =
=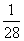 ,又事件
,又事件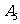 、
、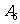 互斥,故P(
互斥,故P(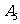 +
+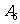 )=P(
)=P(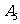 )+P(
)+P(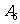 )=
)=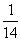 +
+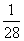
=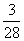 ;答:笼内恰好剩下1只果蝇的概率为
;答:笼内恰好剩下1只果蝇的概率为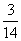 ,笼内至少剩下5只果蝇的概率
,笼内至少剩下5只果蝇的概率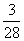 。
。
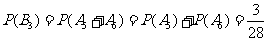 .
.
[举例2]甲、乙两人个有4张卡片,现以掷硬币的形式进行游戏。当出现正面朝上时,甲赢得乙一张卡片,否则乙赢得甲一张卡片,如果某人已赢得所有卡片,则游戏立即终止,求掷币次数不大于6时游戏恰好终止的概率。
解析:显然,至少需掷币4次,游戏才可能终止;现要求掷币次数不大于6时游戏终止,看似有三种情况,即掷币次数分别为4、5、6,但事实上掷币5次游戏终止的情况是不可能出现的:因为,首先前4次不可能都为正面或反面(否则掷币4次后游戏已经终止),若前4次中有1次反面而其它4次都为正面,此时甲手中有7张卡片,乙手中有1张卡片,游戏尚未终止。设掷币4次游戏终止的事件为A,P(A)=2×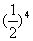 =
=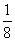 ;掷币6次游戏终止的事件为B,则前4次中有1次反面而其它5次都为正面,或前4次中有1次正面而其它5次都为反面,∴P(B)=2×
;掷币6次游戏终止的事件为B,则前4次中有1次反面而其它5次都为正面,或前4次中有1次正面而其它5次都为反面,∴P(B)=2×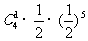 =
=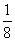 ,有又掷币次数不大于6时游戏恰好终止为A+B ,且
,有又掷币次数不大于6时游戏恰好终止为A+B ,且
A、B互斥,∴P(A+B)=P(A)+P(B)=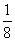 +
+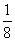 =
=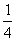 ;
;
[巩固1] 甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束,设各局比赛相互间没有影响,求(Ⅰ)前三局比赛甲队领先的概率;
(Ⅱ)本场比赛乙队以3:2取胜的概率.(精确到0.001)
[巩固2] 10个球中有一个红球,有放回的抽取,每次取出一球,直到第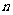 次才取得
次才取得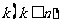 次红球的概率为( )
次红球的概率为( )
A.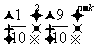 ,B.
,B.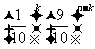 C.
C.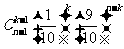 D.
D.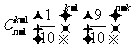
[巩固3] 从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件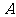 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率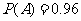 .
.
(1)求从该批产品中任取1件是二等品的概率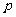 ;
;
(2)若该批产品共100件,从中任意抽取2件,求事件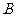 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率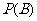 .(07高考全国卷Ⅱ理19)
.(07高考全国卷Ⅱ理19)
2.“等可能性事件”的概率为“目标事件的方法数”与“基本事件的方法数”的商,注意区分“有放回”和“不放回”;“互斥事件”的概率为各事件概率的和;“相互独立事件”的概率为各事件概率的积;若事件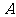 在一次试验中发生的概率是
在一次试验中发生的概率是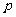 ,则它在
,则它在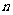 次“独立重复试验”中恰好发生
次“独立重复试验”中恰好发生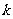 次的概率为
次的概率为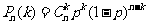 ;若事件
;若事件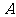 发生的概率是
发生的概率是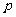 ,则
,则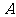 的“对立事件”
的“对立事件”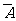 发生的概率是1-
发生的概率是1-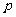 等。有的同学只会列式子,不会“说”事件,那就根据你列的式子“说”:用排列(组合)数相除的是“等可能性事件”,用概率相加的是“互斥事件”,用概率相乘的是“相互独立事件”,用
等。有的同学只会列式子,不会“说”事件,那就根据你列的式子“说”:用排列(组合)数相除的是“等可能性事件”,用概率相加的是“互斥事件”,用概率相乘的是“相互独立事件”,用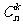 的是“独立重复试验”,用“1减”的是“对立事件”。
的是“独立重复试验”,用“1减”的是“对立事件”。
[举例1] 已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率; (07高考天津文18)
解析:(Ⅰ)设“从甲盒内取出的2个球均为红球”为事件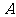 ;从甲盒内取出2个球(基本事件)有
;从甲盒内取出2个球(基本事件)有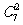 种方法,它们是等可能的,其中2个球均为红球(目标事件)的有
种方法,它们是等可能的,其中2个球均为红球(目标事件)的有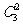 种,∴
种,∴
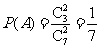 ;设“从乙盒内取出的2个球均为红球”为事件
;设“从乙盒内取出的2个球均为红球”为事件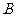 ,有
,有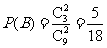 ;
;
而“取出的4个球均为红球”即事件A、B同时发生,又事件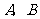 相互独立,
相互独立,
∴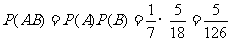 .
.
(Ⅱ)设“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个红球为黑球”为事件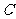 ,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件
,“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件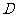 .
.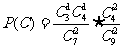 =
=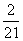 ,
,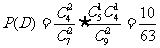 ;
;
而“取出的4个红球中恰有4个红球”即事件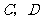 有一个发生,又事件
有一个发生,又事件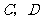 互斥,∴
互斥,∴
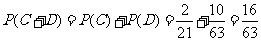
答:取出的4个球均为红球的概率是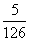 ,取出的4个球中恰有1个红球的概率是
,取出的4个球中恰有1个红球的概率是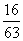 。
。
[举例2] 某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,求这3人中至少有2人参加过培养的概率.(07高考湖南文17)
解析:任选1名下岗人员,记“该人参加过财会培训”为事件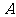 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件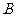 ,由题设知,事件
,由题设知,事件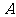 与
与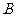 相互独立,且
相互独立,且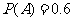 ,
,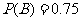 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训即事件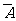 、
、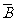 同时发生,其概率是
同时发生,其概率是
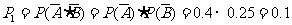
所以该人参加过培训的概率是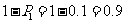 .
.
解法二:任选1名下岗人员,设该人只参加过一项培训为事件C,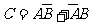 ,
,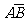 与
与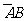
互斥,∴P(C)=P(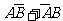 )=P(
)=P(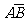 )+P(
)+P(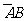 )=0.6×0.25+0.4×0.75=0.45;
)=0.6×0.25+0.4×0.75=0.45;
该人参加过两项培训为事件D,P(D)=P(AB)=0.6×0.75=0.45
该人参加过培训即C、D有一个发生,且C、D互斥,∴其概率为P(C+D)=P(C)+P(D)=0.9;
(II)解法一:设任选3名下岗人员,3人中恰有2人参加过培训为事件E,E是独立重复实验,其中n=3,k=2,p=0.9,∴P(E)=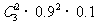 =0.243,
=0.243,
设任选3名下岗人员,3人都参加过培训为事件F,P(F)=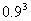 =0.729.
=0.729.
“3人中至少有2人参加过培训”即E、F有一个发生,又E、F互斥,∴它的概率是:P(E+F)
=P(E)+P(F)=0.243+0.729=0.972;
解法二:设任选3名下岗人员,3人中恰有1人参加过培训为事件G,P(G)=
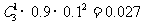 ;设任选3名下岗人员,3人都没有参加过培训为事件H,P(H)=
;设任选3名下岗人员,3人都没有参加过培训为事件H,P(H)=
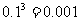 ;“3人中至少有2人参加过培训”即
;“3人中至少有2人参加过培训”即 ,
,
P( )=
)=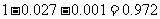 ;
;
答:任选1名下岗人员该人参加过培训的概率是0.9,任选3名下岗人员,这3人中至少有2人参加过培养的概率是0.972
[巩固1] 某条公共汽车线路沿线共有11个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有6位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
(I)这6位乘客在其不相同的车站下车的概率;
(II)这6位乘客中恰有3人在终点站下车的概率;(07高考北京文18)
[巩固2] 设甲、乙两人每次射击命中目标的概率分别为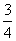 和
和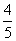 ,且各次射击相互独立.
,且各次射击相互独立.
(Ⅰ)若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
(Ⅱ)若甲、乙各射击两次,求两人命中目标的次数相等的概率.(07高考重庆文17)
1. 解概率应用题要学会“说”:首先是记事件,其次是对事件做必要的分析,指出事件的概率类型,包括“等可能性事件”、“互斥事件”、“相互独立事件”、“独立重复试验”、“对立事件”等;然后是列式子、计算,最后别忘了作“答”。
9.研究多项式的“系数和”一般用“赋值法”。若多项式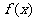 =a0+a1x+a2x2+a3x3+……anxn,则展开式中所有项的系数和=f(1),其中奇数项的系数和=
=a0+a1x+a2x2+a3x3+……anxn,则展开式中所有项的系数和=f(1),其中奇数项的系数和= ,偶数项的系数和=
,偶数项的系数和=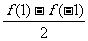 ;展开式中的常数项=f(0)。
;展开式中的常数项=f(0)。
[举例]设(1+2x)2(1-x)5=a0+a1x+a2x2+…+a7x7,则a1-a2+a3-a4+a5-a6+a7= .
解析:令x=1得a0+a1+a2+a3+a4+a5+a6+a7=0 ①
令x= -1得a0-a1+a2-a3+a4-a5+a6-a7=32 ② 由①②解得:a0 +a2 +a4 +a6=16,
a1+ a3+ a5+a7= -16,在令x=0得a0=1,∴a2 +a4 +a6=15,∴a1-a2+a3-a4+a5-a6+a7=-31。
[举例2]已知(1+x)+(1+x)2+(1+x)3+……+(1+x)n=a0+a1x+a2x2+a3x3+……+anxn,若a1+a2+……+an-1=29-n,则正整数n=____________
解析:只有(1+x)n 的展开式中才有含xn 的项,它的系数为1,令x=0得a0=n,
令x=1得a0+a1+a2+……+an-1+an=2+22+23+……+2n=2n+1-2,∴a1+a2+……+an-1=2n+1-2-1-n
∴2n+1-3-n=29-n得n=4.
[巩固1]设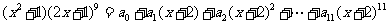 ,
,
则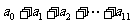 的值为( )(07高考江西文科第5题)
的值为( )(07高考江西文科第5题)
A. B.
B. C.
C. D.
D.
[巩固2]已知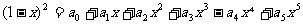 ,则
,则
(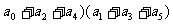 的值等于
. (安徽文科第12题)
的值等于
. (安徽文科第12题)
[迁移]设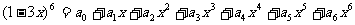 , 则集合
, 则集合
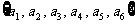 含2 个元素的所有子集的元素总和为
( )
含2 个元素的所有子集的元素总和为
( )
A 640 B 630 C 320 D 315
8.注意辨析“系数”与“二项式系数”的区别;二项式系数和=2n,其中奇数项的二项式系数和=偶数项的二项式系数和=2n-1,二项式系数先增后减,并关于中间项“对称”,二项展开式中,中间项二项式系数最大;求二项展开式中系数绝对值最大的项,用“夹逼法”。
[举例]若 展开式中奇数二项式系数和为8192,则展开式中系数最大的项为
。
展开式中奇数二项式系数和为8192,则展开式中系数最大的项为
。
解析: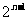 =8192得
=8192得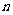 =14,则
=14,则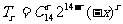 ,由于
,由于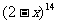 展开式中各项系数正负相间,故先求其展开式中系数绝对值最大的项,记为第
展开式中各项系数正负相间,故先求其展开式中系数绝对值最大的项,记为第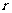 +1项,于是有:
+1项,于是有:
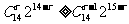 ①,
①,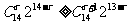 ②;由①②解得:4≤
②;由①②解得:4≤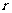 ≤5;
≤5;
又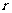 =5时系数为负,∴
=5时系数为负,∴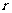 =4,即展开式中系数最大的项为
=4,即展开式中系数最大的项为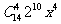 。
。
[巩固]若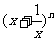 展开式的二项式系数之和为64,则展开式的常数项为( )
展开式的二项式系数之和为64,则展开式的常数项为( )
(07高考重庆理科第4题)
A.10 B.20 C.30 D.120
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com