
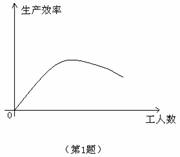
1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.
1.请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
1.3.1单调性与最大(小)值
练习(第32页)
1.3函数的基本性质
5.研究双曲线上一点与两焦点组成的三角形(焦点三角形)问题时,在运用定义的同时还经常用到正、余弦定理。
[举例1] 双曲线 的两焦点为F1、、F2,P在双曲线上,且满足|PF1|+|PF2|=2
的两焦点为F1、、F2,P在双曲线上,且满足|PF1|+|PF2|=2 ,则⊿P F1F2的面积为 ( )
,则⊿P F1F2的面积为 ( )
A. B.1 C.2 D.4
B.1 C.2 D.4
解析:不妨设F1、、F2是双曲线的左右焦点,P为右支上一点,|PF1|-|PF2|=2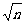 ①
①
|PF1|+|PF2|=2 ②,由①②解得:|PF1|=
②,由①②解得:|PF1|= +
+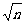 ,|PF2|=
,|PF2|= -
-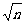 ,得:
,得:
|PF1|2+|PF2|2=4 +4=|F1F2|2,∴PF1⊥PF2,又由①②分别平方后作差得:|PF1||PF2|=2,选B。
+4=|F1F2|2,∴PF1⊥PF2,又由①②分别平方后作差得:|PF1||PF2|=2,选B。
[举例2]等轴双曲线x2-y2=a2,(a>0)上有一点P到中心的距离为3,那么点P到双曲线两个焦点的距离之积等于 。
解析:由“平行四边形对角线的平方和等于四条边的平方和”得:
2(|PF1|2+|PF2|2)=36+4c2,又c2=2 a2,得|PF1|2+|PF2|2=18+4 a2 ①,而||PF1|-|PF2||=2 a ②
由 ①-②2得:|PF1||PF2|=9。
[巩固1] 已知椭圆 与双曲线
与双曲线 (
(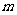 >0,
>0,  >0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=900,则双曲线的离心率为 。
>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=900,则双曲线的离心率为 。
[巩固2] 双曲线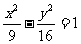 两焦点为F1,F2,点P在双曲线上,直线PF1,PF2倾斜角之差为
两焦点为F1,F2,点P在双曲线上,直线PF1,PF2倾斜角之差为 则△PF1F2面积为:A.16
则△PF1F2面积为:A.16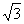 B.32
B.32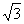 C.32 D.42
C.32 D.42
[提高] 设双曲线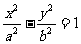 (a,b>0)两焦点为F1、、F2,点P为双曲线右支上除顶点外的任一点,则⊿PF1F2的内心的横坐标为
( )
(a,b>0)两焦点为F1、、F2,点P为双曲线右支上除顶点外的任一点,则⊿PF1F2的内心的横坐标为
( )
A.a B.c C.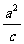 D.与P点的位置有关
D.与P点的位置有关
4.研究双曲线上的点到其焦点的距离问题时,往往用定义;关注定义中的“绝对值”,由此导致一个点在双曲线的左支和右支上的情形是不同的。
[举例1]已知向量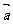 =(
=( ,
, ),
), =(
=( ,-
,- ),双曲线
),双曲线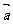 ·
· =1上一点M到F(7,0)的距离为11,N是MF的中点,O为坐标原点,则|ON|=
=1上一点M到F(7,0)的距离为11,N是MF的中点,O为坐标原点,则|ON|=
A. B.
B. C.
C.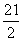 D.
D. 或
或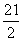
解析:双曲线方程为: ,左支上的点到右焦点F(7,0)的距离的最小值为12,
,左支上的点到右焦点F(7,0)的距离的最小值为12,
∴M是双曲线右支上的点,记左焦点为F/,则|MF/|-|MF|=2a,即|MF/|=21,在⊿MFF/中,ON中位线,∴|ON|=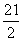 ,故选C。注:本题中,若将M到F(7,0)的距离换为13,将有两种情况(M可能在双曲线的右支上,也可能在左支上)。
,故选C。注:本题中,若将M到F(7,0)的距离换为13,将有两种情况(M可能在双曲线的右支上,也可能在左支上)。
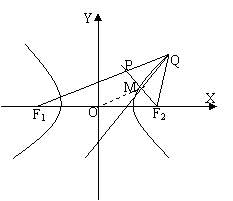 [举例2] 设双曲线
[举例2] 设双曲线 (a,b>0)两焦点
(a,b>0)两焦点
为F1、、F2,点Q为双曲线上除顶点外的任一点,过
焦点F2作∠F1QF2的平分线的垂线,垂足为M,则M
点轨迹是( )
A.椭圆的一部分; B.双曲线的一部分;
C.抛物线的一部分; D.圆的一部分
解析:不妨设Q在双曲线的右支,延长F2M交QF1于P,
在⊿QF1F2中,QM既是角平分线又是高,故|QP|=|QF2|,
又|QF1|-|QF2|=2a,∴|QF1|-|QP|=2a即|PF1|=2a,在⊿PF1F2中,MO是中位线,∴|MO|=a,
∴M点轨迹是圆的一部分,选D。
[巩固1]已知点P在双曲线的左支上, 点M在其右准线上,F1是双曲线的左焦点,且满足:
 ,
,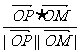 =
= ,则此双曲线的离心率为 。
,则此双曲线的离心率为 。
[巩固2]F1,F2分别为双曲线 (
( >0,
>0, >0)左右焦点,P为双曲线左支上的任意一点,若
>0)左右焦点,P为双曲线左支上的任意一点,若 最小值为8
最小值为8 ,则双曲线的离心率e的取值范围是
。
,则双曲线的离心率e的取值范围是
。
[迁移]P是双曲线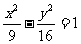 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为
( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为
( )
A.6 B.7 C.8 D.9
3.熟悉双曲线的渐近线的几何特征(无限接近双曲线但与双曲线不相交)和代数特征(渐近线方程是双曲线标准方程中的“1”换为“0”);平行于渐近线的直线与双曲线有且仅有一个交点,但不相切(体现在代数上:直线方程代入曲线方程得到的是一次方程)。已知渐近线方程为: ,则双曲线方程为:
,则双曲线方程为: ,其中
,其中 是待定的参数(渐近线不能唯一地确定双曲线)。双曲线的焦点到渐近线的距离等于半虚轴长b。
是待定的参数(渐近线不能唯一地确定双曲线)。双曲线的焦点到渐近线的距离等于半虚轴长b。
[举例1]双曲线 的一条渐近线与直线
的一条渐近线与直线 垂直,则双曲线的离心率为: A.
垂直,则双曲线的离心率为: A. B.
B. C.
C.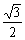 D.
D.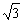 ( )
( )
解析:双曲线 的渐近线方程为:
的渐近线方程为: 即y =±
即y =±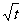 x,(
x,( ≥0)
≥0)
∴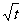 =
= ,双曲线方程为:
,双曲线方程为: ,离心率为
,离心率为  ,选B。
,选B。
[举例2]已知双曲线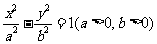 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(A)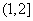 (B)
(B)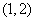 (C)
(C) (D)
(D)
解析:根据双曲线的图形特点知,双曲线渐近线的倾角大于或等于600时,过焦点且倾斜角为600的直线与双曲线的右支有且只有一个交点,于是有 ≥
≥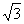
 c2-a2≥3a2,得e≥2。
c2-a2≥3a2,得e≥2。
[巩固1]与双曲线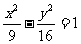 有共同渐近线,且过
有共同渐近线,且过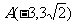 的双曲线的一个焦点到一条渐近线的距离是:( ) A.
的双曲线的一个焦点到一条渐近线的距离是:( ) A. B.
B. C.
C. D.
D.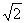
[巩固2]曲线C:x2-y2=1,(x≤0) 上一点P(a,b)到它的一条斜率为正的渐近线的距离为它的离心率,则a+b的值是 ;曲线C的左焦点为F,M(x,y)(y≤0) 是曲线C上的动点,则直线MF的倾角的范围是 .
[迁移]曲线C: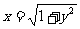 与直线y=kx+1有两个不同的公共点,则k的取值范围是 。
与直线y=kx+1有两个不同的公共点,则k的取值范围是 。
2.双曲线 关于x轴、y轴、原点对称;P(x,y)是双曲线上一点,则|x|≥a,
关于x轴、y轴、原点对称;P(x,y)是双曲线上一点,则|x|≥a,
y∈R,双曲线的焦准距为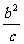 ,双曲线的通经(过焦点且垂直于实轴的弦)长为2
,双曲线的通经(过焦点且垂直于实轴的弦)长为2 ;
;
过焦点的弦中,端点在同一支上时通经最短,端点在两支上时实轴最短。等轴双曲线的离心率为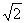 ,渐近线方程为
,渐近线方程为 ;反比例函数
;反比例函数 的图象是一个经过旋转的等轴双曲线,渐近线为两坐标轴,对称轴为直线
的图象是一个经过旋转的等轴双曲线,渐近线为两坐标轴,对称轴为直线 。
。
[举例1] 双曲线 的中心、右焦点、右顶点、右准线与x轴的交点,依次为 O、F、A、H,当|HF|≥
的中心、右焦点、右顶点、右准线与x轴的交点,依次为 O、F、A、H,当|HF|≥ |AF|时,
|AF|时, 的最大值为 。
的最大值为 。
解析:|HF|=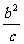 ,|AF|=c-a,∴
,|AF|=c-a,∴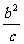 ≥
≥ (c-a)
(c-a)
 ≥
≥
 c≤2a
c≤2a e≤2
e≤2
 =
= =e-
=e-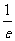 ,记f(e)= e-
,记f(e)= e-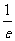 ,函数f(e)在(1,2
,函数f(e)在(1,2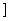 上递增,∴f(e)≤f(2)=
上递增,∴f(e)≤f(2)=
 .
.
[举例2]已知函数 的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹,则这个定长为 .
的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹,则这个定长为 .
解析:双曲线 的实轴所在的直线为y=x,实轴与双曲线的交点即顶点为A1(1,1)和
的实轴所在的直线为y=x,实轴与双曲线的交点即顶点为A1(1,1)和
A2(-1,-1),2a=|A1A2|=2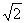 ,此即“定长”。注:我们可以再由等轴双曲线的性质得:c=2,
,此即“定长”。注:我们可以再由等轴双曲线的性质得:c=2,
进而得该双曲线的焦点坐标为(-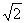 ,-
,-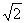 ),(
),(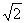 ,
,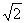 )。
)。
[巩固1] 双曲线 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且
 =0,那么双曲线的离心率为 ( )
=0,那么双曲线的离心率为 ( )
A.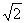 B.
B.
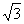 C.2
D.
C.2
D.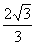
[巩固2] 过双曲线2x2-y2=2的右焦点F的直线交双曲线于A、B两点,若|AB|=4,则这样的直线有 条。
[迁移]已知双曲线 的实轴A1A2,虚轴为B1B2,将坐标系的右半平面沿y轴折起,使双曲线的右焦点F2折至点F,若点F在平面A1
B1B2内的射影恰好是该双曲线左顶点A1,则直线B1F与平面A1 B1B2所成角的正切值为
。
的实轴A1A2,虚轴为B1B2,将坐标系的右半平面沿y轴折起,使双曲线的右焦点F2折至点F,若点F在平面A1
B1B2内的射影恰好是该双曲线左顶点A1,则直线B1F与平面A1 B1B2所成角的正切值为
。
1.方程 表示双曲线
表示双曲线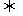
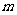
 <0, 双曲线的焦点位置取决于
<0, 双曲线的焦点位置取决于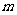 ,
, 的正负:若
的正负:若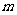 >0,
>0,  <0,双曲线的标准方程是:
<0,双曲线的标准方程是: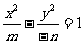 ,a2=
,a2=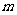 ,b2=-
,b2=- ,焦点在x轴上;若
,焦点在x轴上;若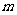 <0,
<0,  >0,双曲线的标准方程是:
>0,双曲线的标准方程是: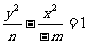 ,a2=
,a2= ,b2=-
,b2=-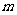 ,焦点在y轴上。
,焦点在y轴上。
[举例]已知 是常数,若双曲线
是常数,若双曲线 的焦距与
的焦距与 的取值无关,则
的取值无关,则 的取值范围是:
( )
的取值范围是:
( )
A.-2< ≤2 B.
≤2 B. >5 C.-2<
>5 C.-2< ≤0 D.0≤
≤0 D.0≤ <2
<2
解析:方程表示双曲线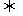 (
( -5)(2-|
-5)(2-| |)<0
|)<0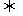 -2<
-2< ≤0或0<
≤0或0< <2或
<2或 >5;当-2<
>5;当-2< ≤0时,方程为:
≤0时,方程为: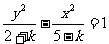 ,a2=2+
,a2=2+ ,b2=5-
,b2=5- ,则c2=7与
,则c2=7与 无关;当0<
无关;当0< <2时,方程为:
<2时,方程为: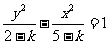 , a2=2-
, a2=2- ,b2=5-
,b2=5- ,则c2=7-2
,则c2=7-2 与
与 有关;当
有关;当 >5时,方程为:
>5时,方程为:
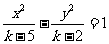 ,a2=
,a2= -5,b2=
-5,b2= -2,则c2=2
-2,则c2=2 -7,与
-7,与 有关;故选C。
有关;故选C。
[巩固1]若 表示焦点在y轴上的双曲线,则它的半焦距c的取值范围是
表示焦点在y轴上的双曲线,则它的半焦距c的取值范围是
。
[巩固2]双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则
A. B.
B. C.
C. D.
D.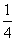
32.读图15,回答下列问题。 (14分)
(1)根据图中信息,说出A、B两条山脉特征的差异。 (6分)
(2)分析图中C处海域及其附近陆地多大雾、阴雨天气的自然原因。 (3分)
(3)2014年的冬奥会将在索契举行。请从地理角度说明索契适宜滑雪比赛的优越自然条件。(2分)
(4)图中D所在国家东部有注入北冰洋的三条大河,试分析这条河流下游农业不发达的自然原因。(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com