
15、(1)因为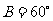 ,所以
,所以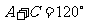 ,
, 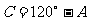 ………………1分
………………1分
因为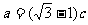 ,由正弦定理可得:
,由正弦定理可得: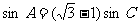 ………………3分
………………3分
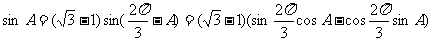
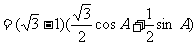 ,整理可得:
,整理可得: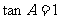 ………………5分
………………5分
所以,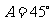 (或
(或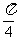 )
………………6分
)
………………6分
(2)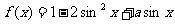 ,令
,令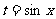 ,因为
,因为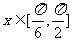 ,所以
,所以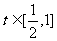 7分
7分
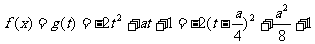 ,
,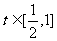 ………………9分
………………9分
若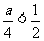 ,即
,即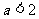 ,
,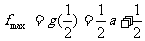 ,
,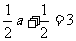 ,则
,则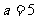 (舍去)…… 10分
(舍去)…… 10分
若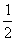
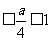 ,即
,即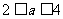 ,
,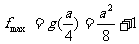 ,
,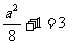 ,得
,得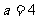 …… 11分
…… 11分
若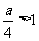 ,即
,即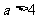 ,
, 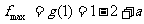
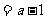 ,
,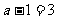 ,得
,得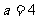 (舍去)12分
(舍去)12分
故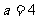 ,
,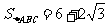 ………………14分
………………14分
8、9;9、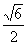 ;10、
;10、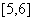 ;11、
;11、 ;12、
;12、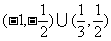 ;13、
;13、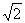 ;14、(1)(4).
;14、(1)(4).
1、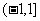 ;2、
;2、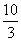 ;3、1;4.1;5、80;6、
;3、1;4.1;5、80;6、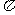 ;7、
;7、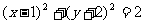 ;
;
16、已知函数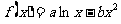 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为 .
.
(Ⅰ)求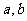 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程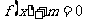 在
在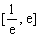 内有两个不等实根,求
内有两个不等实根,求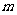 的取值范围(其中
的取值范围(其中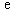 为自然对数的底,
为自然对数的底, );
);
15.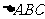 中,三个内角
中,三个内角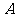 、
、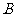 、
、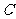 所对的边分别为
所对的边分别为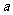 、
、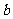 、
、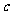 ,若
,若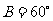 ,
, 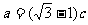 .
.
(1)求角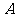 的大小;(2)已知当
的大小;(2)已知当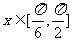 时,函数
时,函数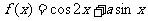 的最大值为3,求
的最大值为3,求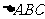 的面积.
的面积.
14.以下有四种说法:(1)若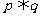 为真,
为真, 为假,则
为假,则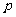 与
与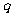 必为一真一假;
必为一真一假;
(2)若数列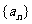 的前
的前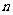 项和为
项和为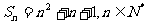 ,则
,则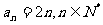 ;
;
(3)若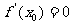 ,则
,则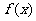 在
在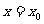 处取得极值;
处取得极值;
(4)由变量x和y的数据得到其回归直线方程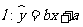 ,则
,则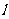 一定经过点
一定经过点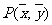 .以上四种说法,其中正确说法的序号为
.
.以上四种说法,其中正确说法的序号为
.
13.已知函数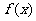 满足,
满足,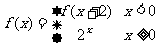 ,则
,则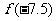 =
.
=
.
12.研究问题:“已知关于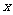 的不等式
的不等式 的解集为
的解集为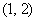 ,解关于
,解关于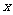 的不等式
的不等式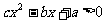 ”,有如下解决方案:
”,有如下解决方案:
 解:由
解:由

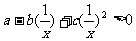 ,令
,令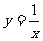 ,则
,则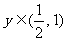 ,
,
所以不等式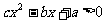 的解集为
的解集为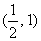 .
.
参考上述解法,已知关于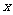 的不等式
的不等式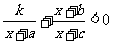 的解集为
的解集为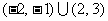 ,
,
则关于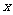 的不等式
的不等式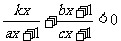 的解集为
.
的解集为
.
11.对于函数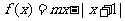 (
(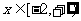 ),若存在闭区间
),若存在闭区间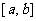
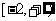
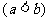 , 使得对任意
, 使得对任意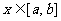 ,恒有
,恒有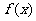 =
=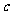 (
(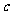 为实常数),则实数
为实常数),则实数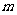 = .
= .
10.函数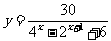 ,
, 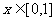 的值域是
.
的值域是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com