
22、(14分)设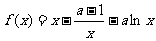
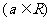 .
.
(1)若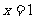 是函数
是函数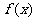 的极大值点,求
的极大值点,求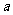 的取值范围;
的取值范围;
(2)当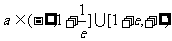 时,若在
时,若在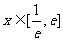 上至少存在一点
上至少存在一点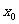 ,使
,使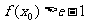 成立,求
成立,求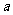 的取值范围.
的取值范围.
21、(15分)点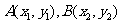 是抛物线
是抛物线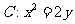 上的不同两点,过
上的不同两点,过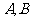 分别作
分别作
抛物线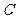 的切线,两条切线交于点
的切线,两条切线交于点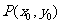 .
.
(1)求证: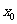 是
是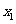 与
与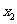 的等差中项;
的等差中项;
(2)若直线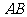 过定点
过定点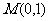 ,求证:原点
,求证:原点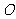 是
是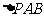 的垂心;
的垂心;
(3)在(2)的条件下,求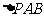 的重心
的重心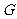 的轨迹方程.
的轨迹方程.
20、(15分)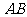 为圆
为圆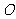 的直径,点
的直径,点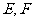
 在圆上,
在圆上,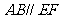 ,矩形
,矩形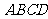 所在
所在
平面与圆 所在平面互相垂直,
所在平面互相垂直,
已知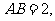
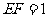 .
.
(1)求证: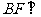 平面
平面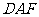 ;
;
(2)求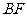 与平面
与平面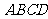 所成的角;
所成的角;
(3)在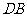 上是否存在一点
上是否存在一点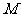 ,
,
使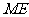
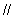 平面
平面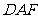 ?若不存在,请说明理由;
?若不存在,请说明理由;
若存在,请找出这一点,并证明之.
19、(14分)袋中装有编号为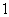 的球
的球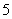 个,编号为
个,编号为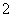 的球
的球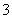 个,这些球的大小完全一样.
个,这些球的大小完全一样.
(1)从中任意取出四个,求剩下的四个球都是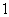 号球的概率;
号球的概率;
(2)从中任意取出三个,记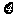 为这三个球的编号之和,
为这三个球的编号之和,
求随机变量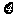 的分布列及其数学期望
的分布列及其数学期望 .
.
18、(14分)已知函数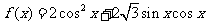 .求
.求
(1)函数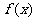 的最小正周期;(2)函数
的最小正周期;(2)函数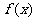 的单调递减区间;
的单调递减区间;
(3)函数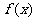 在区间
在区间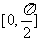 上的最值.
上的最值.
17、整数数列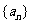 满足
满足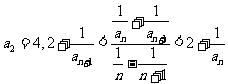 ,则数列
,则数列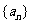 的通项
的通项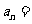 ▲.
▲.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com