
10. 已知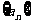 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果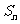 是
是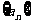 的前n项和,那么
的前n项和,那么
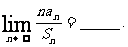
讲解 特别取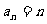 ,有
,有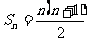 ,于是有
,于是有
 故应填2.
故应填2.
9.设非零复数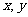 满足
满足 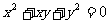 ,则代数式
,则代数式 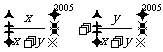 的值是____________.
的值是____________.
讲解 将已知方程变形为 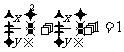 ,
,
解这个一元二次方程,得
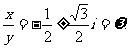
显然有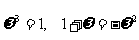 , 而
, 而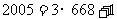 ,于是
,于是
原式=
=
=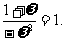
在上述解法中,“两边同除”的手法达到了集中变量的目的,这是减少变元的一个上策,值得重视.
8. 设复数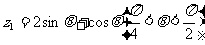 在复平面上对应向量
在复平面上对应向量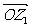 ,
, 将
将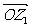 按顺时针方向旋转
按顺时针方向旋转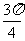 后得到向量
后得到向量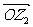 ,
,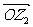 对应的复数为
对应的复数为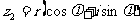 ,则
,则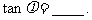
讲解 应用复数乘法的几何意义,得
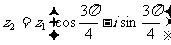
 ,
,
于是 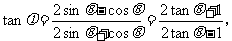
故应填 
7. 如果函数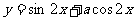 的图象关于直线
的图象关于直线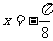 对称,那么
对称,那么
讲解 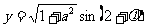 ,其中
,其中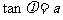 .
.

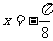 是已知函数的对称轴,
是已知函数的对称轴,
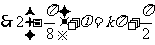 ,
,
即  ,
,
于是  故应填
故应填 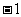 .
.
在解题的过程中,我们用到如下小结论:
函数 和
和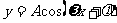 的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
的图象关于过最值点且垂直于x轴的直线分别成轴对称图形.
6. 不等式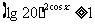 (
( )的解集为
)的解集为 .
.
讲解 注意到 ,于是原不等式可变形为
,于是原不等式可变形为

而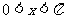 ,所以
,所以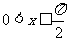 ,故应填
,故应填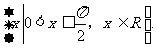
5. 已知点P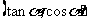 在第三象限,则角
在第三象限,则角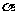 的终边在第
的终边在第 象限.
象限.
讲解 由已知得

从而角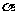 的终边在第二象限,故应填二.
的终边在第二象限,故应填二.
4. 果函数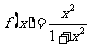 ,那么
,那么
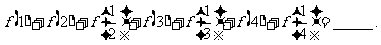
讲解 容易发现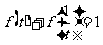 ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式=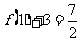 ,应填
,应填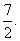
本题是2002年全国高考题,十分有趣的是,2003年上海春考题中也有一道类似题:
设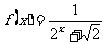 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得
3. 若函数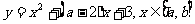 的图象关于直线
的图象关于直线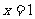 对称,则
对称,则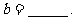
讲解 由已知抛物线的对称轴为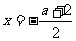 ,得
,得 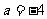 ,而
,而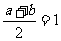 ,有
,有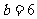 ,故应填6.
,故应填6.
1 已知函数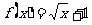 ,则
,则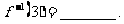
讲解 由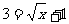 ,得
,得
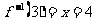 ,应填4.
,应填4.
请思考为什么不必求 呢?
呢?
2. 集合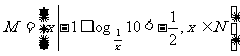 的真子集的个数是
的真子集的个数是
讲解 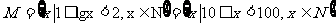 ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是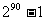 ,应填
,应填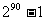 .
.
快速解答此题需要记住小结论;对于含有n个元素的有限集合,其真子集的个数是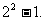
通过“化复杂为简单、化陌生为熟悉”,将问题等价地转化成便于解决的问题,从而得出正确的结果。
例10 不等式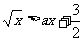 的解集为(4,b),则a=
,b=
。
的解集为(4,b),则a=
,b=
。
解:设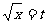 ,则原不等式可转化为:
,则原不等式可转化为: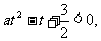 ∴a > 0,且2与
∴a > 0,且2与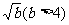 是方程
是方程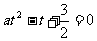 的两根,由此可得:
的两根,由此可得: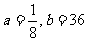 。
。
例11 不论k为何实数,直线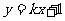 与曲线
与曲线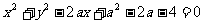 恒有交点,则实数a的取值范围是 。
恒有交点,则实数a的取值范围是 。
解:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆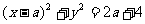 ,∴
,∴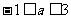 。
。
例12 函数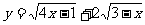 单调递减区间为
。
单调递减区间为
。
解:易知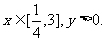 ∵y与y2有相同的单调区间,而
∵y与y2有相同的单调区间,而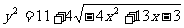 ,∴可得结果为
,∴可得结果为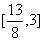 。
。
总之,能够多角度思考问题,灵活选择方法,是快速准确地解数学填空题的关键。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com