
6.设双曲线 (a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于
( )
(a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于
( )
(A)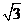 (B)2
(C)
(B)2
(C)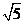 (D)
(D)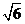
7函数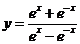 的图像大致为
( ).
的图像大致为
( ).
( A ).
3.已知向量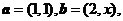 若
若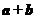 与
与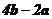 平行,则实数
平行,则实数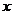 的值是
( )
的值是
( )
A.-2 B.0 C.1 D.2
4将函数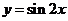 的图象向左平移
的图象向左平移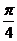 个单位, 再向上平移1个单位,所得图象的函数解析式是
( ).
个单位, 再向上平移1个单位,所得图象的函数解析式是
( ).
A.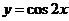 B.
B.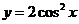 C.
C. D.
D.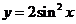
5给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是 ( )
A. ①和② B. ②和③ C. ③和④ D. ②和④
2.设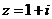 (
(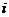 是虚数单位),则
是虚数单位),则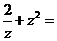 ( )
( )
A.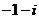 B.
B.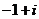 C.
C. D.
D. 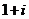
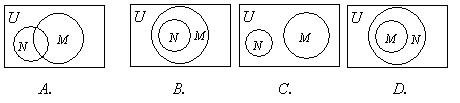
1.已知全集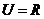 ,则正确表示集合
,则正确表示集合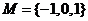 和
和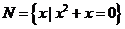 关系的韦恩(Venn)图是 ( )
关系的韦恩(Venn)图是 ( )
22.(本小题满分12分)已知双曲线C的方程为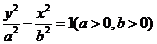 ,离心率
,离心率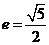 ,
,
顶点到渐近线的距离为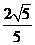 。
求 (1)双曲线C的方程;
。
求 (1)双曲线C的方程;
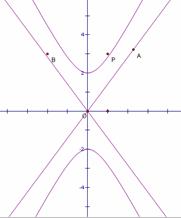 (2)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若
(2)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若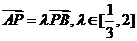 ,求
,求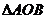 面积的取值范围。
面积的取值范围。
21.(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1.
(Ⅰ)若函数f(x)在x=-2处有极值,求f(x)的表达式;
(Ⅱ)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围.
20.(本小题满分12分)
已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==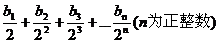 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
19.(本小题满分12分)
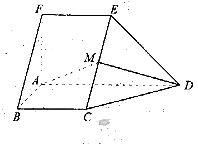 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 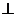 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB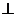 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=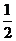 AD
AD
(1) 证明平面AMD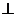 平面CDE;
平面CDE;
(2)求二面角A-CD-E的余弦值。
18.(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是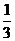 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率; (2)求这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
17.(本小题满分10分)
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量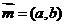 ,
,
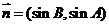 ,
,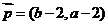 .(1)若
.(1)若 //
//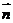 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)若 ⊥
⊥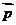 ,边长c = 2,角C =
,边长c = 2,角C = 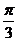 ,求ΔABC的面积 .
,求ΔABC的面积 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com