
18.(本题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为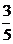 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,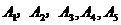 还喜欢打羽毛球,
还喜欢打羽毛球,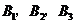 还喜欢打乒乓球,
还喜欢打乒乓球,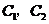 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求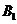 和
和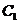 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
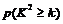 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
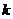 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: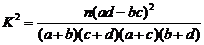 ,其中
,其中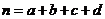 )
)
17. (本题满分14分)
(本题满分14分)
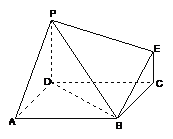
右图为一简单组合体,其底面ABCD为正方形,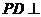 平面
平面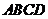 ,
,
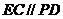 ,且
,且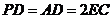 =2 .
=2 .
(1)答题卡指定的方框内已给出了该几何体的俯视图,请在方框
内画出该几何体的正(主)视图和侧(左)视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: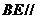 平面
平面 .
.
证明过程和演算步骤.
16.(本题满分12分)
已知复数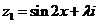 ,
,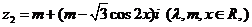 ,且
,且 .
.
(1)若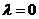 且
且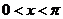 ,求
,求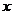 的值;
的值;
(2)设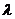 =
=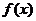 ,求
,求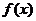 的最小正周期和单调减区间.
的最小正周期和单调减区间.
(二)选做题(14、15题,考生只能从中选做一题)
14.设直线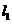 的参数方程为
的参数方程为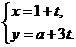 (
(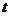 为参数),直线
为参数),直线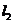 的方程为
的方程为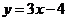 ,若直线
,若直线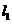 与
与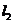 间的距离为
间的距离为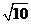 ,则实数
,则实数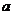 的值为
.
的值为
.
15.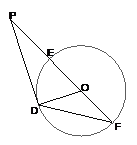 (几何证明选做题)如图,已知
(几何证明选做题)如图,已知 是
是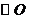 外一点,
外一点,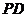 为
为
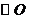 的切线,
的切线,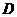 为切点,割线PEF经过圆心
为切点,割线PEF经过圆心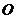 ,若
,若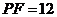 ,
,
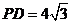 ,则圆
,则圆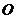 的半径长为
、
的半径长为
、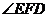 的度
的度
数为 .
(一)必做题(11-13题)
11. 命题“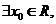
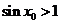 ”的否定为
.
”的否定为
.
12.椭圆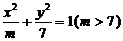 上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为
.
上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项,则P点的坐标为
.
13.随机抽取某中学甲、乙两个班各10名同学,测量他们的身高(单位:cm)获得身高数据的茎叶图如下图甲,在样本的20人中,记身高在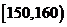 ,
,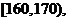
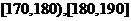 的人数依次为
的人数依次为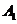 、
、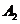 、
、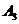 、
、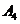 .图乙是统计样本中身高在一定范围内的人数的算法流程图,由图甲可知甲、乙两班中平均身高较高的是 班;图乙输出的
.图乙是统计样本中身高在一定范围内的人数的算法流程图,由图甲可知甲、乙两班中平均身高较高的是 班;图乙输出的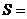 .(用数字作答)
.(用数字作答)
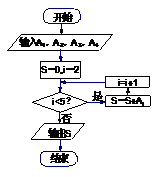

图甲 图乙
10.甲乙两人同时从A地出发往B地,甲在前一半时间以速度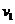 行驶,在后一半时间以速度
行驶,在后一半时间以速度 行驶,乙在前一半路程以速度
行驶,乙在前一半路程以速度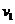 行驶,在后一半路程以速度
行驶,在后一半路程以速度 行驶,(
行驶,( ).则下列说法正确的是
).则下列说法正确的是
A.甲先到达B地 B. 乙先到达B地
C.甲乙同时到达B地 D.无法确定谁先到达B地
9.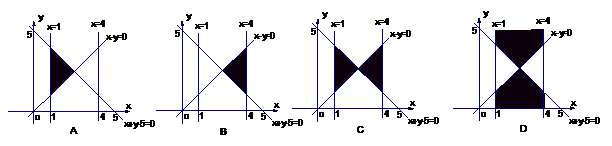 已知函数
已知函数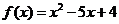 ,则不等式组
,则不等式组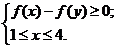 对应的平面区域为
对应的平面区域为
7.若函数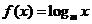 的反函数的图象过点
的反函数的图象过点 ,则
,则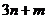 的最小值是A.
的最小值是A.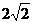 B.2 C.
B.2 C.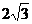 D.
D.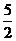 8.已知点O为△ABC外接圆的圆心,且
8.已知点O为△ABC外接圆的圆心,且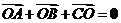 ,则△ABC的内角A等于
,则△ABC的内角A等于
A.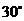 B.
B. C.
C.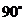 D.
D.
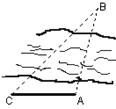
6. 如图,设A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸
边选定一点C,测出AC的距离为50m,∠ ACB=45°,∠CAB=105°后,
就可以计算出A、B两点的距离为
A.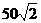 m B.
m B.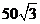 m C.
m C.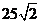 m D.
m D.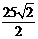 m
m
5.过曲线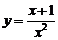 (
(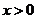 )上横坐标为1的点的切线方程为
)上横坐标为1的点的切线方程为
 A.
A. B.
B. 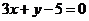 C.
C.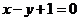 D.
D. 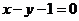
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com