
19.(本小题满分12分)
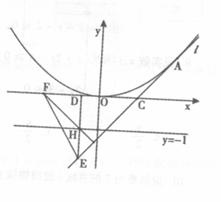
如图,已知抛物线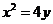 ,过抛物线上一点
,过抛物线上一点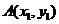 (不同于顶点)作抛物线的切线
(不同于顶点)作抛物线的切线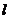 ,并交
,并交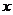 轴于点C,在直线
轴于点C,在直线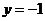 上任取一点H,过H作HD垂直
上任取一点H,过H作HD垂直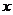 轴于D,并交于
轴于D,并交于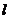 于点E,过H作直线HF垂直直线
于点E,过H作直线HF垂直直线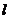 ,并交
,并交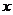 轴于点F。
轴于点F。
(I)
证明: 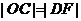 ;
;
(II) 试判断直线EF与抛物线的位置关系并说明理由。
(20)(本小题满分12分)
商场现有某商品1320件,每件成本110元,如果每件售价200元,每天可销售40件.“十一”期间,商场决定降价促销,根据市场信息,单价每降低3元,每天可多销售2件
( I )每件售价多少元,商场销售这一商品每天的利润最大?
(Ⅱ)如果商场决定在这个节日期间15天内售完,在不亏本的前提下,每件售价多少元。商场销售这一商品每天的销售额最大
18.(本小题满分12分)
在1,2,3,…,9这9个自然数中,任取3个数。
(I)2求这3个数中恰有1个是偶数的概率;
(II)设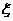 为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时
为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时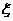 的值是2)。求随机变量
的值是2)。求随机变量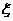 的分布列及其数学期望E
的分布列及其数学期望E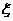 。
。
17.(本小题满分13分)
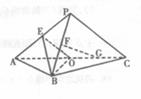
如图,平面PAC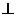 平面ABC,
平面ABC,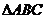 是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10。
是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10。
(I)
设G是OC的中点,证明:FG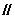 平面BOE;
平面BOE;
(II)
证明:在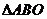 内存在一点M,使FM
内存在一点M,使FM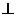 平面BOE,并
平面BOE,并
求点M到OA,OB的距离。
16.(本小题满分12分)
在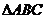 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为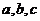 且满足
且满足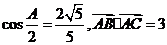 ,
,
(I)
求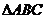 的面积;(II)若
的面积;(II)若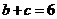 ,求
,求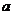 的值。
的值。
15.过点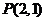 作直线
作直线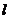 分别交
分别交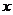 轴
轴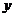 轴的正半周于A、B两点,则
轴的正半周于A、B两点,则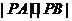 的值最小时直线
的值最小时直线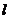 的方程是
。
的方程是
。
14.随机地向半圆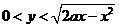 (
(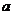 为正常数)
为正常数)
内掷一点,点落在该半圆内任何区域的概率与此区域的
面积成正比,求原点与该点的连线与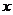 轴的夹角小于
轴的夹角小于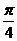 的概率
。
的概率
。
13.已知抛物线C的顶点在坐标原点,焦点为F(1,0)
,直线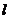 与抛物线C相交于A,B两点,若AB的中点
与抛物线C相交于A,B两点,若AB的中点
为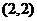 ,则直线
,则直线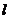 的方程为
。
的方程为
。
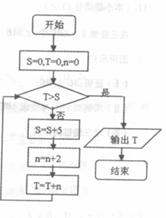
12.执行右边的程序框图,输出的T=
。
11. 若直线
若直线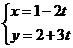 (
(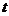 为参数)与直线
为参数)与直线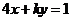 垂直,则常数
垂直,则常数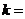 。
。
10.设斜率为2的直线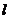 过抛物线
过抛物线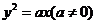 的焦点F,且和
的焦点F,且和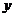 一轴交于点A,若
一轴交于点A,若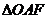 (O为坐标原点)的面积为4,则抛物线方程为
(O为坐标原点)的面积为4,则抛物线方程为
A.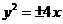 B.
B.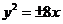 C.
C.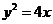 D.
D.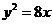
第II卷(非选择题 共100分)
用0.5毫米黑色签字笔在答题卡上书写作答,再试题卷上作答,答案无效。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com