
2010.4
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共300分。考试时间150分钟。考试结束,将本试卷和答题卡一并收回。
第Ⅰ卷(选择题共140分)
本卷共35小题,每小题4分,共140分。在每小题列出的四个选项中。选出最符合题
目要求的一项。
当地时间2月12日18时(区时),第21届冬奥会在温哥华(北纬49°16′,西经123°7′)哥伦比亚体育馆拉开帷幕。温哥华是加拿大西岸最大的港口。回答l、2题。
20.(本小题共14分)
已知数列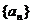 满足
满足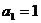 ,点
,点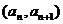 在直线
在直线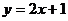 上.
上.
(I)求数列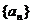 的通项公式;
的通项公式;
(II)若数列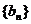 满足
满足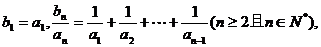
求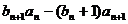 的值;
的值;
(III)对于(II)中的数列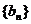 ,求证:
,求证: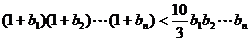
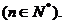
19.(本小题共14分)
已知椭圆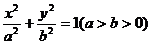 的离心率为
的离心率为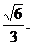
(I)若原点到直线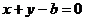 的距离为
的距离为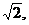 求椭圆的方程;
求椭圆的方程;
(II)设过椭圆的右焦点且倾斜角为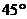 的直线
的直线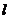 和椭圆交于A,B两点.
和椭圆交于A,B两点.
(i)当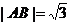 ,求b的值;
,求b的值;
(ii)对于椭圆上任一点M,若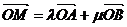 ,求实数
,求实数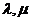 满足的关系式.
满足的关系式.
18.(本小题共13分)
已知函数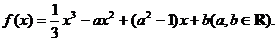
(I)若x=1为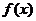 的极值点,求a的值;
的极值点,求a的值;
(II)若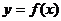 的图象在点(1,
的图象在点(1,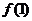 )处的切线方程为
)处的切线方程为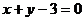 ,
,
(i)求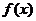 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;
(ii)求函数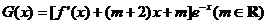 的单调区间.
的单调区间.
17.(本小题共13分)
某公司要将一批海鲜用汽车运往A城,如果能按约定日期送到,则公司可获得销售收入30万元,每提前一天送到,或多获得1万元,每迟到一天送到,将少获得1万元,为保证海鲜新鲜,汽车只能在约定日期的前两天出发,且行驶路线只能选择公路1或公路2中的一条,运费由公司承担,其他信息如表所示.
 统计信息 统计信息汽车行驶 路线 |
不堵车的情况下到达所需时间(天) |
堵车的情况下到达所需时间(天) |
堵车的概率 |
运费(万元) |
|
公路1 |
2 |
3 |
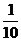 |
1.6 |
|
公路2 |
1 |
4 |
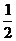 |
0.8 |
(I)记汽车走公路1时公司获得的毛利润为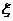 (万元),求
(万元),求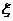 的分布列和数学期望
的分布列和数学期望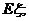
(II)假设你是公司的决策者,你选择哪条公路运送海鲜有可能获得的毛利润更多?
(注:毛利润=销售收入-运费)
16.(本小题共13分)
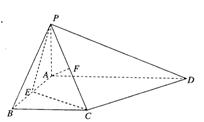
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,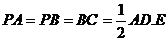 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
 (II)求二面角C-PE-A的余弦值;
(II)求二面角C-PE-A的余弦值;
(III)若四棱锥P-ABCD的体积为4,求AF的长.
15.(本小题共13分)
已知函数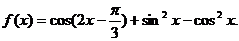
(I)求函数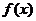 的最小正周期及图象的对称轴方程;
的最小正周期及图象的对称轴方程;
(II)设函数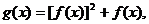 求
求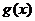 的值域.
的值域.
14.有下列命题:
①若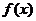 存在导函数,则
存在导函数,则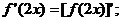
②若函数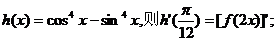
③若函数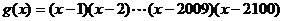 ,则
,则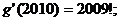
④若三次函数 则
则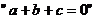 是“
是“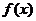 有极值点”的充要条件.
有极值点”的充要条件.
其中真命题的序号是 .
3
13.若A,B,C为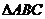 的三个内角,则
的三个内角,则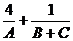 的最小值为
.
的最小值为
.
12.若直线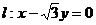 与曲线
与曲线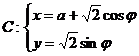
(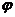 为参数,
为参数,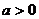 )有两个公共点A,B,且|AB|=2,则实数a的值为
;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为
.
)有两个公共点A,B,且|AB|=2,则实数a的值为
;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com