
63、当空间探测器从行星旁绕过时,由于行星的引力作用,将“偷”取一部分行星的能量,可以使探测器的运动速率增大,这种现象被称之为“弹弓效应”。在航天技术中,“弹弓效应”是用来增大人造小天体运动速率的一种有效方法。1997年10月15日发射升空的卡西尼号宇宙飞船在到达土星前,就是这样“偷’’了两次金星、一次地球的引力使自己加速,直奔土星,当然中途经过巨大的木星更不会放过,照例再“偷”一次。右图就是“弹弓效应”示意图:质量为m的空间探测器以相对于太阳的速度v0飞向质量为M的行星,此时行星相对于太阳的速度u0,探测器绕过行星后相对于太阳的速度为v,,此时行星相对于太阳的速度为u,且m<M,v0、v、u0、u的方向均可视为相互平行。
(1)试写出探测器与行星构成的系统在上述过程中“动量守恒”及“始末状态总动能相等”的方程,并在m<M的条件下,用v0和u0来表示v;
(2)若上述行星是质量为M=5.67×l026kg的土星,其相对于太阳的轨道速率u0=9.6 km/s,而空间探测器的质量m=150 kg,相对于太阳迎向土星的速率v0=10.4 km/s,则由于 “弹弓效应”,该探测器绕过土星后沿与原来速度相反的方向离去,求它离开土星后相对太阳的速率增为多少?
(3)若此探测器飞向行星时其速度v0与土星的速度u0同方向,则是否仍能产生使探测器速率增大的“弹弓效应”,简要说明理由。
解:(1)动量守恒的方程为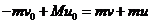 ①
①
始末状态总动能相等的方程为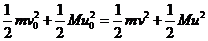 ②
②
解得: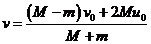 ,当
,当 时,
时,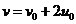 ③
③
(2)代入数据得: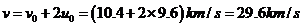
(3)不能。根据如下:
由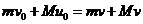 与
与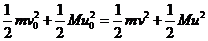 得
得
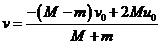 ,故当
,故当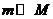 时,
时,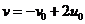 。而
。而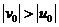 ,故
,故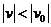 ,不能使探测器速度增大。
,不能使探测器速度增大。
评分标准:(1)(12分)写出①②③两式各得4分;(2)(5分)解出v=29.6km/s,得5分;(3)(5分)判断出不能使探测器速度增大并理由充分得5分,否则酌情扣分。
62、如图所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷量,质量分别为mA和mB.两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与B连接,另一端连接一轻质小钩,整个装置处于方向水平向左的匀强电场中,电场强度为E.开始时A、B静止,已知弹簧的劲度系数为k,不计一切摩擦及A、B间的库仑力,A、B所带电荷量保持不变,B一直在水平面上运动且不会碰到滑轮.试求
(1) 开始A、B静止时,挡板P对物块A的作用力大小;
(2) 若在小钩上挂一质量为M的物块C并由静止释放,当物块C下落到最大距离时物块A对挡板P的压力刚好为零,试求物块C下落的最大距离;
(3) 若C的质量改为2M,则当A刚离开挡板P时,B的速度多大?

解析:(15分)(1)对系统AB:
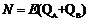 (4分)
(4分)
(2)开始时弹簧形变量为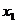 ,由平衡条件:
,由平衡条件: ①(2分)
①(2分)
设当A刚离开档板时弹簧的形变量为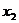 :由:
:由: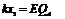 可得
可得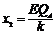 ②(2分)
②(2分)
故C下降的最大距离为: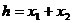 ③……………(1分)
③……………(1分)
由①-③式可解得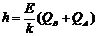 ④…………… (1分)
④…………… (1分)
(3)由能量守恒定律可知:C下落h过程中,C重力势能的的减少量等于B的电势能的增量和弹簧弹性势能的增量以及系统动能的增量之和
当C的质量为M时: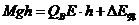 ⑤…(2分)
⑤…(2分)
当C的质量为2M时,设A刚离开挡板时B的速度为V
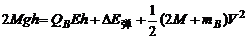 ⑥ …(2分)
⑥ …(2分)
由④-⑥式可解得A刚离开P时B的速度为:
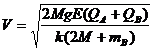 ⑦………………(1分)
⑦………………(1分)
61、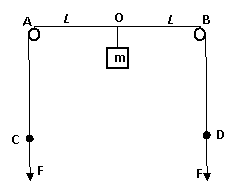 如图所示,轻质长绳水平地跨在相距2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.
如图所示,轻质长绳水平地跨在相距2L的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等,在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.
(1)当物块下落距离h为多大时,物块的加速度为零.
(2)求物块下落过程中的最大速度vm
(3)求物块下落过程中的最大距离H.
(1) h=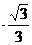 L
(4分)
L
(4分)
(2) Vm= (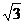 -1 )
-1 ) 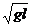 (5分)
(5分)
(3 ) H =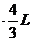 (5分)
(5分)
60、用长为L的细线拉一质量为m的小球,小球带电量为+q,细线一端悬于固定点O,整个装置放在水平向右一足够大的匀强电场中,小球静止时细线与竖直方向的夹角为θ,电场范围足够大,不计空气阻力,重力加速度为g,求:
 (1)匀强电场的电场强度大小;
(1)匀强电场的电场强度大小;
(2)将小球拉至O点正下方最低点由静止释 放,小球向上摆动过程中的最大速度大小;
放,小球向上摆动过程中的最大速度大小;
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是多大?
解:(1)小球静止A点时,受力如图所示
据三力平衡条件,得
tanθ= -------------------------①
E=mgtanθ/q-------------------------②
(2)小球运动到平衡位置时速度最大,由动能定理,得
qELsinθ-mgL(1-cosθ)= mv 2--------------③
2--------------③
将②式代入,得
v=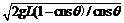 -----------④
-----------④
小球从最底点到最高点时,细线与竖直方向成α角,由动能定理,得
qELsinα-mgL(1-cosα)=0----------------------⑤
将①式代入③式,得
tanθsinα = 1-cosα-------------------⑥
∴ α=2θ---------⑦
在最高点,重力与电场力合力的法线分力与拉力平衡,设线的拉力为F
F= mg
(3)设B点与A点对悬点O对称,即AB为圆轨迹的直径
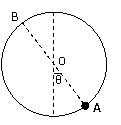 当小球恰好能运动到B点时,就能在竖直面内恰好做完整的圆周运动
当小球恰好能运动到B点时,就能在竖直面内恰好做完整的圆周运动
在B点,重力与电场力的合力提供向心力
mg/cosθ= m-------⑧
设将小球拉至O点正下方最低点时给它一水平向右的初速度为v0,由动能 定理,得
定理,得
-2mgLcosθ-qELsinθ= mvB2- mv02---------------------⑨
将①⑦式代入⑧式,得
v0=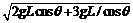 -----------------------------⑩
-----------------------------⑩
59、如图所示,质量M=0.40㎏的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中的虚线区域。当靶盒A进入相互作用区域时便有向左的水平恒力F=20N作用。在P处有一固定的发射器B,它可根据需要瞄准靶盒每次发射一颗水平速度V0=50m/s、质量m=0.10㎏的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短。若每当靶盒A停在或到达O点时,就有一颗子弹进入靶盒A内,求:
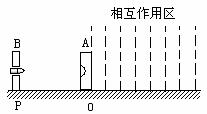 (1)当第一颗子弹进入靶盒A后,靶盒A离开O点的最大距离。
(1)当第一颗子弹进入靶盒A后,靶盒A离开O点的最大距离。
(2)当第三颗子弹进入靶盒A后,靶盒A从离开O点到又回到O点所经历的时间
(3)当第100颗子弹进入靶盒时,靶盒已经在相互作用区中运动的时间和。
(1)设第一颗子弹进入靶盒A后,子弹与靶盒的共内速度为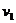 。
。
根据碰撞过程系统动量守恒,有: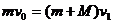 (2分)
(2分)
设A离开O点的最大距离为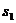 ,由动能定理有:
,由动能定理有: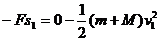 (2分)
(2分)
解得: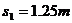 (2分)
(2分)
(2)根据题意,A在的恒力F的作用返回O点时第二颗子弹正好打入,由于A的动量与第二颗子弹动量大小相同,方向相反,故第二颗子弹打入后,A将静止在O点。设第三颗子弹打入A后,它们的共同速度为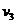 ,由系统动量守恒得:
,由系统动量守恒得: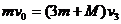 (2分)
(2分)
设A从离开O点到又回到O点所经历的时间为t,取碰后A运动的方向为正方向,由动量定理得: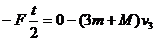 (2分)
(2分)
解得: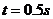 (2分)
(2分)
(3)从第(2)问的计算可以看出,第1、3、5、……(2n+1)颗子弹打入A后,A运动时间均为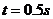 (3分)
(3分)
故总时间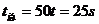 (3分)
(3分)
58、一质量为M的平板小车上,站着n个质量均为m的人,车原来静止在光滑的水平地面上,人相对车静止,现在n个人从车的后端跳下,从车上跳下时,人相对于小车的速度均为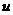 ,试求在下列两种情况下:(1)n个人同时从车的后端跳下后,小车运动的速度多大?(2)车上的人依次都从车的后端跳下,那么当车上的人全都跳下车后,小车运动的速度是多大?
,试求在下列两种情况下:(1)n个人同时从车的后端跳下后,小车运动的速度多大?(2)车上的人依次都从车的后端跳下,那么当车上的人全都跳下车后,小车运动的速度是多大?
解析:(1)以平板小车和n个人为系统,设n个人同时从车上跳下后,小车的速度为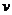 ,根据系统动量守恒,有
,根据系统动量守恒,有 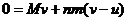 ,解得
,解得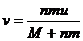
(2)根据动量守恒定律,设第一个人跳下后小车的速度为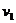 ,于是有
,于是有
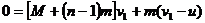 ∴
∴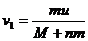
同理,设第二个人跳下后小车的速度为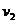 ,于是有
,于是有
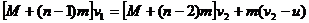 ∴
∴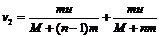
第三个人跳下后小车的速度为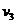 ,于是有
,于是有
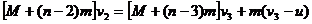
∴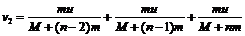
…… ……
第n个人跳下后小车的速度为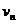 ,于是有
,于是有
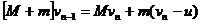
∴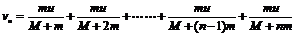
32.[生物--现代生物科技专题](10分)
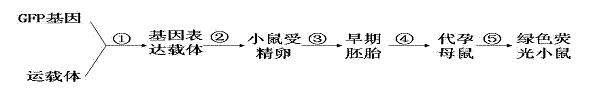 2008年诺贝尔化学奖授予了三位在研究绿色荧光蛋白(GFP)方面做出突出贡献的科学家。绿色荧光蛋白能在蓝光或紫外光的激发下发出荧光,这样借助GFP发出的荧光就可以跟踪蛋白质在细胞内部的移动情况,帮助推断蛋白质的功能。GFP基因可作为目的基因用于培育绿色荧光小鼠,下图表示培育绿色荧光小鼠的基本流程:
2008年诺贝尔化学奖授予了三位在研究绿色荧光蛋白(GFP)方面做出突出贡献的科学家。绿色荧光蛋白能在蓝光或紫外光的激发下发出荧光,这样借助GFP发出的荧光就可以跟踪蛋白质在细胞内部的移动情况,帮助推断蛋白质的功能。GFP基因可作为目的基因用于培育绿色荧光小鼠,下图表示培育绿色荧光小鼠的基本流程:
请根据上述材料回答下列问题:
(1)过程①必需用到的工具酶是 。
(2)过程②将基因表达载体导入小鼠受精卵时,采用最多也最有效的方法是 。然后还可以通过 技术来检测绿色荧光蛋白基因是否已导入成功。
(3)在进行过程④前,利用 技术可以获得数目更多且基因型相同的绿色荧光小鼠。
(4)GFP基因与目的基因一起构建到载体上不影响目的基因的表达,也不影响由目的基因控制合成的蛋白质的结构与功能,且对细胞无毒性作用,因此GFP基因可以运用作为基因表达载体上的 。
福建宁德四县市一中2010届高三第一次联考
31.[化学选考----有机化学](13分)
根据图示填空
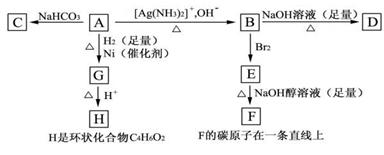
(1)化合物A含有的官能团是_________________________。
(2)B在酸性条件下与Br2反应得到E,E在足量的氢氧化钠醇溶液作用下转变成F,由E转变成F时发生两种反应,其反应类型分别是_____________、____________。
(3)D的结构简式是______________________。
(4)1 mol A与2 mol H2 反应生成1 mol G,其反应方程式是_____________________。
(5)与A具有相同的官能团的A的同分异构体的结构简式是_____________________
30.[化学选考-----物质结构与性质](13分)
纳米技术制成的金属燃料、非金属固体燃料、氢气等已应用到社会生活和高科技领域。
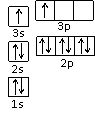 (1)A和B的单质单位质量的燃烧热大,可用作燃料。已知A和B为短周期元素,其原子的第一至第四电离能如下表所示:
(1)A和B的单质单位质量的燃烧热大,可用作燃料。已知A和B为短周期元素,其原子的第一至第四电离能如下表所示:
|
电离能(kJ/mol) |
I1 |
I2 |
I3 |
I4 |
|
A |
932 |
1821 |
15390 |
21771 |
|
B |
738 |
1451 |
7733 |
10540 |
某同学根据上述信息,推断B的核外电子排布如右图所示,该同学所画的核外电子排布式违背了 原理
(2)氢气作为一种清洁能源,必须解决它的储存问题,C60可用作储氢材料。
①已知金刚石中的C-C的键长为154.45pm,C60中C-C键长为145~140pm,有同学据此认为C60的熔点高于金刚石,你认为是否正确并阐述理由 。
②继C60后,科学家又合成了Si60、N60,C、Si、N原子电负性由大到小的顺序是 。
(3)氯化铬酰(CrO2Cl2)在有机合成中可作氧化剂或氯化剂,能与许多有机物反应。请回答下列问题:
①写出铬原子的基态电子排布式_________________________________,与铬同周期的所有元素的基态原子中最外层电子数与铬原子相同的元素有____________(填元素符号)。
②CrO2Cl2常温下为深红色液体,能与CCl4、CS2等互溶,据此可判断CrO2Cl2是__________(填“极性”或“非极性”)分子。
29.[物理选修--3-5](本题有两小题,每小题6分共12分。每小题只有一个选项符合题意。)
(1)下列说法正确的是______
①γ射线在电场和磁场中都不会发生偏转
②β射线比α射线更容易使气体电离
③太阳辐射的能量主要来源于重核裂变
④核反应堆产生的能量来自轻核聚变
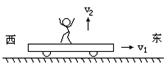 (2)
如图所示,质量为m的人立于平板车上,人与车的总质量为M,人与车以速度v1在光滑水平面上向东运动。当此人相对于车以速度v2竖直跳起时,车向东的速度大小为__________
(2)
如图所示,质量为m的人立于平板车上,人与车的总质量为M,人与车以速度v1在光滑水平面上向东运动。当此人相对于车以速度v2竖直跳起时,车向东的速度大小为__________
①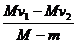 ②
②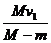 ③
③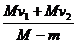 ④V1
④V1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com