
3、已知双曲线过点M(-2,4),N(4,4),它的一个焦点为F1(1,0),则另一个焦点F2的轨迹方程是
(A)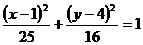 (y≠0)或x=1(y≠0)
(y≠0)或x=1(y≠0)
(B)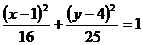 (x≠0)或x=1(y≠0)
(x≠0)或x=1(y≠0)
(C)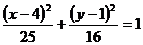 (y≠0)或y=1(x≠0)
(y≠0)或y=1(x≠0)
(D)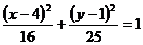 (x≠0)或y=1(x≠0)
(x≠0)或y=1(x≠0)
2、已知函数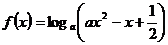 在[1,2]上恒正,则实数a的取值范围是
在[1,2]上恒正,则实数a的取值范围是
(A)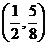 (B)
(B)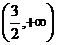
(C)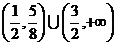 (D)
(D)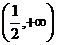
1、在复平面上,非零复数z1、z2在以i对应的点为圆心,1为半径的圆上,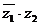 的实部为零,argz1=
的实部为零,argz1=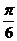 ,则z2=
,则z2=
(A)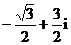 (B)
(B)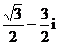
(C)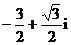 (D)
(D)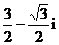
我们称A1,A2,…,An为集合A的一个n分划,如果
(1)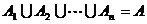 ;
;
(2)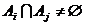 ,1≤i<j≤n.
,1≤i<j≤n.
求最小正整数m,使得对A={1,2,…,m}的任意一个13分划A1,A2,…,A13,一定存在某个集合Ai(1≤i≤13),在Ai中有两个元素a、b满足b<a≤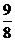 b.
b.
给定由正整数组成的数列
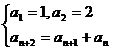 (n≥1).
(n≥1).
(1)求证:数列相邻项组成的无穷个整点
(a1,a2),(a3,a4),…,(a2k-1,a2k),…
均在曲线x2+xy-y2+1=0上.
(2)若设f(x)=xn+xn-1-anx-an-1,g(x)=x2-x-1,证明:g(x)整除f(x).
设ABCD是面积为2的长方形,P为边CD上的一点,Q为△PAB的内切圆与边AB的切点.乘积PA·PB的值随着长方形ABCD及点P的变化而变化,当PA·PB取最小值时,
(1)证明:AB≥2BC;
(2)求AQ·BQ的值.
对正实数a、b、c.求证:
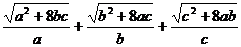 ≥9.
≥9.
第二试
单位正方体ABCD-A1B1C1D1中,正方形ABCD的中心为点M,正方形A1B1C1D1的中心为点N,连AN、B1M.
(1)求证:AN、B1M为异面直线;
(2)求出AN与B1M的夹角.
已知抛物线y2=2px(p>0)的一条长为l的弦AB.求AB中点M到y轴的最短距离,并求出此时点M的坐标.
6、圆周上有100个等分点,以这些点为顶点组成的钝角三角形的个数为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com