
10.解:设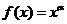 ,则
,则 ,得
,得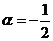 ,
,
即该函数的解析式为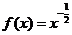 ,
,
该函数的定义域为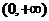 ,定义域不是关于原点对称的,
,定义域不是关于原点对称的,
得该函数是非奇非偶函数,
该函数在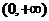 上是递减的.
上是递减的.
B组
10.已知幂函数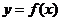 的图象过点
的图象过点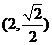 ,试求出此函数的解析式,并作出图象,
,试求出此函数的解析式,并作出图象,
判断奇偶性、单调性.
9.解:(1)设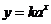 ,当
,当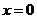 时,
时,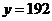 ,即
,即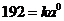 ,得
,得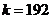 ,
,
当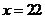 时,
时, ,即
,即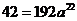 ,
,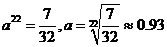 ,
,
得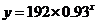 ;
;
(2)当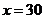 时,
时,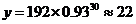 ,
,
当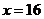 时,
时,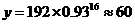 .
.
9.牛奶保鲜时间因储藏时温度的不同而不同,假定保鲜时间与储藏温度间的关系为指数型
函数.若牛奶放在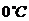 的冰箱中,保鲜时间约是
的冰箱中,保鲜时间约是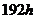 ,而在
,而在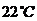 的厨房中则约是
的厨房中则约是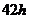 .
.
(1)写出保鲜时间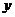 (单位:
(单位: )关于储藏温度
)关于储藏温度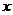 (单位:
(单位: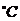 )的函数解析式;
)的函数解析式;
(2)利用(1)中结论,指出温度在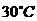 和
和 的保鲜时间(精确到
的保鲜时间(精确到 );
);
(3)运用上面的数据,作此函数的图象.
8.证明:由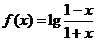 ,得
,得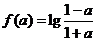 ,
,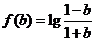 ,
,
而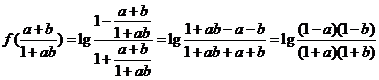 ,
,
因为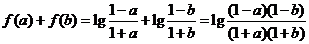 ,
,
所以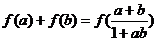 .
.
8. 已知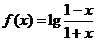 ,
, ,求证:
,求证: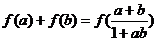 .
.
7.证明:(1)由 ,得
,得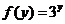 ,
,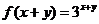 ,
,
因为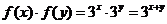 ,
,
所以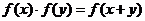 ;
;
(2)由 ,得
,得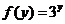 ,
,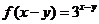 ,
,
因为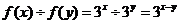 ,
,
所以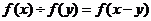 .
.
7.已知 ,求证:
,求证:
(1)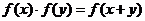 ;(2)
;(2)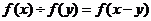 .
.
6.解:(1)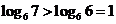 ,即
,即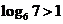 ,
,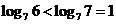 ,即
,即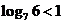 ,
,
得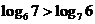 ;
;
(2)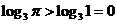 ,即
,即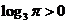 ,
,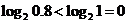 ,即
,即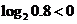 ,
,
得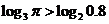 .
.
6.比较下列各组中两个值的大小:
(1)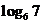 ,
,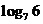 ;(2)
;(2)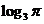 ,
,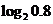 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com