28．已知抛物线y=ax ²+bx+c与x轴交于A、B两点．与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长(OB＜OC)是方程x ²－10x+16=

0的两个根，且抛物线的对称轴是直线x=－2．

　　 (1)求A、B、C三点的坐标；

　　 (2)求此抛物线的表达式；

　　 (3)连接AC、BC，若点E是线段AB上的一个动点(与点A、点B不重合)，过点E作

EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

(4)在(3)的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

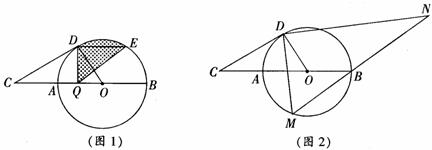
27．如图，AB是⊙O的直径，点C是BA延长线上一点，CD切⊙O于点D，CA=1，CD是⊙O半径的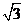倍．

　　 (1)求⊙O的半径R；

　　 (2)如图1，弦DE∥CB，动点Q从A出发沿直径AB向B运动的过程中，图中阴影部分的面积是否发生变化，若发生变化，请你说明理由；若不发生变化，请你求出阴影部分的面积；

(3)如图2，动点M从A出发，在⊙O上按逆时针方向向B运动．连结DM，过D作DM的垂线，与MB的延长线交于点N，当点M运动到什么位置时，DN取到最大值?求此时动点M所经过的弧长．

(本题满分10分)

26．如图，抛物线y=－x ² +2x+3与x轴交于A、B两点，与y轴于点C，点D为对称轴

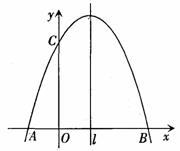
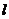上的一个动点．

　　 (1)求当AD+CD最小时，点D的坐标；

　　 (2)以点A为圆心，以AD为半径作⊙A

　　　 ①证明：当AD+CD最小时，直线BD与⊙A相切．

②写出直线BD与⊙A相切时，D点的另一个坐标

_____________．

(本题满分10分)

25．一只不透明的袋子中，装有3个白球和1个红球，这些球除颜色外都相同．

　　 (1)小明认为，搅匀后从中任意摸出一个球，不是白球就是红球，因此摸出白球和摸出红球是等可能的，你同意他的说法吗?为什么?

　　 (2)搅匀后从中摸出两个球，请通过列表或树状图求两球都是白球的概率．

(3)搅匀后从中摸出一个球，要使摸到红球的概率为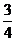，应往袋中添加多少个红球?

24．已知关于x的一元二次方程x ²－x+2m－2=0的两个实根为x ₁，x ₂．

(1)求实数m的取值范围；

(2)如果x ₁、x₂满足x ₁ +2x₂=m+1，求实数m的值．

(本大题共2小题，每小题8分，满分16分)

23．某风景区对5个旅游景点的门票价格进行了调整，根据统计，调价前后各景点的游客人数基本不变，有关数据如下表所示：

　　 (1)该风景区称调整前后这5个景点门票的平均收费不变，平均收入持平，问风景点是怎样计算的．

　　 (2)游客认为调整收费后风景区的平均日收入较调整前实际增加了近13%，问游客是怎样计算的．

　　 (3)你认为谁的说法更切合实际情况．

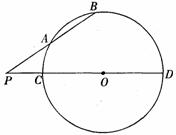
22．如图，已知⊙O的割线PAB交⊙O于A、B两点，PO与⊙O交于C、D两点，且

PA=3cm，PC=2cm，若⊙O的半径为5cm．

(1)PB=__________cm；

(2)求圆心O到AB的距离．

(本大题共2小题，每小题8分，满分16分)

21．已知抛物线y=x ² +(2m+1)x+m+1，根据下列条件分别求m的值．

　 (1)若抛物线过原点；

　　 (2)若抛物线的对称轴为x=1；

　　 (3)若抛物线的顶点在x轴上．

20．解方程：x ²－6x－2=0

(本大题共2小题，每小题6分，满分12分)