
21.(本小题满分12分)
已知函数g(x)=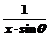 +lnx在[1,+∞)上为增函数,且
+lnx在[1,+∞)上为增函数,且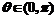 ,
,
f(x)=mx-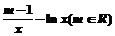
(1)求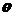 的值;
的值;
(2)若f(x)-g(x)在[1,+∞)上为单调递增函数,求m的取值范围;
(3)设h(x)=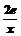 (m>0),若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围。
(m>0),若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围。
20.(本小题满分12分)
抛物线y2=4x的焦点为F,A(x1,y1),B(x2,y2)(x1>x2,y1>0,y2<0)在抛物线上,且存在实数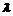 ,使
,使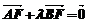 ,|
,|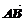 |=
|=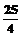
(1)求直线AB的方程; (2)求△AOB的外接圆的方程。
18.(本小题满分12分)
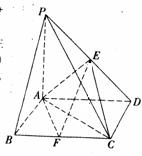
在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,
PB=2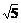 ,PD=4
,PD=4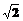 ,E是PD的中点
,E是PD的中点
(1)求证:AE⊥平面PCD;
(2)若F是线段BC的中点,求三棱锥F-ACE的体积。
 19.(本小题满分12分)
19.(本小题满分12分)
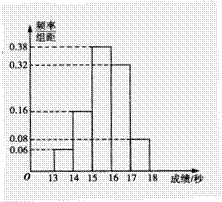
某班50名学生在一次百米测试中,成绩全部介于
13秒与18秒之间,将测试结果按如下方式分成五组:
第一组[13,14),第二组[14,15)……第五组[17,18],
如图是按上述分组方法得到的频率分布直方图
(1)若成绩大于或等于14秒且小于16秒的认为良好,
求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两名同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m-n|>1”的概率。
17.(本小题满分12分)
已知向量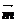 =(sin2x,cosx),
=(sin2x,cosx),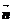 =(
=(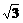 ,2cosx)(x∈R),f(x)=
,2cosx)(x∈R),f(x)=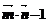
(1)求f(x)的单调递增区间;
 (2)在△ABC中,角A、B、C的对边分别为a,b,c,f(A)=2,a=
(2)在△ABC中,角A、B、C的对边分别为a,b,c,f(A)=2,a=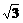 ,B=
,B=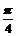 ,求b的值。
,求b的值。
16.已知椭圆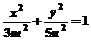 和双曲线
和双曲线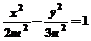 有公共的焦点,则双曲线的渐近线方程为___________________。
有公共的焦点,则双曲线的渐近线方程为___________________。
15.已知三个不同的平面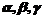 ,a,b,c分别为平面
,a,b,c分别为平面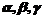 内的直线,若
内的直线,若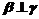 且
且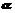 与
与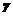 相交但不垂直,则下列命题为真命题的是_________。
相交但不垂直,则下列命题为真命题的是_________。
①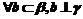 ②
②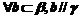 ③
③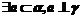
④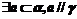 ⑤
⑤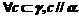 ⑥
⑥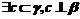
14.将全体正整数排成一个三角形数阵
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … … … … … …
根据以上排列规律,数阵中第n(n≥3)行的从左至右的第3个数是_______。
13.已知向量 =(sin
=(sin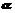 ,2)与向量
,2)与向量 =(cos
=(cos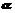 ,1)互相平行,则tan2
,1)互相平行,则tan2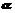 的值为_______。
的值为_______。
12.若f(a)=(3m-1)a+b-2m,当m∈[0,1]时,f(a)≤1恒成立,则a+b的最大值为( )
A.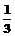 B.
B.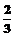 C.
C.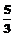 D.
D.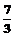
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须做答.第22题-第24题为选考题,考生根据要求做答.
11.若函数y=f(x)(x∈R)满足f(x+2)=f(x)且x∈(-1,1]时f(x)=1-x2,函数g(x)=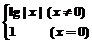 ,则函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为( )
A.12 B.14 C.13 D.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com