
22. 选修4-1:几何证明选讲(本小题10分)
选修4-1:几何证明选讲(本小题10分)
如图,
 ABC内接于⊙O,AB⊥CD于D,E在⊙O上,AE交CD于G,求证:AC2=AG·AE.
ABC内接于⊙O,AB⊥CD于D,E在⊙O上,AE交CD于G,求证:AC2=AG·AE.
21.(本小题满分12分)
已知函数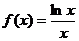 ,
,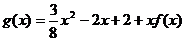 .
.
(Ⅰ)求函数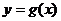 的单调区间;
的单调区间;
(Ⅱ)若函数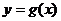 在[
在[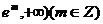 上有零点,求m的最大值;
上有零点,求m的最大值;
选考题:(本小题满分10分)
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.
20.(本小题满分12分)
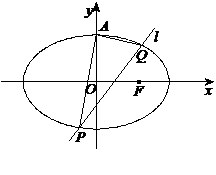 如图,已知椭圆
如图,已知椭圆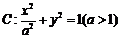 的上顶点为
的上顶点为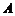 ,右焦点为
,右焦点为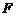 ,直线
,直线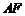 与圆
与圆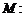
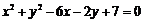 相切.
相切.
(Ⅰ)求椭圆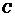 的方程;
的方程;
(Ⅱ)若不过点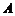 的动直线
的动直线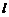 与椭圆
与椭圆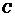 相
相
交于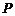 、
、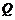 两点,且
两点,且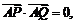 求证:直
求证:直
线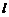 过定点,并求出该定点
过定点,并求出该定点 的坐标.
的坐标.
19.(本小题满分12分)
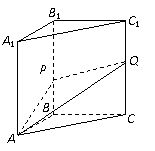
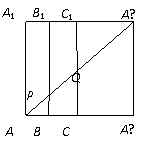
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC-A1B1C1,在三棱柱ABC-A1B1C1中,
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比;
(Ⅲ)求面PQA与面ABC所成的锐二面角的余弦值.
18.(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
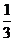 |
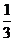 |
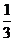 |
概率 |
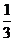 |
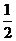 |
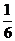 |
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为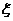 ,求
,求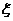 的分布列和期望.
的分布列和期望.
17.(本题满分12分)在ΔABC中,角A、B、C所对的边分别为a、b、c,且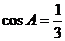 .
.
若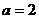 ,
,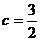 ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.
16.如图三同心圆, 其半径分别为3、2、1. 已知图中阴 影区域的面积是非阴影区域面积的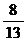 . 则两直线所夹锐角的弧度为
.
. 则两直线所夹锐角的弧度为
.

15.已知x、y满足约束条件 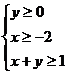 ,则z=(x+3)2+y2的最小值为 .
,则z=(x+3)2+y2的最小值为 .
14.已知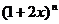 的展开式中,所有项的系数之 和等于81,那么这个展开式中
的展开式中,所有项的系数之 和等于81,那么这个展开式中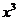 的系数是__________.
的系数是__________.
13.为了了解高三学生的身体状况.抽取了部分
男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12.则抽取的男生人数是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com