
0.015×10×100=15,所以该商业集团A类型连锁店共有25家,D类型连锁店共有15家.
所以i∈{1,2,3,…,25},j∈{1,2,3,…,15}. (7分)
若i+j≥35,则20≤i≤25,j≤15.
当i=20时,j=15,有1种抽取方法;
当i=21时,j=14,15,有2种抽取方法;
当i=22时,j=13,14,15,有3种抽取方法;
当i=23时,j=12,13,14,15,有4种抽取方法;
当i=24时,j=11,12,13,14,15,有5种抽取方法;
当i=25时,j=10,11,12,13,14,15,有6种抽取方法.
记“i+j≥35”为事件A,则事件A包含的基本事件数为1+2+3+4+5+6=21. (10分)
又从A,D两类型连锁店中各随机抽取1家的方法总数为25×15=375.
所以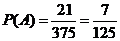 ,故i+j≥35的概率是
,故i+j≥35的概率是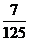 .
(12分)
.
(12分)
17.(本题满分12分)
2009年底,某商业集团根据相关评分标准,对所属100家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A、B、C、D四个类型,其考核评估标准如下表:
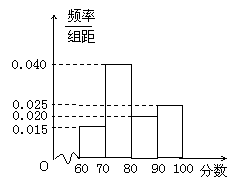 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)估计该商业集团各连锁店评估得分的中位数;
(Ⅱ)假设该商业集团所有商业连锁店的评估得分互不相同,
将所有A类型连锁店按评估得分从高到低依次编号为
A1,A2,A3,…;所有D类型连锁店按评估得分从高
到低依次编号为D1,D2,D3,…,现从A、D两类型
连锁店中各随机抽取1家对各项评估指标进行比较分
析,记被抽取的两家连锁店分别为Ai,Dj,求i+j≥35
的概率.
[解](Ⅰ)因为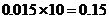 ,
,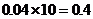 ,在频率分布直方图中,中位数左边和右边的面积相等,所以中位数在区间[70,80)内.
(2分)
,在频率分布直方图中,中位数左边和右边的面积相等,所以中位数在区间[70,80)内.
(2分)
设中位数为70+x,则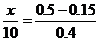 ,解得x=8.75.
(4分)
,解得x=8.75.
(4分)
估计该商业集团各连锁店评估得分的中位数是78.75分. (5分)
(Ⅱ)由直方图可知,A类型连锁店的频数是0.025×10×100=25,D类型连锁店的频数是
16.(本题满分12分)
设锐角△ABC的三内角A,B,C的对边分别为 a,b,c,向量m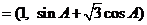 ,n
,n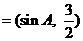 ,已知m与n共线.
,已知m与n共线.
(Ⅰ)求角A的大小;
(Ⅱ)若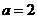 ,
,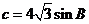 ,且△ABC的面积小于
,且△ABC的面积小于 ,求角B的取值范围.
,求角B的取值范围.
[解](Ⅰ)因为m∥n,则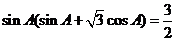 ,即
,即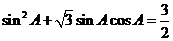 .(2分)
.(2分)
所以 ,即
,即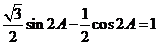 ,即
,即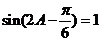 .
(5分)
.
(5分)
A是锐角,则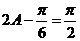 ,所以
,所以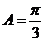 .
(6分)
.
(6分)
(Ⅱ)因为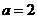 ,
,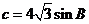 ,则
,则
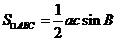
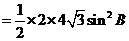
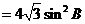
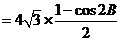
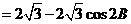 .
(8分)
.
(8分)
由已知,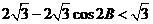 ,即
,即 .
(10分)
.
(10分)
因为B是锐角,所以 ,即
,即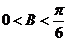 ,故角B的取值范围是
,故角B的取值范围是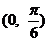 . (12分)
. (12分)
15.对于等差数列{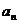 },有如下一个真命题:“若{
},有如下一个真命题:“若{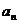 }是等差数列,且
}是等差数列,且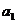 =0,s、t是互不相等的正整数,则
=0,s、t是互不相等的正整数,则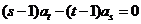 ”.类比此命题,对于等比数列{
”.类比此命题,对于等比数列{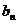 },有如下一个真命题:
},有如下一个真命题:
若{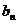 }是等比数列,且
}是等比数列,且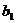 = 1 ,s、t是互不相等的正整数,则
= 1 ,s、t是互不相等的正整数,则 .
.
[解析]设等比数列{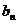 }的公比为q,若
}的公比为q,若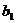 =1,则
=1,则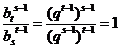 .
.
14.已知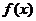 是定义在R上的偶函数,
是定义在R上的偶函数,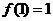 ,且对任意
,且对任意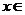 R都有
R都有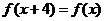 ,则
,则
 1_
.
1_
.
[解析]由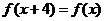 知,
知,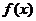 是周期为4的周期函数.
是周期为4的周期函数.
所以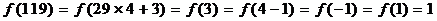 .
.
13.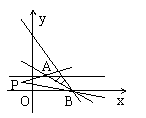 设不等式组
设不等式组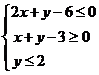 表示的平面区域为M,若函数
表示的平面区域为M,若函数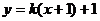 的图象经过区域M,则实数k的取值范围是
的图象经过区域M,则实数k的取值范围是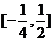 .
.
[解析]作可行域,如图.
因为函数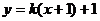 的图象是过点P(-1,1),且斜率为k的直线l,由图知,当直线l过点A(1,2)时,k取最大值
的图象是过点P(-1,1),且斜率为k的直线l,由图知,当直线l过点A(1,2)时,k取最大值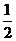 ,当直线l过点B(3,0)时,k取最小值
,当直线l过点B(3,0)时,k取最小值 ,故
,故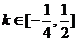 .
.
12.已知圆C的极坐标方程为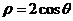 ,直线l的极坐标方程为
,直线l的极坐标方程为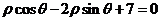 ,则圆心C到直线l的距离是
,则圆心C到直线l的距离是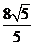 .
.
[解析]圆C的直角坐标方程是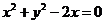 ,直线l的直角坐标方程是
,直线l的直角坐标方程是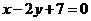 .
.
所以圆心C(1,0)到直线l的距离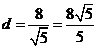 .
.
11.函数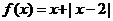 的值域是 [2,+∞) .
的值域是 [2,+∞) .
[解析]因为当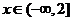 时,
时,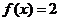 ;当
;当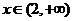 时,
时,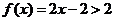 ,故
,故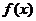 的值域是[2,+∞).
的值域是[2,+∞).
9.不等式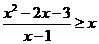 的解集为 [-3,1) .
的解集为 [-3,1) .
[解析]不等式化为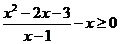 ,即
,即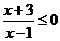 ,所以
,所以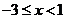 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com