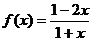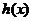3．设函数的反函数为，又函数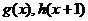的图象关于直线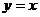对称，，那么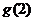的值为 (　　　 )

　 A．-1　　　　　　　 B.-2　　　　　　　　　　 C.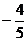　　　　　　 D.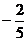

2．方程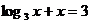的解所在区间是(　　　 )

　A．(0，2)　　　　 B。(1，2)　　　　　　 C.(2，3)　　　 　D.(3，4)

1.函数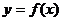与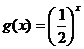的图象关于直线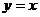对称，则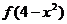的单调递增区间是(　　　 )

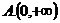
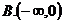
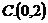
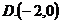
2.不等式恒成立问题要注意等价转化.

冲刺强化训练(2)

　班级　　　　 姓名　　　　 学号　　　　 日期　　 月　　 日　

1.函数不等式的求解要注意结合函数的单调性,特别要重视定义域的作用

例1．设函数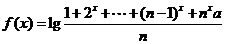，其中a是实数，n是自然数，且n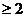，若f(x)当x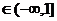时有意义，求a的取值范围。

例2．设函数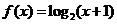，当点(x，y)在y=f(x)的反函数图象上运动时，对应的点(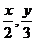)在y=g(x)的图象上。

(1).求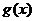的表达式。

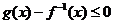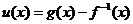(2).当时，求的最小值。

例3．定义在R上的单调函数f(x)满足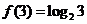且对任意x，y∈R都有f(x+y)=f(x)+f(y)．

(1)求证f(x)为奇函数；

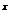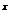(2)若f(k·3)+f(3-9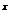-2)＜0对任意x∈R恒成立，求实数k的取值范围．

4．已知f(x)=8+2x-x²，如果g(x)=f(2-x²)，那么g(x)(　　 )

(A)在区间(-2，0)上是增函数。　　　　　　 (B)在区间(0，2)上是增函数。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(C)在区间(-1，0)上是减函数。　　　　　　 (D)在区间(0，1)上是减函数。

3．已知函数f(x)是定义在R上的奇函数，且对一切x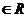，总有f(x+4)=f(x)，

若f(63)=2，则f(5)与f(7)的大小关系是 -------------------

2．若定义在R上的偶函数f(x)在(-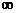，0)上是减函数，且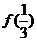=2。那么不等式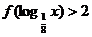的解集为　　　　　　　　　　　　　　　　　　　　 　　(　　 　　　)

(A)(0.5，1)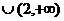　　　　　　　　 (B)(0，0.5)。

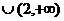(C)(0，0.5)　　　　　　　　　　　　 (D)(2，+)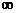

1．函数y=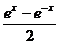的反函数　　　　　　　　　　　　　　　　　　　 (　 　　　　)

A.　　　 是奇函数，它在(0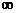，+)上是减函数。

B.　　　 是偶函数，它在(0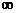，+)上是减函数。

C.　　　 是奇函数，它在(0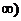，+上是增函数。

D.　　　 是偶函数，它在(0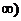，+上是增函数。