
2.对于两个命题:
①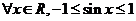 , ②
, ②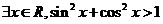 ,
,
下列判断正确的是( )。
A. ① 假 ② 真 B. ① 真 ② 假 C. ① ② 都假 D. ① ② 都真
1.设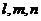 均为直线,其中
均为直线,其中 在平面
在平面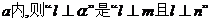 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
22.(本小题满分10分)已知函数
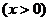 在
在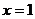 处取得极值
处取得极值 ,其中
,其中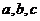 为常数.
为常数.
(1)求 的值;
的值;
(2)讨论函数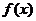 的单调区间;
的单调区间;
(3)若对任意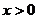 ,不等式
,不等式 恒成立,求
恒成立,求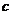 的取值范围.
的取值范围.
21.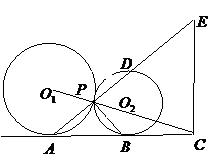 (本小题满分9分)如图,已知⊙
(本小题满分9分)如图,已知⊙ 与⊙
与⊙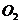 外
外
切于点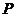 ,
, 是两圆的外公切线,
是两圆的外公切线,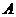 ,
, 为切
为切
点, 与
与 的延长线相交于点
的延长线相交于点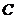 ,延长
,延长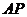
交⊙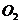 于
点
于
点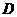 ,点
,点 在
在 延长线上.
延长线上.
(1)求证: 是直角三角形;
是直角三角形;
(2)若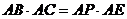 ,试判断
,试判断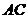 与
与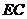 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.
(3)在(2)的条件下,若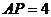 ,
,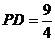 ,求
,求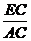 的值.
的值.
20.(本小题满分9分)设在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片,标号分别记为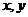 ,设随机变量
,设随机变量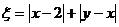 .
.
(1)写出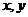 的可能取值,并求随机变量
的可能取值,并求随机变量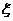 的最大值;
的最大值;
(2)求事件“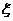 取得最大值”的概率;
取得最大值”的概率;
(3)求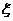 的分布列和数学期望与方差.
的分布列和数学期望与方差.
19.(本小题满分10分)经过点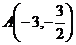 ,倾斜角为
,倾斜角为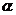 的直线
的直线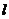 ,与曲线
,与曲线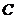 :
: (
( 为参数)相交于
为参数)相交于 两点.
两点.
(1)写出直线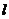 的参数方程,并求当
的参数方程,并求当 时弦
时弦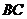 的长;
的长;
(2)当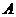 恰为
恰为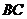 的中点时,求直线
的中点时,求直线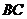 的方程;
的方程;
(3)当 时,求直线
时,求直线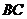 的方程;
的方程;
(4)当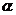 变化时,求弦
变化时,求弦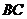 的中点的轨迹方程.
的中点的轨迹方程.
18.(本小题满分10分)设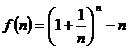 ,其中
,其中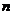 为正整数.
为正整数.
(1)求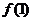 ,
,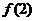 ,
,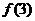 的值;
的值;
(2)猜想满足不等式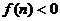 的正整数
的正整数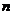 的范围,并用数学归纳法证明你的猜想.
的范围,并用数学归纳法证明你的猜想.
17.(本小题满分8分)设函数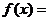
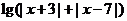
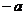 .
.
(1)当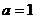 时,解关于
时,解关于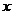 的不等式
的不等式 ;
;
(2)如果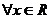 ,
, ,求
,求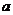 的取值范围.
的取值范围.
16.已知函数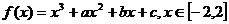 表示过原点的曲线,且在
表示过原点的曲线,且在 处的切线的倾斜角均为
处的切线的倾斜角均为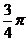 ,有以下命题:
,有以下命题:
①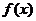 的解析式为
的解析式为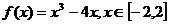 ;
;
②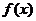 的极值点有且只有一个;
的极值点有且只有一个;
③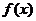 的最大值与最小值之和等于零;
的最大值与最小值之和等于零;
其中正确命题的序号为_ .
15.二项式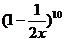 的展开式中含
的展开式中含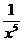 的项的系数是
.
的项的系数是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com