
(二)主要方法:
1.“五点法”画正弦、余弦函数和函数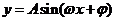 的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
的简图,五个特殊点通常都是取三个平衡点,一个最高、一个最低点;
2.给出图象求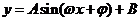 的解析式的难点在于
的解析式的难点在于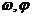 的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期
的确定,本质为待定系数法,基本方法是:①寻找特殊点(平衡点、最值点)代入解析式;②图象变换法,即考察已知图象可由哪个函数的图象经过变换得到的,通常可由平衡点或最值点确定周期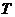 ,进而确定
,进而确定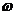 .
.
(一)主要知识:
1.三角函数线:正弦线、余弦线、正切线的作法;
2.函数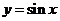 的图象到函数
的图象到函数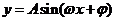 的图象的两种主要途径.
的图象的两种主要途径.
(四)巩固练习:
1.命题“若 不正确,则
不正确,则 不正确”的逆命题的等价命题是 ( )
不正确”的逆命题的等价命题是 ( )
A.若 不正确,则
不正确,则 不正确
B. 若
不正确
B. 若 不正确,则
不正确,则 正确
正确
C 若 正确,则
正确,则 不正确
D. 若
不正确
D. 若 正确,则
正确,则 正确
正确
2.“若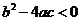 ,则
,则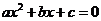 没有实根”,其否命题是 ( )
没有实根”,其否命题是 ( )
A 若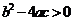 ,则
,则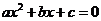 没有实根
没有实根
B 若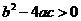 ,则
,则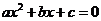 有实根
有实根
C 若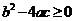 ,则
,则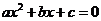 有实根
有实根
D 若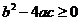 ,则
,则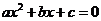 没有实根
没有实根
|

|
版权所有:()
版
(三)例题分析:
例1.指出下列命题的构成形式及构成它的简单命题,并判断复合命题的真假:
(1)菱形对角线相互垂直平分.
(2)“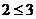 ”
”
解:(1)这个命题是“ 且
且 ”形式,
”形式,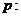 菱形的对角线相互垂直;
菱形的对角线相互垂直;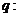 菱形的对角线相互平分,
菱形的对角线相互平分,
∵ 为真命题,
为真命题, 也是真命题 ∴
也是真命题 ∴ 且
且 为真命题.
为真命题.
(2)这个命题是“ 或
或 ”形式,
”形式,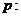
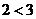 ;
;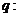
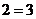 ,
,
∵ 为真命题,
为真命题, 是假命题 ∴
是假命题 ∴ 或
或 为真命题.
为真命题.
注:判断复合命题的真假首先应看清该复合命题的构成形式,然后判断构成它的简单命题的真假,再由真值表判断复合命题的真假.
例2.分别写出命题“若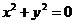 ,则
,则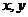 全为零”的逆命题、否命题和逆否命题.
全为零”的逆命题、否命题和逆否命题.
解:否命题为:若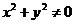 ,则
,则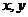 不全为零
不全为零
逆命题:若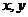 全为零,则
全为零,则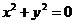
逆否命题:若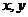 不全为零,则
不全为零,则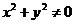
注:写四种命题时应先分清题设和结论.
例3.命题“若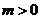 ,则
,则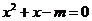 有实根”的逆否命题是真命题吗?证明你的结论.
有实根”的逆否命题是真命题吗?证明你的结论.
解:方法一:原命题是真命题,
∵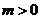 ,∴
,∴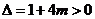 ,
,
因而方程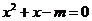 有实根,故原命题“若
有实根,故原命题“若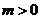 ,则
,则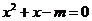 有实根”是真命题;
有实根”是真命题;
又因原命题与它的逆否命题是等价的,故命题“若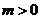 ,则
,则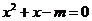 有实根”的逆否命题是真命题.
有实根”的逆否命题是真命题.
方法二:原命题“若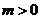 ,则
,则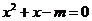 有实根”的逆否命题是“若
有实根”的逆否命题是“若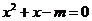 无实根,则
无实根,则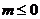 ”.∵
”.∵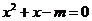 无实根
无实根
∴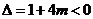 即
即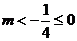 ,故原命题的逆否命题是真命题.
,故原命题的逆否命题是真命题.
例4.(考点6智能训练14题)已知命题 :方程
:方程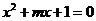 有两个不相等的实负根,命题
有两个不相等的实负根,命题 :方程
:方程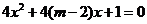 无实根;若
无实根;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数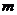 的取值范围.
的取值范围.
分析:先分别求满足条件 和
和 的
的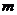 的取值范围,再利用复合命题的真假进行转化与讨论.
的取值范围,再利用复合命题的真假进行转化与讨论.
解:由命题 可以得到:
可以得到: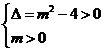 ∴
∴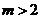
由命题 可以得到:
可以得到: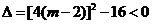 ∴
∴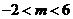
∵ 或
或 为真,
为真, 且
且 为假
为假 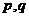 有且仅有一个为真
有且仅有一个为真
当 为真,
为真, 为假时,
为假时,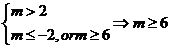
当 为假,
为假, 为真时,
为真时,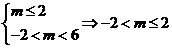
所以,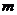 的取值范围为
的取值范围为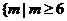 或
或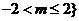 .
.
例5.(《高考A计划》考点5智能训练第14题)已知函数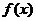 对其定义域内的任意两个数
对其定义域内的任意两个数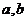 ,当
,当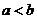 时,都有
时,都有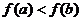 ,证明:
,证明: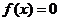 至多有一个实根.
至多有一个实根.
解:假设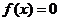 至少有两个不同的实数根
至少有两个不同的实数根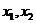 ,不妨假设
,不妨假设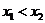 ,
,
由方程的定义可知: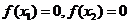
即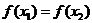
由已知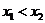 时,有
时,有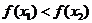 这与式①矛盾
这与式①矛盾
因此假设不能成立
故原命题成立.
注:反证法时对结论进行的否定要正确,注意区别命题的否定与否命题.
例6.(《高考A计划》考点5智能训练第5题)用反证法证明命题:若整数系数一元二次方程: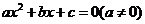 有有理根,那么
有有理根,那么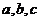 中至少有一个是偶数,下列假设中正确的是( )
中至少有一个是偶数,下列假设中正确的是( )
A.假设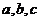 都是偶数
B.假设
都是偶数
B.假设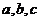 都不是偶数
都不是偶数
C.假设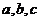 至多有一个是偶数 D.假设
至多有一个是偶数 D.假设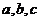 至多有两个是偶数
至多有两个是偶数
(二)主要方法:
1.逻辑联结词“或”“且”“非”与集合中的并集、交集、补集有着密切的关系,解题时注意类比;
2.通常复合命题“ 或
或 ”的否定为“
”的否定为“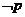 且
且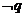 ”、“
”、“ 且
且 ”的否定为“
”的否定为“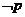 或
或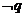 ”、“全为”的否定是“不全为”、“都是”的否定为“不都是”等等;
”、“全为”的否定是“不全为”、“都是”的否定为“不都是”等等;
3.有时一个命题的叙述方式比较的简略,此时应先分清条件和结论,该写成“若 ,则
,则 ”的形式;
”的形式;
4.反证法中出现怎样的矛盾,要在解题的过程中随时审视推出的结论是否与题设、定义、定理、公理、公式、法则等矛盾,甚至自相矛盾.
(一)主要知识:
1.理解由“或”“且”“非”将简单命题构成的复合命题;
2.由真值表判断复合命题的真假;
3.四种命题间的关系.
20.某论坛就“网络能否拉近人们之间的距离”开展了一场辩论,正方认为“网络能够拉近人与人之间的距离”,反方认为“网络疏远了人们之间的关系”。请你分别为正反方各写一段话,证明他们各自的观点。(6分)


正方:
反方:
18. 根据下面一段文字的语境,请将下列五句话按正确顺序排列。( 5分)
大中桥外,顿然空阔,和桥内两岸排着密密的人家的景象大异了。一眼望去,_________________,--这正是秦淮河的夜。
①此地天裸露着的多些,故觉夜来的独迟些;从清清的水影里,我们感到的只是薄薄的夜
②疏疏的林,淡淡的月,衬着蓝蔚的天,颇像荒江野渡光景
③但是河中眩晕着的灯光,纵横着的画舫,悠扬着的笛韵,夹着那吱吱的胡琴声,终于使我们认识绿如茵陈酒的秦淮水了
④那边呢,郁丛丛的,阴森森的,又似乎藏着无边的黑暗
⑤令人几乎不信那是繁华的秦淮河了
答:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com