
3.下列各组中化合物的性质比较,不正确的是( )
A.酸性:HClO4>HBrO4>HIO4 B.碱性:NaOH>Mg(OH)2>Al(OH)3
C.稳定性:PH3>H2S> HCl D.非金属性:F>O>S
2.决定元素种类的是( )
A. 质子数 B电子数. C.中子数 D.质子数和中子数
1.下列有机物中,含有碳碳双键的是( )
A.甲烷 B.乙烯 C.苯 D.乙酸
(四)巩固练习:
1.已知函数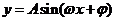 在同一周期内,当
在同一周期内,当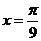 时,取得最大值
时,取得最大值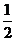 ,当
,当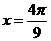 时,取得最小值
时,取得最小值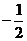 ,则该函数的解析式是
(
,则该函数的解析式是
( 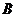 )
)
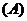
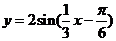
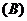
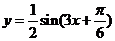
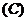
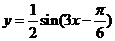
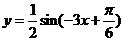
2.若方程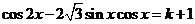 有解,则
有解,则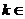
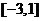 .
.
(三)例题分析:
例1.求函数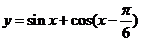 的最大值和最小值.
的最大值和最小值.
解: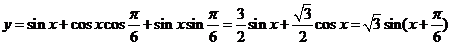 .
.
当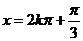 ,
,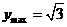 ,当
,当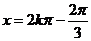 ,
,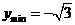
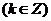 .
.
例2.求函数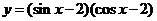 的最大、最小值.
的最大、最小值.
解:原函数可化为: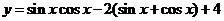 ,
,
令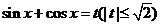 ,
,
则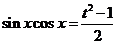 ,∴
,∴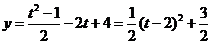 .
.
∵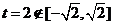 ,且函数在
,且函数在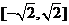 上为减函数,∴当
上为减函数,∴当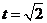 时,即
时,即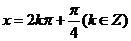 时,
时,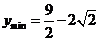 ;当
;当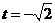 时,即
时,即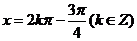 时,
时,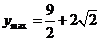 .
.
例3.求下列各式的最值:
(1)已知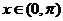 ,求函数
,求函数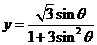 的最大值;
的最大值;
(2)已知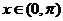 ,求函数
,求函数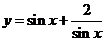 的最小值.
的最小值.
解:(1)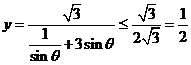 ,当且仅当
,当且仅当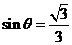 时等号成立.
时等号成立.
故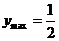 .
.
(2)设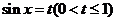 ,则原函数可化为
,则原函数可化为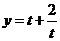 ,在
,在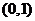 上为减函数,∴当
上为减函数,∴当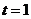 时,
时,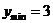 .
.
说明: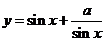 型三角函数求最值,当
型三角函数求最值,当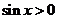 ,
,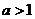 时,不能用均值不等式求最值,适宜用函数在区间内的单调性求解.
时,不能用均值不等式求最值,适宜用函数在区间内的单调性求解.
例4.求函数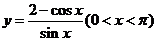 的最小值.
的最小值.
解:原式可化为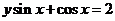
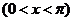 ,引入辅助角
,引入辅助角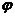 ,
,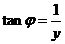 ,得
,得
 ,∴
,∴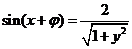 ,由
,由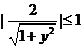 ,
,
得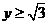 或
或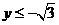 .
.
又∵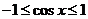 ,∴
,∴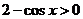 ,且
,且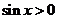 ,故
,故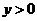 .∴
.∴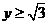 ,故
,故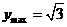 .
.
例5.《高考 计划》考点32,智能训练10:已知
计划》考点32,智能训练10:已知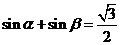 ,则
,则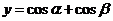 的最大值是 .
的最大值是 .
解:∵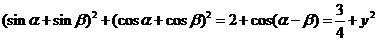 ,
,
∴ ,故当
,故当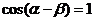 时,
时,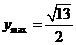 .
.
(二)主要方法:①配方法;②化为一个角的三角函数;③数形结合法;④换元法;⑤基本不等式法.
(一)主要知识:求三角函数的最值,主要利用正、余弦函数的有界性,一般通过三角变换化为下列基本类型处理:
①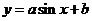 ,设
,设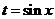 化为一次函数
化为一次函数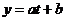 在闭区间
在闭区间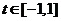 上的最值求之;
上的最值求之;
②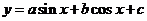 ,引入辅助角
,引入辅助角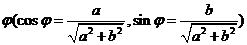 ,化为
,化为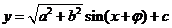 求解方法同类型①;
求解方法同类型①;
③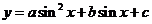 ,设
,设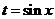 ,化为二次函数
,化为二次函数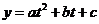 在
在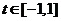 上的最值求之;
上的最值求之;
④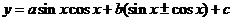 ,设
,设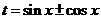 化为二次函数
化为二次函数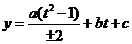 在闭区间
在闭区间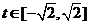 上的最值求之;
上的最值求之;
⑤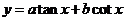 ,设
,设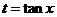 化为
化为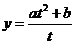 用
用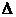 法求值;当
法求值;当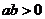 时,还可用平均值定理求最值;
时,还可用平均值定理求最值;
⑥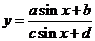 根据正弦函数的有界性,即可分析法求最值,还可“不等式”法或“数形结合”.
根据正弦函数的有界性,即可分析法求最值,还可“不等式”法或“数形结合”.
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.给定映射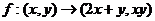 ,点
,点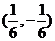 的原象是
的原象是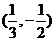 或
或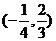 .
.
2.下列函数中,与函数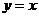 相同的函数是
(
相同的函数是
( 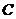 )
)
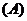
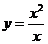
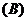
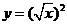
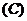
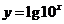
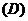
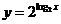
3.设函数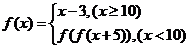 ,则
,则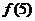 =
=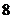 .
.
(三)例题分析:
例1.(1)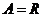 ,
,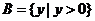 ,
,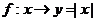 ;
;
(2)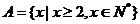 ,
,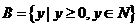 ,
,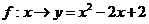 ;
;
(3)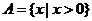 ,
,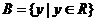 ,
,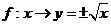 .
.
上述三个对应(2)是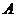 到
到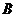 的映射.
的映射.
例2.已知集合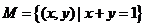 ,映射
,映射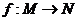 ,在
,在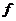 作用下点
作用下点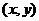 的象是
的象是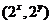 ,则集合
,则集合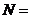 (
( 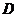 )
)
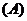
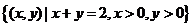
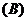
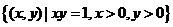
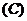
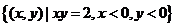
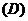
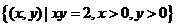
解法要点:因为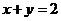 ,所以
,所以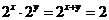 .
.
例3.设集合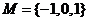 ,
,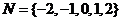 ,如果从
,如果从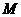 到
到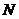 的映射
的映射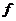 满足条件:对
满足条件:对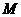 中的每个元素
中的每个元素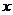 与它在
与它在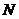 中的象
中的象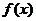 的和都为奇数,则映射
的和都为奇数,则映射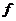 的个数是(
的个数是( 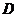 )
)
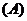 8个
8个 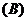 12个
12个  16个
16个  18个
18个
解法要点:∵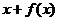 为奇数,∴当
为奇数,∴当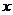 为奇数
为奇数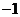 、
、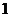 时,它们在
时,它们在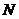 中的象只能为偶数
中的象只能为偶数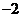 、
、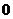 或
或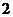 ,由分步计数原理和对应方法有
,由分步计数原理和对应方法有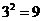 种;而当
种;而当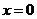 时,它在
时,它在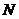 中的象为奇数
中的象为奇数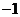 或
或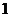 ,共有
,共有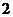 种对应方法.故映射
种对应方法.故映射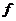 的个数是
的个数是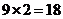 .
.
例4.矩形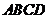 的长
的长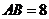 ,宽
,宽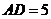 ,动点
,动点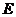 、
、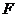 分别在
分别在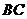 、
、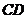 上,且
上,且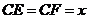 ,(1)将
,(1)将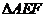 的面积
的面积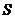 表示为
表示为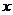 的函数
的函数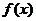 ,求函数
,求函数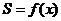 的解析式;
的解析式;
(2)求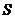 的最大值.
的最大值.
解:(1)
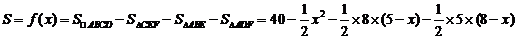
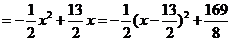 .
.
∵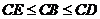 ,∴
,∴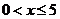 ,
,
∴函数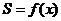 的解析式:
的解析式: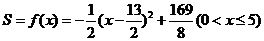 ;
;
(2)∵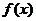 在
在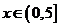 上单调递增,∴
上单调递增,∴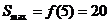 ,即
,即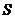 的最大值为
的最大值为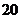 .
.
例5.函数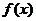 对一切实数
对一切实数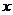 ,
,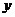 均有
均有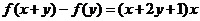 成立,且
成立,且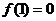 ,
,
(1)求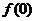 的值;
的值;
(2)对任意的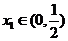 ,
,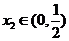 ,都有
,都有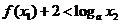 成立时,求
成立时,求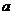 的取值范围.
的取值范围.
解:(1)由已知等式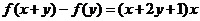 ,令
,令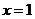 ,
,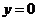 得
得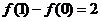 ,
,
又∵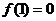 ,∴
,∴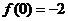 .
.
(2)由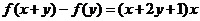 ,令
,令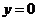 得
得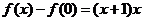 ,由(1)知
,由(1)知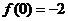 ,∴
,∴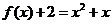 .
.
∵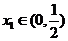 ,∴
,∴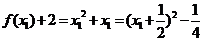 在
在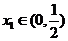 上单调递增,
上单调递增,
∴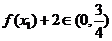 .
.
要使任意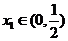 ,
,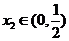 都有
都有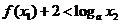 成立,
成立,
当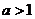 时,
时,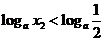 ,显然不成立.
,显然不成立.
当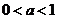 时,
时,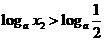 ,∴
,∴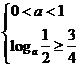 ,解得
,解得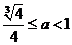
∴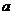 的取值范围是
的取值范围是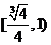 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com