
4.甲、乙两人同时从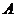 地赶往
地赶往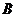 地,甲先骑自行车到中点后改为跑步,而乙则是先跑步到中点后改为骑自行车,最后两人同时到达
地,甲先骑自行车到中点后改为跑步,而乙则是先跑步到中点后改为骑自行车,最后两人同时到达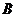 地.又知甲骑自行车比乙骑自行车的速度快,并且两人骑车速度均比跑步速度快.若某人离开
地.又知甲骑自行车比乙骑自行车的速度快,并且两人骑车速度均比跑步速度快.若某人离开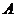 地的距离
地的距离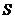 与所用时间
与所用时间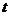 的函数关系可用图①
的函数关系可用图①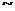 ④中的某一个来表示,则甲、乙两人的图象只可能分别是
④中的某一个来表示,则甲、乙两人的图象只可能分别是
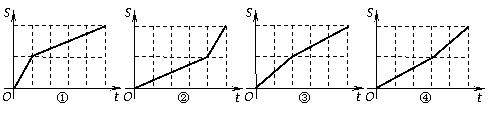
A.甲是图①,乙是图② B.甲是图①,乙是图④
C.甲是图③,乙是图② D.甲是图③,乙是图④
3.已知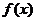 是定义域为
是定义域为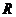 的奇函数,方程
的奇函数,方程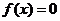 的解集为
的解集为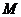 ,且
,且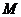 中有有限个元素,则
中有有限个元素,则
A.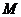 可能是
可能是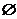 B.
B.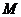 中元素个数是偶数
中元素个数是偶数
C.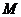 中元素个数是奇数 D.
中元素个数是奇数 D.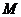 中元素个数可以是偶数,也可以是奇数
中元素个数可以是偶数,也可以是奇数
2.函数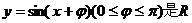 上的偶函数,则
上的偶函数,则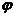 =
=
A.0 B.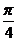 C.
C.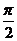 D.
D.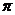
1.已知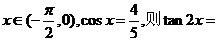
A.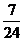 B.
B.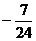 C.
C.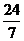 D.
D.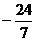
|

|
(四)巩固练习:
1.已知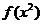 的定义域为
的定义域为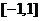 ,则
,则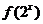 的定义域为
的定义域为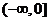 .
.
2.函数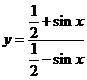 的定义域为
的定义域为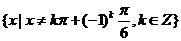 .
.
(三)例题分析:
例1.已知函数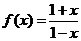 的定义域为
的定义域为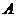 ,函数
,函数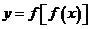 的定义域为
的定义域为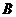 ,则
,则
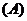
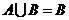
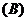
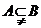
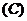
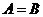
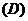
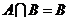 (
( 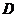 )
)
解法要点: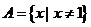 ,
,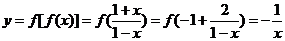 ,
,
令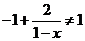 且
且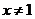 ,故
,故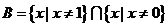 .
.
例2.(1)已知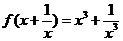 ,求
,求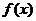 ;
;
(2)已知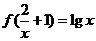 ,求
,求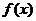 ;
;
(3)已知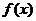 是一次函数,且满足
是一次函数,且满足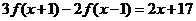 ,求
,求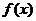 ;
;
(4)已知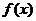 满足
满足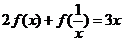 ,求
,求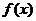 .
.
解:(1)∵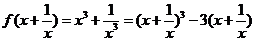 ,
,
∴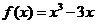 (
(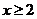 或
或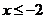 ).
).
(2)令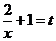 (
(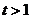 ),
),
则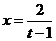 ,∴
,∴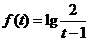 ,∴
,∴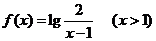 .
.
(3)设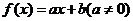 ,
,
则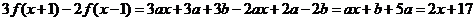 ,
,
∴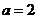 ,
,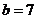 ,∴
,∴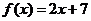 .
.
(4)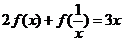 ①,把①中的
①,把①中的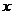 换成
换成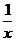 ,得
,得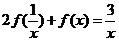 ②,
②,
①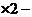 ②得
②得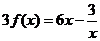 ,∴
,∴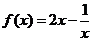 .
.
注:第(1)题用配凑法;第(2)题用换元法;第(3)题已知一次函数,可用待定系数法;第(4)题用方程组法.
例3.设函数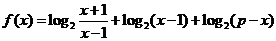 ,
,
(1)求函数的定义域;
(2)问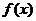 是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由.
是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由.
解:(1)由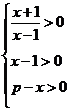 ,解得
,解得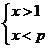 ①
①
当 时,①不等式解集为
时,①不等式解集为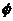 ;当
;当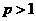 时,①不等式解集为
时,①不等式解集为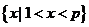 ,
,
∴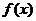 的定义域为
的定义域为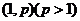 .
.
(2)原函数即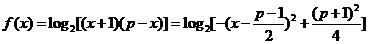 ,
,
当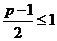 ,即
,即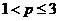 时,函数
时,函数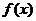 既无最大值又无最小值;
既无最大值又无最小值;
当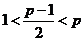 ,即
,即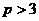 时,函数
时,函数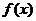 有最大值
有最大值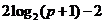 ,但无最小值.
,但无最小值.
例4.《高考 计划》考点8,智能训练15:已知函数
计划》考点8,智能训练15:已知函数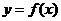 是定义在
是定义在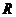 上的周期函数,周期
上的周期函数,周期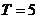 ,函数
,函数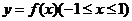 是奇函数.又知
是奇函数.又知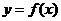 在
在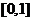 上是一次函数,在
上是一次函数,在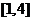 上是二次函数,且在
上是二次函数,且在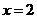 时函数取得最小值
时函数取得最小值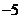 .
.
①证明: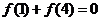 ;②求
;②求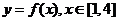 的解析式;③求
的解析式;③求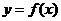 在
在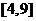 上的解析式.
上的解析式.
解:∵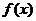 是以
是以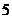 为周期的周期函数,∴
为周期的周期函数,∴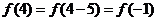 ,
,
又∵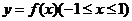 是奇函数,∴
是奇函数,∴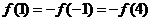 ,
,
∴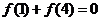 .
.
②当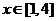 时,由题意可设
时,由题意可设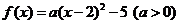 ,
,
由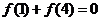 得
得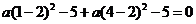 ,∴
,∴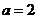 ,
,
∴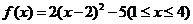 .
.
③∵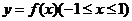 是奇函数,∴
是奇函数,∴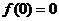 ,
,
又知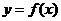 在
在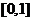 上是一次函数,∴可设
上是一次函数,∴可设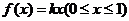 ,而
,而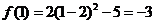 ,
,
∴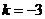 ,∴当
,∴当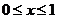 时,
时,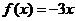 ,
,
从而当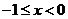 时,
时,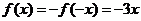 ,故
,故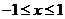 时,
时,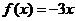 .
.
∴当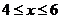 时,有
时,有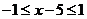 ,∴
,∴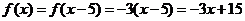 .
.
当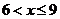 时,
时,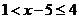 ,∴
,∴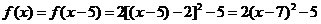
∴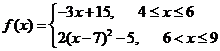 .
.
例5.我国是水资源比较贫乏的国家之一,各地采取价格调控等手段来达到节约用水的目的,某地用水收费的方法是:水费=基本费+超额费+损耗费.若每月用水量不超过最低限量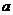
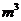 时,只付基本费8元和每月每户的定额损耗费
时,只付基本费8元和每月每户的定额损耗费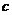 元;若用水量超过
元;若用水量超过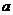
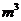 时,除了付同上的基本费和定额损耗费外,超过部分每
时,除了付同上的基本费和定额损耗费外,超过部分每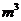 付
付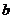 元的超额费.已知每户每月的定额损耗费不超过5元.
元的超额费.已知每户每月的定额损耗费不超过5元.
该市一家庭今年第一季度的用水量和支付费如下表所示:
|
月份 |
用水量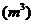 |
水费(元) |
|
1 2 3 |
9 15 22 |
9 19 33 |
根据上表中的数据,求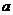 、
、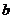 、
、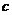 .
.
解:设每月用水量为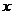
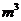 ,支付费用为
,支付费用为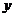 元,则有
元,则有

由表知第二、第三月份的水费均大于13元,故用水量15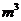 ,22
,22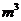 均大于最低限量
均大于最低限量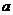
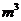 ,于是就有
,于是就有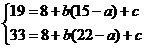 ,解之得
,解之得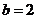 ,从而
,从而
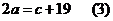
再考虑一月份的用水量是否超过最低限量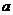
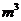 ,不妨设
,不妨设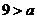 ,将
,将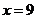 代入(2)式,得
代入(2)式,得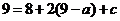 ,即
,即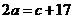 ,这与(3)矛盾.∴
,这与(3)矛盾.∴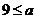 .
.
从而可知一月份的付款方式应选(1)式,因此,就有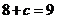 ,得
,得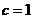 .
.
故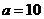 ,
,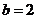 ,
,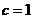 .
.
(二)主要方法:
1.求函数解析式的题型有:
(1)已知函数类型,求函数的解析式:待定系数法;
(2)已知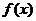 求
求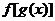 或已知
或已知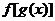 求
求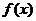 :换元法、配凑法;
:换元法、配凑法;
(3)已知函数图像,求函数解析式;
(4)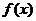 满足某个等式,这个等式除
满足某个等式,这个等式除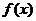 外还有其他未知量,需构造另个等式:解方程组法;
外还有其他未知量,需构造另个等式:解方程组法;
(5)应用题求函数解析式常用方法有待定系数法等.
2.求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知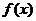 的定义域求
的定义域求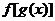 的定义域或已知
的定义域或已知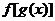 的定义域求
的定义域求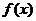 的定义域:
的定义域:
①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域;
②若已知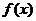 的定义域
的定义域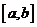 ,其复合函数
,其复合函数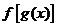 的定义域应由
的定义域应由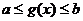 解出.
解出.
(一)主要知识:1.函数解析式的求解;2.函数定义域的求解.
45、(6分)根据下图,回答下列问题:



(1)此图解全过程叫 。
(2)图中③的重理过程叫 ;该过程需要在 的作用下才能进行。
(3)图中④的生理过程叫RNA复制;该过程的发现,说明RNA也可作为生物的 。
(4)从DNA的功能看,图中①过程属于DNA的
功能;图中②和⑤过程属于DNA的
功能。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com