
20. 已知在数列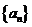 中,
中, ,且点
,且点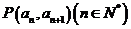 在直线
在直线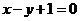 上。
上。
(1)求数列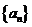 的通项公式;
的通项公式;
(2)若函数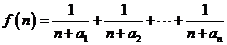
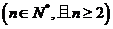 ,求函数
,求函数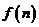 的最小值。
的最小值。
(3)若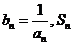 表示数列
表示数列 的前
的前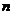 项和,试问:是否存在关于
项和,试问:是否存在关于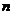 的整式
的整式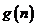 ,使得
,使得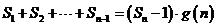 对一切
对一切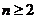 的自然数
的自然数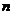 恒成立?若存在,写出
恒成立?若存在,写出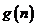 的解析式并证明,若不存在,请说明理由。
的解析式并证明,若不存在,请说明理由。




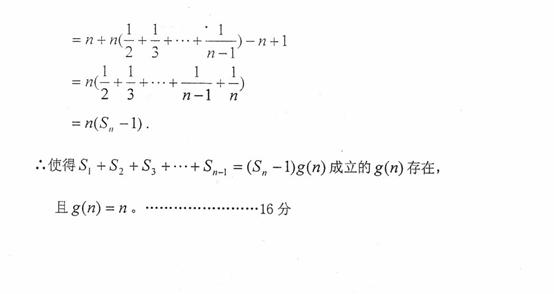


19、(本小题满分16分)
已知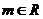 ,函数
,函数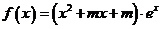 。
。
(I)若函数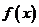 没有零点,求实数
没有零点,求实数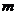 的取值范围;
的取值范围;
(II)若函数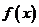 存在极大值,并记为
存在极大值,并记为 ,求
,求 的表达式;
的表达式;
(III)当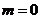 时,求证:
时,求证: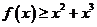 。
。
18. 某国由于可耕地面积少,计划从今年起的五年填湖围造一部分生产和生活用地,若填湖飞、购置排水设备费等所需经费与当年所填湖造地面积 (亩)的平方成长正比,其比例系数为
(亩)的平方成长正比,其比例系数为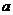 ,设每亩水面的年平均经济效益为
,设每亩水面的年平均经济效益为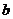 元,填湖造地后的每亩土地的年平均收益为
元,填湖造地后的每亩土地的年平均收益为 元(其中
元(其中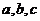 均为常数,且
均为常数,且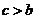 )
)
(1)若按计划填湖造地,且使得今年的收益不少于支出,试求所填面积 的最大值;(支出=造田的所需经费+水面经济收益)
的最大值;(支出=造田的所需经费+水面经济收益)
(2)如果填湖造地面积按每年1%的速度减少,为保证水面的蓄洪能力和环保要求,填湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几。
注:根据下列近似值进行计算:
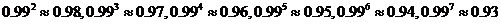
17、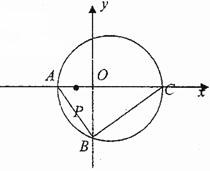 如图,直角三角形
如图,直角三角形 的顶点坐标
的顶点坐标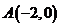 ,直角顶点
,直角顶点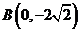 ,顶点
,顶点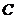 在
在 轴上,点
轴上,点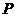 为线段
为线段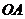 的中点。
的中点。
(1)求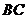 边所在直线方程;
边所在直线方程;
(2)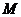 为直角三角形
为直角三角形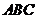 外接圆的圆心,求圆
外接圆的圆心,求圆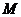 的方程;
的方程;
(3)若动圆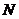 多点
多点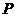 且与圆
且与圆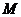 内切,求动圆
内切,求动圆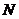 的圆心
的圆心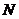 的轨迹。
的轨迹。
16、(本小题满分14分)
在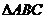 中,角
中,角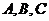 的对边分别为
的对边分别为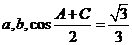 。
。
(1)求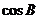 的值;
的值;
(2)若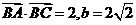 ,求
,求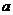 和
和 的值。
的值。
15、(本小题满分14分)
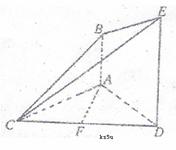 如图,已知
如图,已知 平面
平面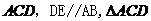 是正三角形,
是正三角形,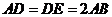 ,且
,且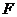 是
是 的中点。
的中点。
(I)求证: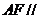 平面
平面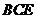 ;
;
(II)求证:平面 平面
平面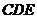 ;
;
14. 函数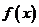 的定义域为
的定义域为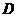 ,若满足①
,若满足①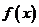 在
在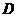 内是单调函数,②存在
内是单调函数,②存在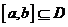 ,使
,使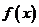 在
在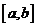 上的值域为
上的值域为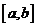 ,那么
,那么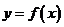 叫做闭函数,现有
叫做闭函数,现有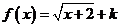 是闭函数,那么
是闭函数,那么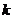 的取值范围是
。
的取值范围是
。
13. 已知直线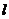 的方程为
的方程为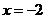 ,圆
,圆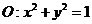 则以
则以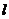 为准线,中心在原点,且与圆
为准线,中心在原点,且与圆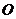 恰好有两个公共点的椭圆方程为
;
恰好有两个公共点的椭圆方程为
;
12. 设函数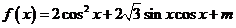 且
且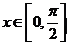 ,若函数
,若函数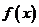 的值域恰为
的值域恰为
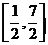 ,则实数
,则实数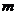 的值为
。
的值为
。
11. 正方体的八个顶点中有四个恰好为正四面体的顶点,则正
方体的全面积与正四面体的全面积之比为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com