
21.解:(Ⅰ)2b=2.b=1,e=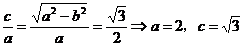
椭圆的方程为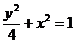 ………………………4分
………………………4分
(Ⅱ)(1)当直线AB斜率不存时,即x1=x2,y1= -y2,由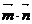 =0
=0
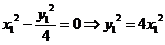 ………………………6分
………………………6分
又A(x1,y1)在椭圆上,所以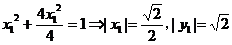
S=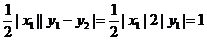
所以三角形的面积为定值 ………………………7分
(2)当直线AB斜率存在时,设AB的方程为y=kx+b
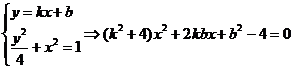 得到x1+ x1=
得到x1+ x1=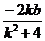
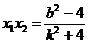 ………………………8分
………………………8分
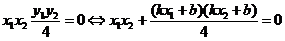 代入整理得:
代入整理得:
2b2- k2 =4 ………………………10分
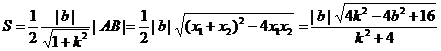
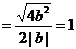
所以三角形的面积为定值. ……………………12分
20.解:(1)解: ∵ 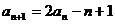 , ∴
, ∴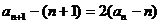 ,
,
∴ 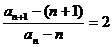 , 又
, 又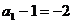 ,
,
∴ 数列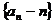 是以2为公比、以-2为首项的等比数列.…………… 6分
是以2为公比、以-2为首项的等比数列.…………… 6分
(2)由(1)得: 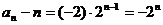 , ∴
, ∴ 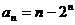 ,
,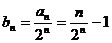 ,
,
∴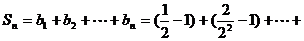
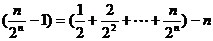 ,
,
令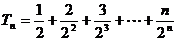 , 则
, 则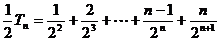 ,
,
两式相减得: 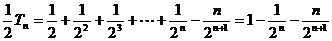
∴ 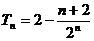 , 即
, 即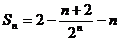 . ………………………12分
. ………………………12分
19.(解:(Ⅰ)选择①②作为条件.……………………………………………… 1分
证明如下:∵PA=AD=1,PD=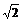 ∴
∴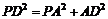 ∴∠PAD=
∴∠PAD=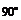 ,即PA⊥AD
,即PA⊥AD
同理,可证PA⊥AB ∴PA⊥平面ABCD ∴PA⊥CD K^S*5U.
∵四边形ABCD是正方形,∴AD⊥CD ………………………………………… 4分
∴CD⊥平面PAD ………………………………………………………………… 5分
又CD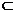 平面PCD,∴平面PCD⊥平面PAD.………………………………… 6分
平面PCD,∴平面PCD⊥平面PAD.………………………………… 6分
(Ⅱ)∵PA⊥平面ABCD ∴PA⊥AB,PA⊥AD,
∵CD⊥平面PAD ∴CD⊥PD,同理有BC⊥PB
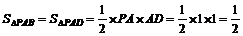
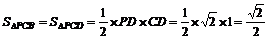 ,
,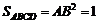 …………… 10分
…………… 10分
∴在四棱锥P-ABCD的表面上任取一个点,这个点在四棱锥P-ABCD侧面内的概率是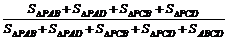
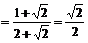 .………………………… 12分
.………………………… 12分
(注:选择②③也是正确的,其余选择都是错误的.)
18.(本小题满分12分)
解:(Ⅰ)由题意得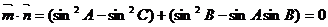
即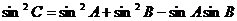 --------------------------2分
--------------------------2分
由正弦定理得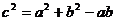 --------------------------3分
--------------------------3分
再由余弦定理得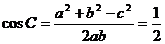
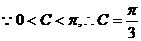 --------------------------5分
--------------------------5分
(Ⅱ)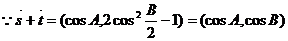 --------------------------6分
--------------------------6分
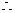
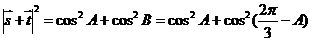
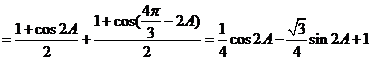 -----------------------8分
-----------------------8分
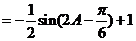 --------------------------10分
--------------------------10分
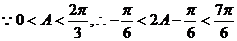
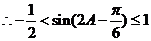
所以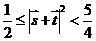 ,故
,故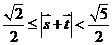 . --------
. --------
17.解:(Ⅰ)棋子3次跳动的所有路径如下:
AàBàCàA,AàBàCàB,AàBàAàB,AàBàAàC
AàCàBàA,AàCàBàC,AàCàAàC,AàCàAàB
共8条路径. ………………………………………………………………… 8分
(Ⅱ)记“3次跳动后,棋子停在A点”为事件A,
则事件A包含2个基本事件:AàBàCàA,AàCàBàA.………………… 10分
∴P(A)=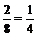
即3次跳动后,棋子停在A点的概率为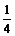 .…………………………………… 12分
.…………………………………… 12分
13.60 14. 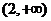 15.
(2) (3) (4) 16.
15.
(2) (3) (4) 16. 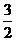
22. (本题满分14分)
已知函数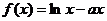 .
.
(Ⅰ)求函数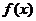 的极值,
的极值,
(Ⅱ)已知过点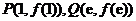 的直线为
的直线为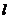 ,则必存在
,则必存在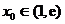 ,使曲线
,使曲线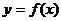 在点
在点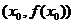 处的切线与直线
处的切线与直线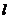 平行,求
平行,求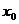 的值,
的值,
(Ⅲ)将(2)的结论推广为:若函数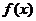 图象在
图象在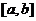 上连续不断,且
上连续不断,且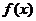 在
在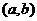 内存在导函数,则必存在
内存在导函数,则必存在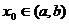 ,使
,使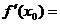 __①__。(求出答案)
__①__。(求出答案)
已知函数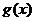 图象在
图象在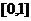 上连续不断,且函数
上连续不断,且函数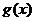 的导函数
的导函数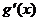 在区间
在区间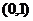 内单调递减,若
内单调递减,若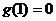 ,试用上述结论证明:对于任意
,试用上述结论证明:对于任意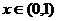 ,恒有
,恒有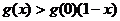 成立.
成立.
2010年安溪八中高三数学最后一次模拟试卷(文科)
DADCDD BBBDAC
21.(本题满分12分)
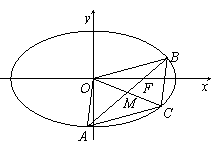 设A(x1,y1),B(x2,y2),是椭圆
设A(x1,y1),B(x2,y2),是椭圆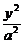 +
+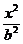 =(a>b>0)上的两点,已知向量m=(
=(a>b>0)上的两点,已知向量m=(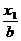 ,
,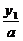 ),n=(
),n=(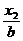 ,
,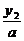 ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=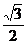 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由..
20.(本题满分12分)
在数列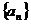 中,已知
中,已知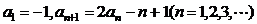 .
.
(1)证明数列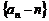 是等比数列;
是等比数列;
(2) 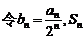 为数列
为数列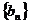 的前
的前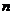 项和,求
项和,求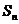 的表达式. 高
的表达式. 高
19.如图,四棱锥P-ABCD中,PA=AB=AD=1.
(Ⅰ)请你在下面四个选项中选择2个作为条件,使得能推出平面PCD⊥平面PAD,并证明.
①PB=PD=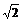 ; ②四边形ABCD是正方形;
; ②四边形ABCD是正方形;
③PA⊥平面ABCD; ④平面PAB⊥平面ABCD.
(Ⅱ)在(Ⅰ)选择的条件下,在四棱锥P-ABCD的表面上任取一个点,求这个点在四棱锥P-ABCD侧面内的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com