
例1.比较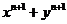 和
和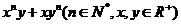 的大小.
的大小.
例2.设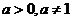 ,
,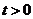 ,比较
,比较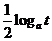 和
和
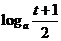 的大小,并证明你的结论.
的大小,并证明你的结论.
例3.在等比数列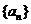 与等差数列
与等差数列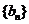 中,
中,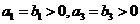 ,且
,且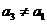 ,
,
比较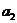 与
与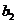 ,
,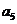 与
与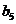 的大小.
的大小.
例4.设数列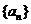 的通项公式是
的通项公式是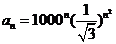 ,
,
(1)讨论数列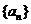 的单调性;(2)求数列中的最大项.
的单调性;(2)求数列中的最大项.
3.如果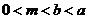 ,则 ( )
,则 ( )
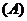
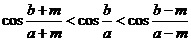
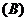
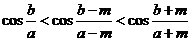
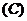
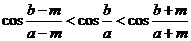
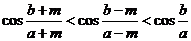 .
.
2.已知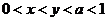 ,则 ( )
,则 ( )
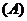
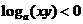
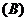
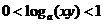
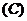
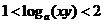
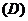
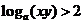 .
.
1.命题(1)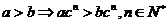 ,(2)
,(2)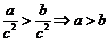 ,(3)
,(3)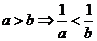 ,
,
(4)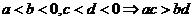 ,(5)
,(5)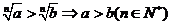
(6)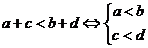 ,(7)
,(7)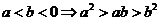
其中真命题的是 .
2.比较两数大小的一般方法是: .
1.不等式的性质:①对称性: ;②传递性: .
③加法性质; .
④乘法性质: , .
⑤乘方性质: ;开方性质 .
2.掌握比较两个实数大小的一般步骤.
1.掌握并能运用不等式的性质,灵活运用实数的性质;
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.若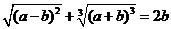 ,则
,则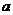 与
与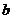 的大小关系为
;
的大小关系为
;
2.若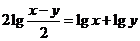 ,求
,求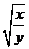 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com