
2.换元法:一般由代数式的整体换元、三角换元,换元时要注意等价性;
1.反证法的一般步骤:反设--推理--导出矛盾(得出结论);
1.了解用反证法、换元法、放缩法等方法证明简单的不等式.
|

|
(四)巩固练习:
1.函数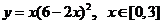 的最大值为 16 ;
的最大值为 16 ;
2.若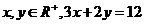 ,则
,则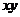 的最大值是 6 ;
的最大值是 6 ;
3.若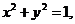 则
则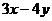 的最小值是
的最小值是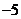 ;
;
4.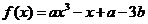 ,
, 在
在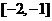 和
和 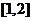 上是单调递减函数,则
上是单调递减函数,则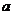 的最大值为
的最大值为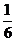 .
.
(三)例题分析:
例1.求下列函数的最大值或最小值:
(1) 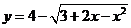 ;(2)
;(2)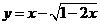 ;(3)
;(3)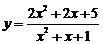 .
.
解:(1)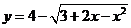
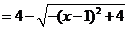 ,由
,由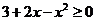 得
得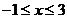 ,
,
∴当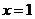 时,函数取最小值
时,函数取最小值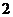 ,当
,当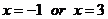 时函数取最大值
时函数取最大值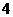 .
.
(2)令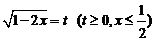 ,则
,则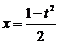 ,∴
,∴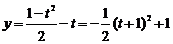 ,
,
当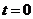 ,即
,即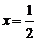 时取等号,∴函数取最大值
时取等号,∴函数取最大值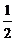 ,无最小值.
,无最小值.
(3)解法(一)用判别式法:
由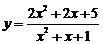 得
得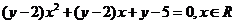 ,
,
①若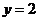 ,则
,则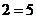 矛盾, ∴
矛盾, ∴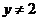 ,
,
②由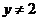 ,这时,
,这时,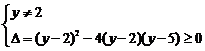 ,解得:
,解得: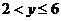 ,
,
且当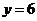 时,
时,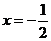 , ∴函数的最大值是
, ∴函数的最大值是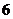 ,无最小值.
,无最小值.
解法(二)分离常数法:
由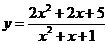
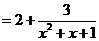
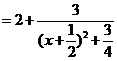
∵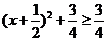 ,∴
,∴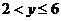 ,∴函数的最大值是
,∴函数的最大值是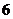 ,无最小值.
,无最小值.
例2.(1)函数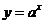 在
在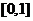 上的最大值与最小值的和为
上的最大值与最小值的和为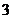 ,则
,则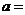 2 .
2 .
(2)对于满足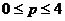 的一切实数,不等式
的一切实数,不等式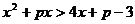 恒成立,则
恒成立,则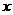 的取值范围为
的取值范围为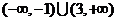 .
.
(3)已知函数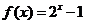 ,
,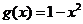 ,构造函数
,构造函数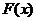 ,定义如下:当
,定义如下:当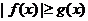 时,
时,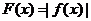 ,当
,当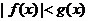 时,
时,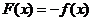 ,那么
,那么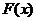
( 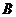 )
)
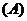 有最小值
有最小值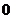 ,无最大值
,无最大值
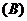 有最小值
有最小值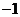 ,无最大值
,无最大值
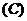 有最大值
有最大值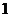 ,无最小值
,无最小值
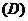 无最小值,也无最大值
无最小值,也无最大值
例3.(《高考 计划》考点17“智能训练第14题”)已知
计划》考点17“智能训练第14题”)已知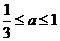 ,若
,若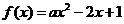 在
在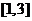 上的最大值为
上的最大值为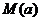 ,最小值为
,最小值为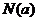 ,令
,令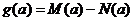 ,
,
(1)求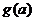 的函数表达式; (2)判断函数
的函数表达式; (2)判断函数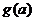 的单调性,并求出
的单调性,并求出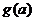 的最小值.
的最小值.
答案参看教师用书 .
.
(二)主要方法:
1.函数的最值问题实质上是函数的值域问题,因此求函数值域的方法,也是求函数的值域的方法,只是答题的方式有所差异;
2.无论用什么方法求最值,都要考查“等号”是否成立,不等式法及判别式法尤其如此.
(一)主要知识:
1.函数最值的意义;
2.求函数最值的常用方法:(1)配方法:主要适用于可化为二次函数或可化为二次函数的函数,要特别注意自变量的范围;(2)判别式法:主要适用于可化为关于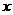 的二次方程
的二次方程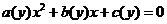 的函数
的函数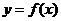 .在由
.在由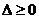 且
且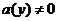 ,求出
,求出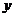 的值后,要检验这个最值在定义域内是否有相应的
的值后,要检验这个最值在定义域内是否有相应的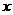 的值;(3)不等式法:利用基本不等式求最值时一定要注意应用的条件;(4)换元法:用换元法时一定要注意新变元的取值范围;(5)数形结合法:对于图形较容易画出的函数的最值问题可借助图象直观求出;(6)利用函数的单调性:要注意函数的单调性对函数最值的影响,特别是闭区间上函数的最值.
的值;(3)不等式法:利用基本不等式求最值时一定要注意应用的条件;(4)换元法:用换元法时一定要注意新变元的取值范围;(5)数形结合法:对于图形较容易画出的函数的最值问题可借助图象直观求出;(6)利用函数的单调性:要注意函数的单调性对函数最值的影响,特别是闭区间上函数的最值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com